算法笔记--散列
1、散列函数的构造方法(浙大数据结构)
一个“好”的散列函数一般应考虑下列两个因素:
- 计算简单,以便提高转换速度;
- 关键词对应的地址空间分布均匀,以尽量减少冲突。
1 数字关键词的散列函数构造
1.1 直接定址法
取关键词的某个线性函数值为散列地址,即
h(key) = a × key + b (a、b为常数)
地址 h(key) | 出生年月(key) | 人数(attribute) |
|---|---|---|
| 0 | 1900 | 1285万 |
| 1 | 1901 | 1281万 |
| 2 | 1902 | 1280万 |
| …… | …… | …… |
| 10 | 2000 | 1250万 |
| …… | …… | …… |
| 10 | 2011 | 1180万 |
根据上表,得出散列函数的构造函数为:h(key)=key-1990
1.2 除留余数法
散列函数为:h( key ) = key mod p
例: h( key ) = key % 17
| 地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 关键词 | 34 | 18 | 2 | 20 | 23 | 7 | 42 | 27 | 11 | 30 |
15 |
一般,p 取素数,这里:p = Tablesize = 17
1.3 数字分析法
分析数字关键字在各位上的变化情况,取比较随机的位作为散列地址
比如:取11位手机号码key的后4位作为地址:
散列函数为:h(key) = atoi(key+7) (char *key)
如果关键词 key是18位的身份证号码: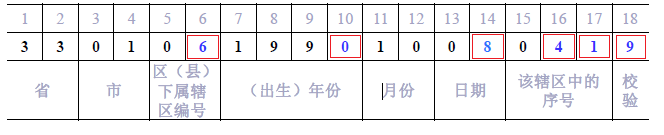
用红线标出来的是变化比较大的的6位数字,这里就取这6位数字来组建散列函数
h1(key) = (key[6]-‘0’)×104 + (key[10]-‘0’)×103 +(key[14]-‘0’)×102 + (key[16]-‘0’)×101 + (key[17]-‘0’)
当 key[18] = ‘x’时(字母)
h(key) = h1(key)×10 + 10
当 key[18] 为’0’~’9’时,身份证最后一位为数字
h(key) = h1(key)×10 + key[18]-‘ 0 ’
1.4 折叠法
把关键词分割成位数相同的几个部分,然后叠加
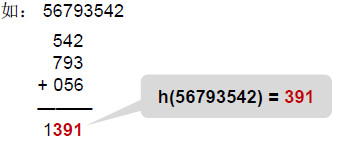
1.5 平方取中法
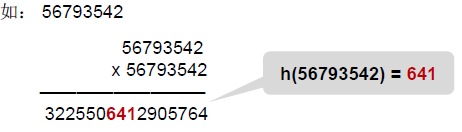
2、字符关键词的散列函数构造
2.1 一个简单的散列函数——ASCII码加和法
对字符型关键词key定义散列函数如下:
h(key) = ( Σkey[i] ) mod TableSize
问题:对于ASCII之和相同的字符串就会冲突,比如a3、 b2、c1;eat、 tea;
2.2 简单的改进——前3个字符移位法
把字符串的前三个字符取出来,看成27进制种的个位数,十位数,百位数,为什么使用27,因为有26个字符,考录空格,就是27。
h(key)=(key[0]×272 + key[1]×271 + key[2]) mod TableSize
问题:
1、仍然冲突:string、 street、strong、structure等等,前三个字符相同;
2、空间浪费:3000/263 ≈ 30%
前三个字符的不同组合在实际使用中大概有3000种可能,我们假设所有的字母(26个英文字母)排列组合有263种情况,散列表只用到30%。
2.3 好的散列函数——移位法
涉及关键词所有n个字符,并且分布得很好:
这里就考虑这个字符串的所有位。把它看成是32进制数的每一位
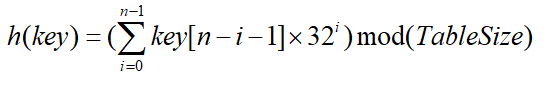
h(“abcde”)=‘a’*324+’b’*323+’c’*322+’d’*321+’e’
计算过程如下:
h = a
h = a * 32 + b
h = (a * 32 +b) * 32 + c
h = ((a * 32 + b) * 32 + c) * 32 + d
h = (((a * 32 + b) * 32 + c) * 32 + d) * 32 + e
h = h % TableSize
这里a * 32 == a<<5,左移5位相当于乘以32
快速计算代码如下:
Index Hash(const char *Key, int TableSize)
{
unsigned int h = 0; //散列函数值,初始化为0
while (*Key != '\0') //位移映射
h = (h << 5) + *Key++;
return h % TableSize;
}
3、碰撞处理方法
1)开放定址法

(1)线性探测法
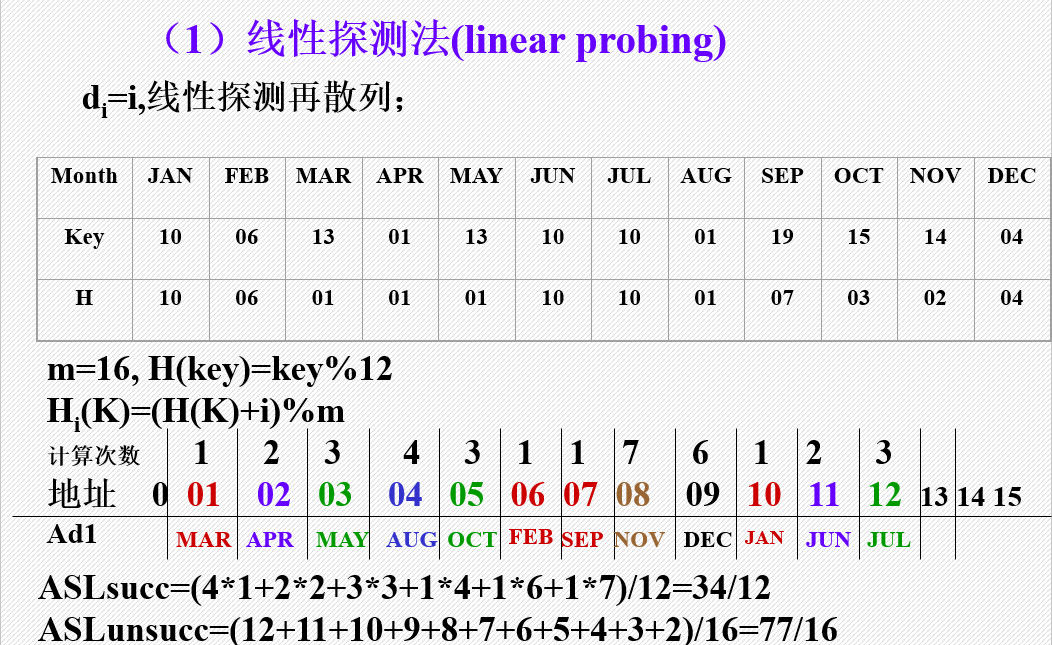
(2)平方探测法
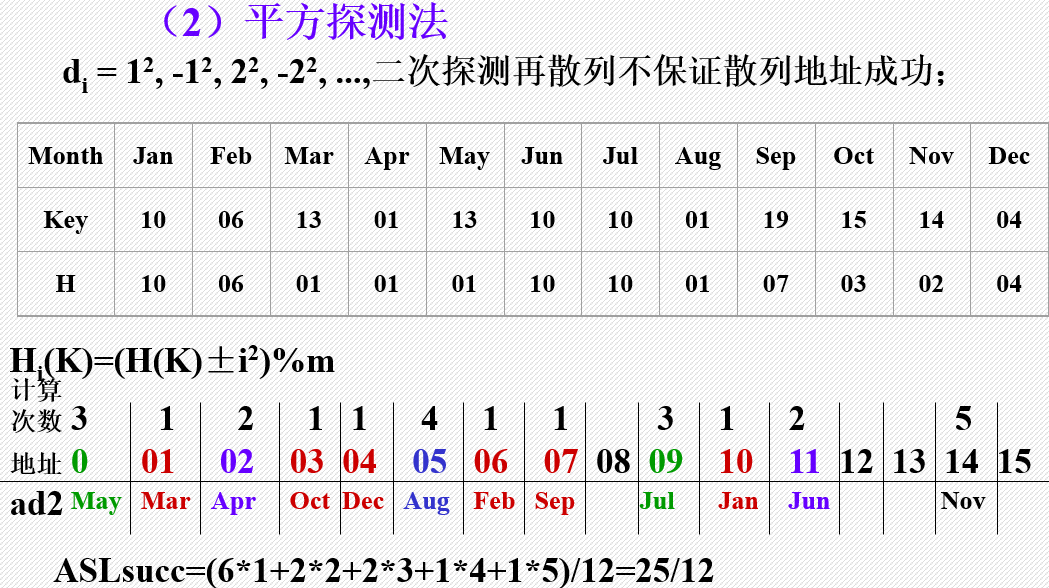
(3)伪随机数探测法

2)再散列

3)链地址法
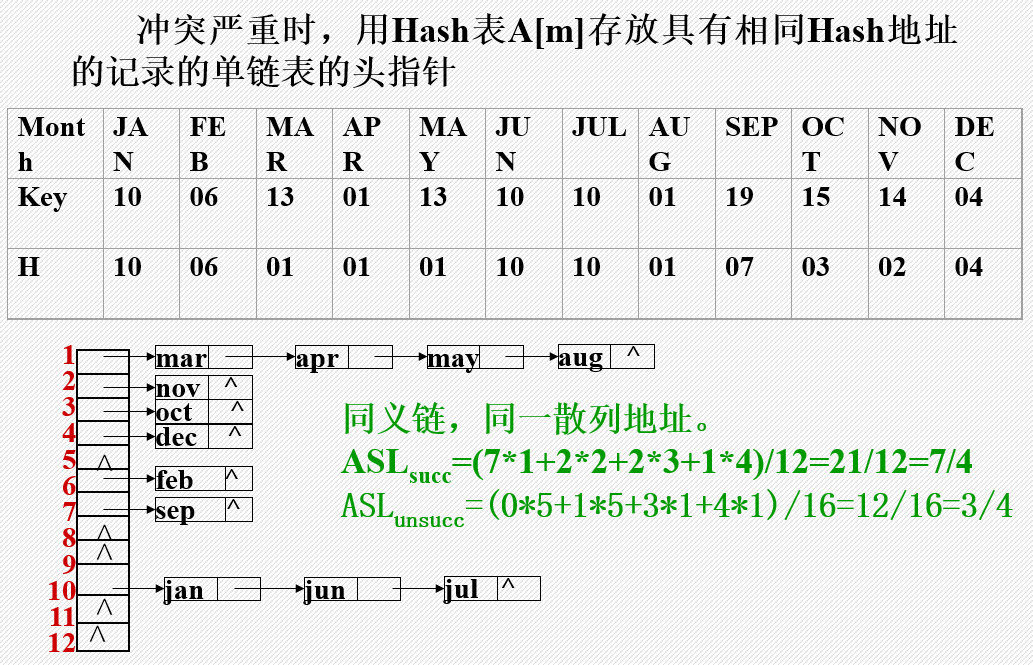
4)建立一个公共溢出表

4、例题
Q:给出N个字符串(由恰好三位大写字符组成),再给出M个查询字符串,问每个查询字符串在N个字符串中出现的次数
#include<cstdio>
#include<cstring>
int Char2Int(char s[], int len){
int id = 0;
for(int i=0; i < len; i++){
id = id * 26 + ( s[i] - 'A' );
}
return id;
}
int main(){
int n, m;
int hashTable[26 * 26 * 26 + 10] = {0};
char N[5], M[5];
printf("输入字符串个数:");
scanf("%d\n", &n);
for(int i=0; i < n; i++){
scanf("%s", N);
int j = Char2Int(N, 3);
hashTable[j] ++;
}
printf("输入查询字符串个数:");
scanf("%d\n", &m);
for(int i=0; i < m; i++){
scanf("%s", M);
int k = Char2Int(M, 3);
printf("%d\n", hashTable[k]);
}
return 0;
}
结果:
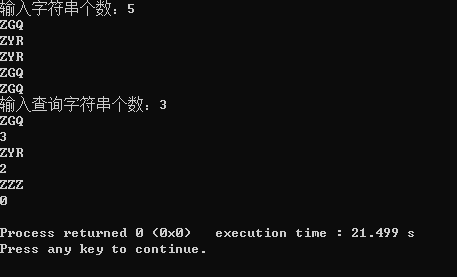


 浙公网安备 33010602011771号
浙公网安备 33010602011771号