GMM的EM算法实现
在 聚类算法K-Means, K-Medoids, GMM, Spectral clustering,Ncut一文中我们给出了GMM算法的基本模型与似然函数,在EM算法原理中对EM算法的实现与收敛性证明进行了具体说明。本文主要针对怎样用EM算法在混合高斯模型下进行聚类进行代码上的分析说明。
1. GMM模型:
每一个 GMM 由 K 个 Gaussian 分布组成,每一个 Gaussian 称为一个“Component”,这些 Component 线性加成在一起就组成了 GMM 的概率密度函数:
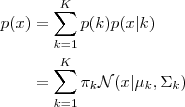
依据上面的式子,如果我们要从 GMM 的分布中随机地取一个点的话,实际上能够分为两步:首先随机地在这 K个Gaussian Component 之中选一个,每一个 Component 被选中的概率实际上就是它的系数 pi(k) ,选中了 Component 之后,再单独地考虑从这个 Component 的分布中选取一个点就能够了──这里已经回到了普通的 Gaussian 分布,转化为了已知的问题。
那么怎样用 GMM 来做 clustering 呢?事实上非常简单,如今我们有了数据,假定它们是由 GMM 生成出来的,那么我们仅仅要依据数据推出 GMM 的概率分布来就能够了,然后 GMM 的 K 个 Component 实际上就相应了 K 个 cluster 了。依据数据来推算概率密度通常被称作 density estimation ,特别地,当我们在已知(或假定)了概率密度函数的形式,而要预计当中的參数的过程被称作“參数预计”。
2. 參数与似然函数:
如今如果我们有 N 个数据点,并如果它们服从某个分布(记作 p(x) ),如今要确定里面的一些參数的值,比如,在 GMM 中,我们就须要确定 影响因子pi(k)、各类均值pMiu(k) 和 各类协方差pSigma(k) 这些參数。 我们的想法是,找到这样一组參数,它所确定的概率分布生成这些给定的数据点的概率最大,而这个概率实际上就等于 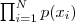 ,我们把这个乘积称作似然函数 (Likelihood Function)。通常单个点的概率都非常小,很多非常小的数字相乘起来在计算机里非常easy造成浮点数下溢,因此我们一般会对其取对数,把乘积变成加和
,我们把这个乘积称作似然函数 (Likelihood Function)。通常单个点的概率都非常小,很多非常小的数字相乘起来在计算机里非常easy造成浮点数下溢,因此我们一般会对其取对数,把乘积变成加和 ![]() ,得到 log-likelihood function 。接下来我们仅仅要将这个函数最大化(通常的做法是求导并令导数等于零,然后解方程),亦即找到这样一组參数值,它让似然函数取得最大值,我们就觉得这是最合适的參数,这样就完毕了參数预计的过程。
,得到 log-likelihood function 。接下来我们仅仅要将这个函数最大化(通常的做法是求导并令导数等于零,然后解方程),亦即找到这样一组參数值,它让似然函数取得最大值,我们就觉得这是最合适的參数,这样就完毕了參数预计的过程。
以下让我们来看一看 GMM 的 log-likelihood function :
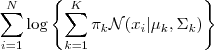
因为在对数函数里面又有加和,我们没法直接用求导解方程的办法直接求得最大值。为了解决问题,我们採取之前从 GMM 中随机选点的办法:分成两步,实际上也就相似于K-means 的两步。
3. 算法流程:
1. 预计数据由每一个 Component 生成的概率(并非每一个 Component 被选中的概率):对于每一个数据  来说,它由第
来说,它由第  个 Component 生成的概率为
个 Component 生成的概率为
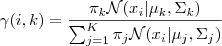
当中N(xi | μk,Σk)就是后验概率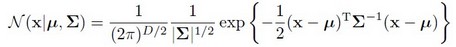 。
。
2. 通过极大似然预计能够通过求到令參数=0得到參数pMiu,pSigma的值。具体请见这篇文章第三部分。
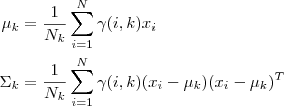
当中  ,而且
,而且  也顺理成章地能够预计为
也顺理成章地能够预计为  。
。
3. 反复迭代前面两步,直到似然函数的值收敛为止。
4. matlab实现GMM聚类代码与解释:
说明:fea为训练样本数据,gnd为样本标号。算法中的思想和上面写的一模一样,在最后的推断accuracy方面,因为聚类和分类不同,仅仅是得到一些 cluster ,而并不知道这些 cluster 应该被打上什么标签,或者说。因为我们的目的是衡量聚类算法的 performance ,因此直接假定这一步能实现最优的相应关系,将每一个 cluster 相应到一类上去。一种办法是枚举全部可能的情况并选出最优解,另外,对于这种问题,我们还能够用 Hungarian algorithm 来求解。具体的Hungarian代码我放在了资源里,调用方法已经写在以下函数中了。
注意:资源里我放的是Kmeans的代码,大家下载的时候仅仅要用bestMap.m等几个文件就好~
1. gmm.m,最核心的函数,进行模型与參数确定。
function varargout = gmm(X, K_or_centroids)
% ============================================================
% Expectation-Maximization iteration implementation of
% Gaussian Mixture Model.
%
% PX = GMM(X, K_OR_CENTROIDS)
% [PX MODEL] = GMM(X, K_OR_CENTROIDS)
%
% - X: N-by-D data matrix.
% - K_OR_CENTROIDS: either K indicating the number of
% components or a K-by-D matrix indicating the
% choosing of the initial K centroids.
%
% - PX: N-by-K matrix indicating the probability of each
% component generating each point.
% - MODEL: a structure containing the parameters for a GMM:
% MODEL.Miu: a K-by-D matrix.
% MODEL.Sigma: a D-by-D-by-K matrix.
% MODEL.Pi: a 1-by-K vector.
% ============================================================
% @SourceCode Author: Pluskid (http://blog.pluskid.org)
% @Appended by : Sophia_qing (http://blog.csdn.net/abcjennifer)
%% Generate Initial Centroids
threshold = 1e-15;
[N, D] = size(X);
if isscalar(K_or_centroids) %if K_or_centroid is a 1*1 number
K = K_or_centroids;
Rn_index = randperm(N); %random index N samples
centroids = X(Rn_index(1:K), :); %generate K random centroid
else % K_or_centroid is a initial K centroid
K = size(K_or_centroids, 1);
centroids = K_or_centroids;
end
%% initial values
[pMiu pPi pSigma] = init_params();
Lprev = -inf; %上一次聚类的误差
%% EM Algorithm
while true
%% Estimation Step
Px = calc_prob();
% new value for pGamma(N*k), pGamma(i,k) = Xi由第k个Gaussian生成的概率
% 或者说xi中有pGamma(i,k)是由第k个Gaussian生成的
pGamma = Px .* repmat(pPi, N, 1); %分子 = pi(k) * N(xi | pMiu(k), pSigma(k))
pGamma = pGamma ./ repmat(sum(pGamma, 2), 1, K); %分母 = pi(j) * N(xi | pMiu(j), pSigma(j))对全部j求和
%% Maximization Step - through Maximize likelihood Estimation
Nk = sum(pGamma, 1); %Nk(1*k) = 第k个高斯生成每一个样本的概率的和,全部Nk的总和为N。
% update pMiu
pMiu = diag(1./Nk) * pGamma' * X; %update pMiu through MLE(通过令导数 = 0得到)
pPi = Nk/N;
% update k个 pSigma
for kk = 1:K
Xshift = X-repmat(pMiu(kk, :), N, 1);
pSigma(:, :, kk) = (Xshift' * ...
(diag(pGamma(:, kk)) * Xshift)) / Nk(kk);
end
% check for convergence
L = sum(log(Px*pPi'));
if L-Lprev < threshold
break;
end
Lprev = L;
end
if nargout == 1
varargout = {Px};
else
model = [];
model.Miu = pMiu;
model.Sigma = pSigma;
model.Pi = pPi;
varargout = {Px, model};
end
%% Function Definition
function [pMiu pPi pSigma] = init_params()
pMiu = centroids; %k*D, 即k类的中心点
pPi = zeros(1, K); %k类GMM所占权重(influence factor)
pSigma = zeros(D, D, K); %k类GMM的协方差矩阵,每一个是D*D的
% 距离矩阵,计算N*K的矩阵(x-pMiu)^2 = x^2+pMiu^2-2*x*Miu
distmat = repmat(sum(X.*X, 2), 1, K) + ... %x^2, N*1的矩阵replicateK列
repmat(sum(pMiu.*pMiu, 2)', N, 1) - ...%pMiu^2,1*K的矩阵replicateN行
2*X*pMiu';
[~, labels] = min(distmat, [], 2);%Return the minimum from each row
for k=1:K
Xk = X(labels == k, :);
pPi(k) = size(Xk, 1)/N;
pSigma(:, :, k) = cov(Xk);
end
end
function Px = calc_prob()
%Gaussian posterior probability
%N(x|pMiu,pSigma) = 1/((2pi)^(D/2))*(1/(abs(sigma))^0.5)*exp(-1/2*(x-pMiu)'pSigma^(-1)*(x-pMiu))
Px = zeros(N, K);
for k = 1:K
Xshift = X-repmat(pMiu(k, :), N, 1); %X-pMiu
inv_pSigma = inv(pSigma(:, :, k));
tmp = sum((Xshift*inv_pSigma) .* Xshift, 2);
coef = (2*pi)^(-D/2) * sqrt(det(inv_pSigma));
Px(:, k) = coef * exp(-0.5*tmp);
end
end
end
2. gmm_accuracy.m调用gmm.m,计算准确率:
function [ Accuracy ] = gmm_accuracy( Data_fea, gnd_label, K )
%Calculate the accuracy Clustered by GMM model
px = gmm(Data_fea,K);
[~, cls_ind] = max(px,[],1); %cls_ind = cluster label
Accuracy = cal_accuracy(cls_ind, gnd_label);
function [acc] = cal_accuracy(gnd,estimate_label)
res = bestMap(gnd,estimate_label);
acc = length(find(gnd == res))/length(gnd);
end
end
3. 主函数调用
gmm_acc = gmm_accuracy(fea,gnd,N_classes);
写了本文进行总结后自己非常受益,也希望大家能够好好YM下上面pluskid的gmm.m,不光是算法,当中的矩阵处理代码也写的非常简洁,非常值得学习。
另外看了两份东西非常受益,一个是pluskid大牛的《漫谈 Clustering (3): Gaussian Mixture Model》,一个是JerryLead的EM算法具体解释,大家有兴趣也能够看一下,写的非常好。
关于Machine Learning很多其它的学习资料与相关讨论将继续更新,敬请关注本博客和新浪微博Sophia_qing。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号