A Floor Tiles

结论

观察AB,发现显然不可能有"P"形状,整个图出和入必然是1对1对的
总共2(n+m)个=>有(n+m)对线段

总线端=完整线+环
没有环很好搞

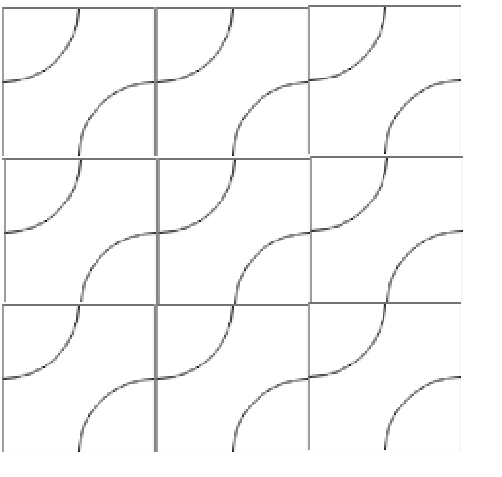
最多环有两种情况

最多 $ \lfloor n/2 \rfloor * \lfloor m/2 \rfloor + \lfloor (n-1)/2 \rfloor * \lfloor (m-1)/2 \rfloor $ 个环

最多 $ \lfloor (n-1)/2 \rfloor * \lfloor m/2 \rfloor + \lfloor n/2 \rfloor * \lfloor (m-1)/2 \rfloor $ 个环

最少都为n+m个曲线

减少环

通过把左右两个砖替换成AA或BB,就能减少1个环





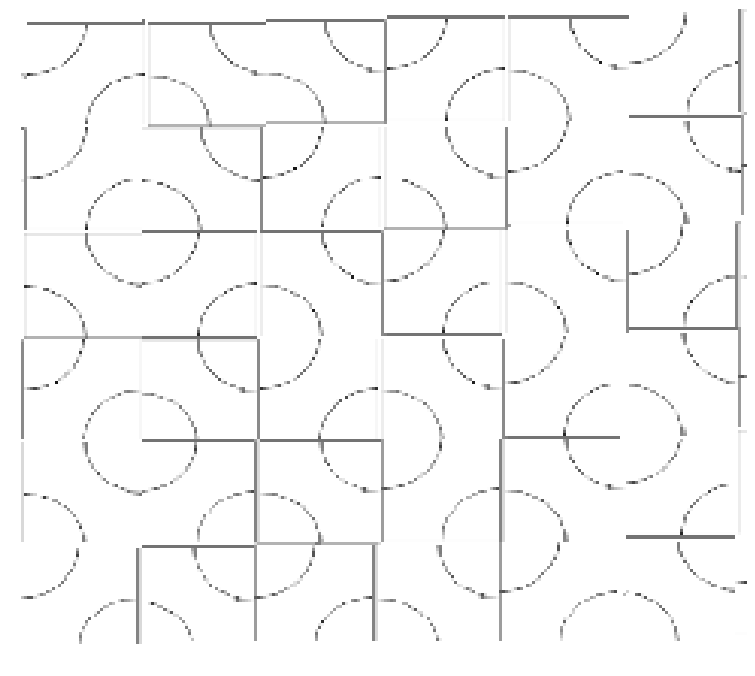
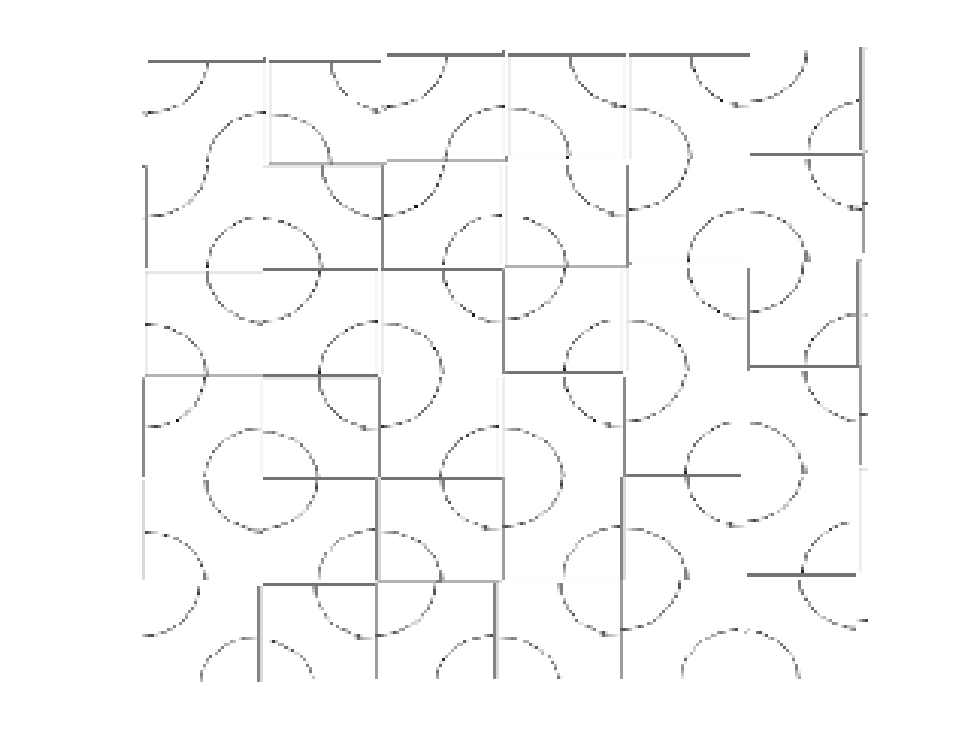
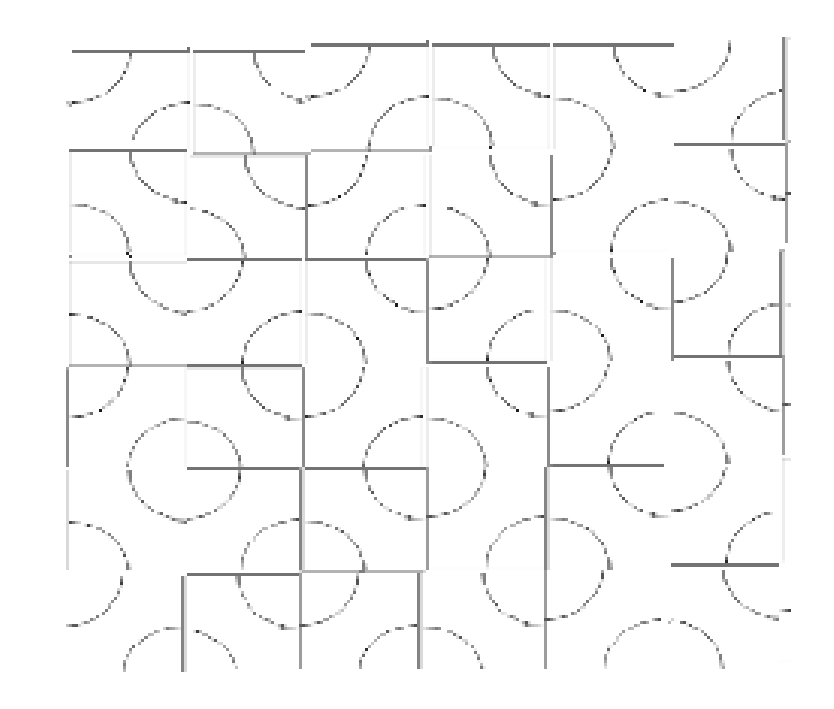
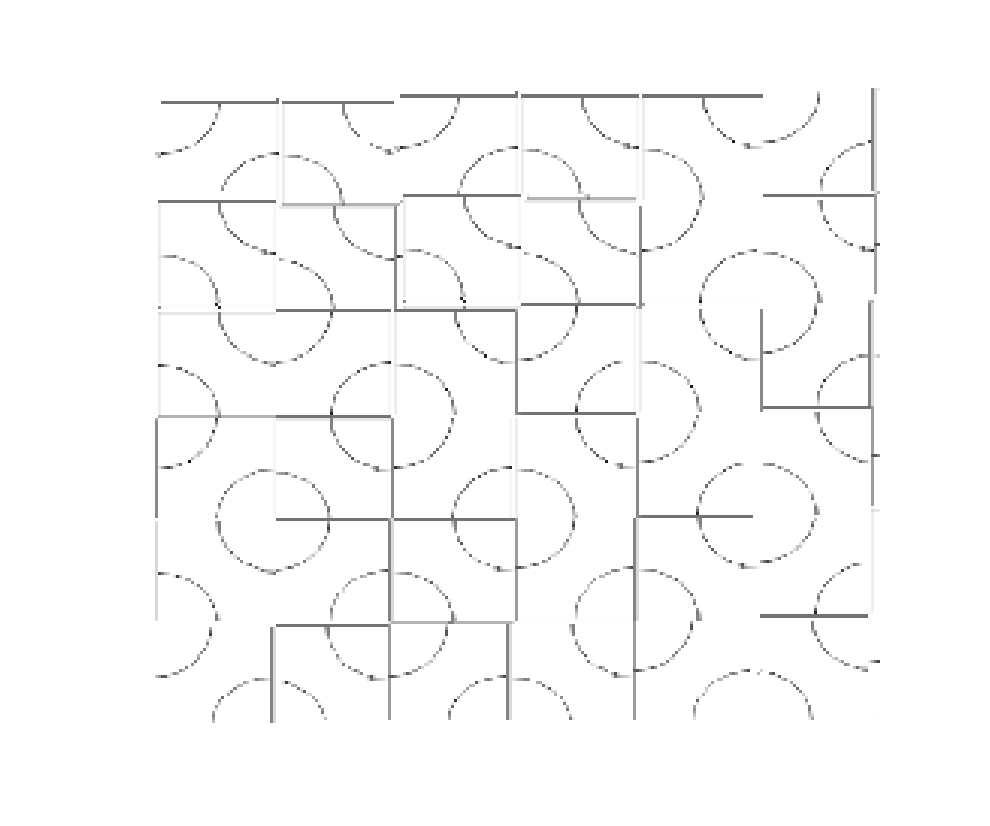
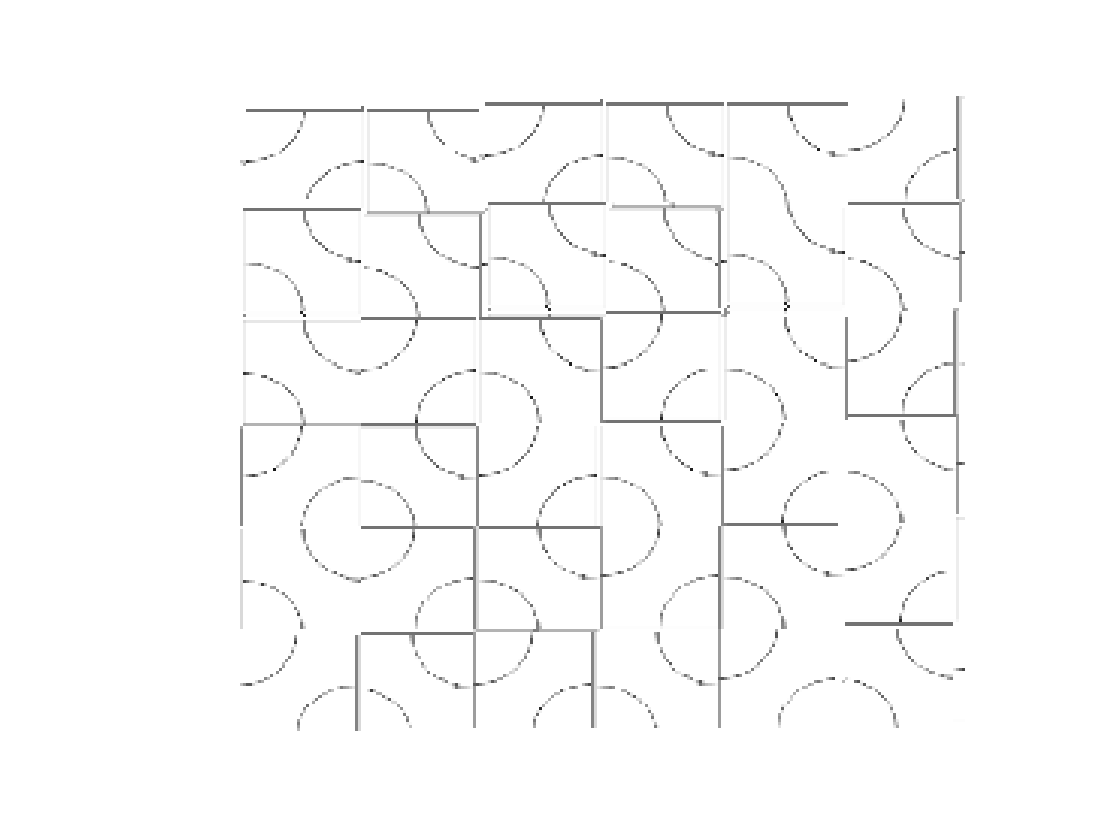
最终会替换成

完全没有环
所以[l,r]都是可行的

构造方法

根据给的一块,先构造出最多的,即AB交替
判断要求是否在答案范围内
然后依次替换就行

启示

遇到构造,尝试最大/好情况和最小/坏情况,看看中间是不是都可行