树上前缀和

树上前缀和

题目链接

多次询问树上的一些路径的权值和

• 点前缀和

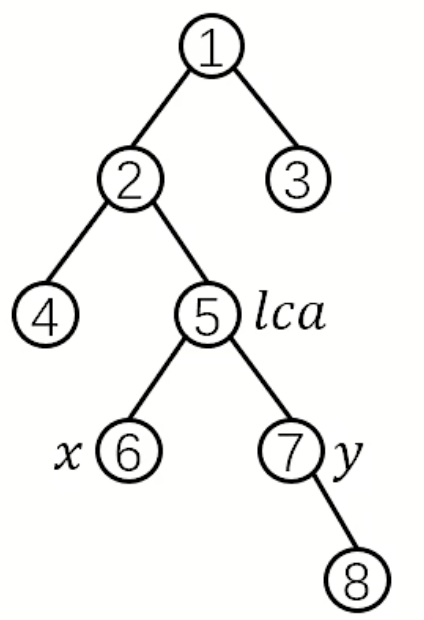
  \(s[i]\)代表从根节点到节点\(i\)的点权和

  先自顶向下计算出前缀和\(s[i]\)，然后利用前缀和拼凑\((x, y)\)的路径和

  \(s[x] + s[y] - s[lca] - s[fa[lca]]\)

  

• 边前缀和

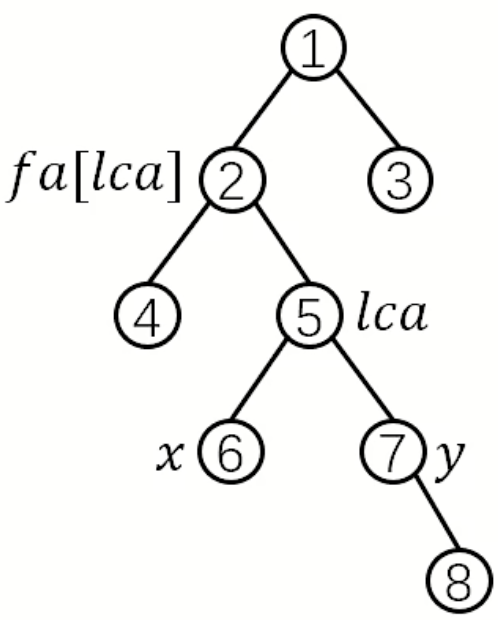
  \(s[i]\)代表从根节点到节点\(i\)的边权和

  先自顶向下计算出前缀和\(s[i]\)，然后利用前缀和拼凑\((x, y)\)的路径和

  \(s[x] + s[y] - 2 * s[lca]\)

  

题解

关键点在于如何求最近公共祖先（LCA）

用倍增法求LCA，LCA详情看LCA篇

#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define ppb pop_back
#define SZ(v) ((int)v.size())
#define pii pair<int, int>
#define int long long
#define all(v) v.begin(), v.end()
#define debug(x) cout << "======" << x << "========" << "\n"
typedef long long ll;
typedef unsigned int u32;
typedef unsigned long long u64;
typedef double db;
using namespace std;
const int N = 1e6+10;
const int mod = 998244353;
int _;

int n, m;
vector<int> e[N];
int dep[N], fa[N][30];
int sum[N][55];
int u, v;

int ksm(int a, int b) {
    a %= mod;
    b %= mod;
    int ans = 1;
    while(b) {
        if(b&1) {
            ans = (ans * a) % mod;
        }
        b >>= 1;
        a = (a * a) % mod;
    }
    return ans;
}

void dfs(int u, int father) {
    dep[u] = dep[father]+1;
    for(int i = 1; i <= 50; i++) {
        sum[u][i] = (ksm(dep[u] - 1, i) + sum[father][i]) % mod;
    }
    fa[u][0] = father;
    for(int i = 1; i <= 19; i++) {
        fa[u][i] = fa[fa[u][i-1]][i-1];
    }
    for(int v : e[u]) {
        if(v == father) continue;
        dfs(v, u);
    }
}

int lca(int u, int v) {
    if(dep[u] < dep[v]) {
        swap(u, v);
    }
    for(int i = 19; i >= 0; i--) {
        if(dep[fa[u][i]] >= dep[v]) {
            u = fa[u][i];
        }
    }
    if(u == v) return u;
    for(int i = 19; i >= 0; i--) {
        if(fa[u][i] != fa[v][i]) {
            u = fa[u][i];
            v = fa[v][i];
        }
    }
    return fa[u][0];
}

void solve() {
    cin >> n;
    for(int i = 1; i <= n - 1; i++) {
        cin >> u >> v;
        e[u].pb(v);
        e[v].pb(u);
    }
    dfs(1, 0);
    int x, y, k;
    cin >> m;
    for(int i = 0; i < m; i++) {
        cin >> x >> y >> k;
        int p = lca(x, y);
        // 注意最后模负数
        cout << ((sum[x][k] + sum[y][k]) % mod - (sum[p][k] + sum[fa[p][0]][k]) % mod + mod) % mod << "\n"; 
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    _ = 1;
    // cin >> _;
    
    while(_--) {
        solve();
    } 
    return 0;
}