算法 | 基础 - [数据结构]
在这里插入代码片@
链表
- 链表分 单向链表 和 双向链表
//单向
Class Node<V>{
V value;
Node next;
}
//双向
Class Node<V>{
V value;
Node next;
Node prev;
}
Hash
- 使用上可以理解为集合结构
- 只有 key ,对应 HashSet
- 有 key 和 value,对应 HashMap
- 有无 value 是上面二者唯一的区别,底层结构一致
- Hash 不会组织 key 的顺序
- 对 Hash 进行 CRUD,时间复杂度 \(O(1)\),但常数较大
- Hash 内部不保存对象
- 基础类型存本身(包括包装类型和
String) - 引用类型存引用(8 byte)
- 基础类型存本身(包括包装类型和
有序表
- 使用上可以理解为集合结构
- 只有 key ,对应 TreeSet
- 有 key 和 value,对应 TreeMap
- 有无 value 是上面二者唯一的区别,底层结构一致
- 有序表会组织 key 的顺序
具体可能由 红黑树、AVL、size--balance-tree、跳表 数实现
因为有序所以具有 Hash 不具备的操作,如:小于等于且最近floorKey()、大于等于且最近deilingKey() - 对有序表进行 CRUD,时间复杂度 \(O(\log{n})\),但常数较大
- 有序表内部不保存对象
- 基础类型存本身(包括包装类型和
String) - 引用类型存引用(8 byte)
- 基础类型存本身(包括包装类型和
- 有序表的元素时引用型时,必须指定比较器
二叉树
示例如下图
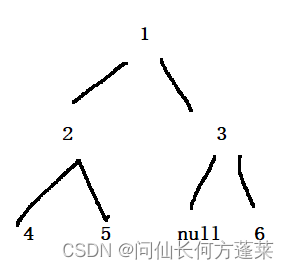
二叉树的子树:是指二叉树中某个节点和它其下所有节点,包括左右孩子的孩子......
搜索二叉树
即所有节点的左树都比右树小
完全二叉树
全满、或最后一层按从左向右顺序渐满大的二叉树
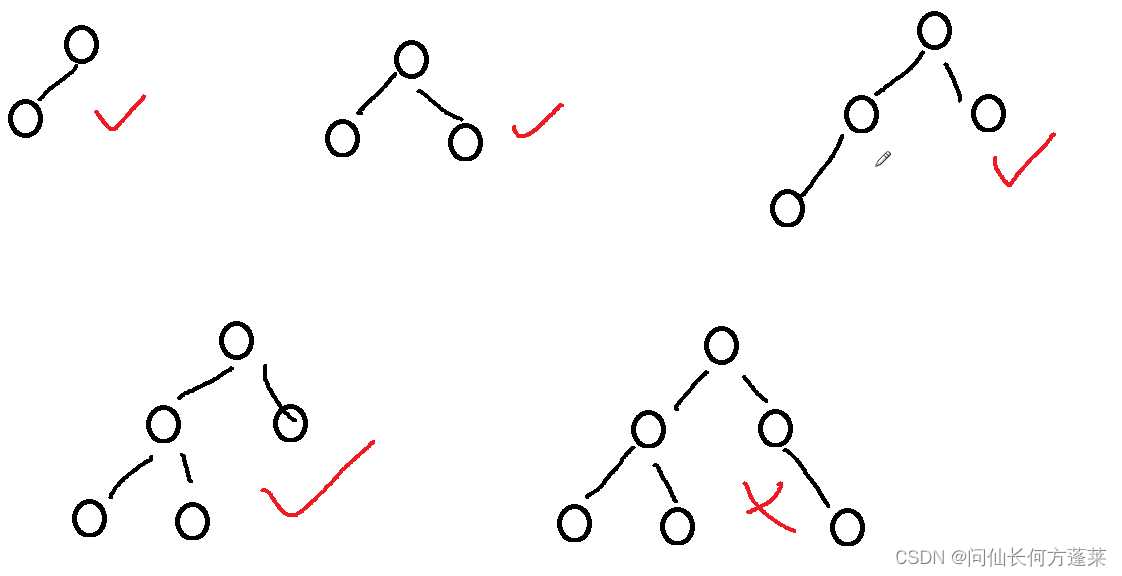
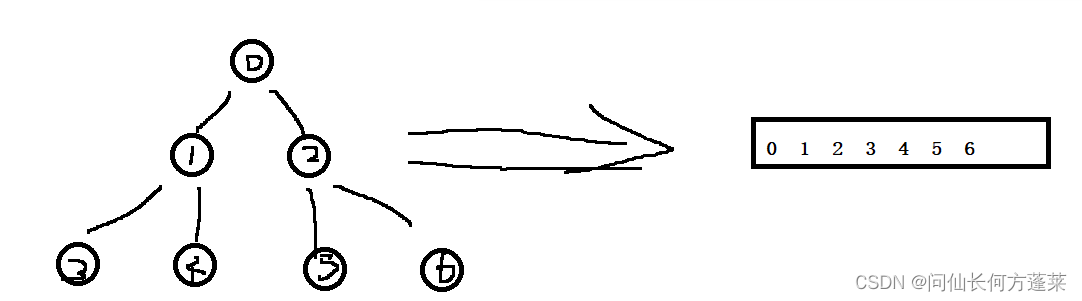
完全二叉树的数组表示
可以把完全二叉树与从 0 开始的数组的对照,如下图,其特性为
- 对某个元素 i 而言,左 child = 2 * i +1
- 对某个元素 i 而言,右 child = 2 * i +2
- 对某个元素 i 而言,父 = (i -1) / 2
平衡二叉树
即所有节点的左树、右树的高度差都 <= 1
因为二叉树的查询和树的深度有直接关系,极端不平衡时,树会退化成链表
堆
堆在数据结构上就是 完全二叉树
堆分为 大顶堆 和 小顶堆
- 大顶堆:若以任意节点的开始,此节点比其下任意节点都大
- 小顶堆:若以任意节点的开始,此节点比其下任意节点都小
堆操作
heap insert (以大顶堆为例)
即,向堆中插入元素
- 数据插入堆
- 计算此元素在堆上的父元素
- 与父元素比较,如果大于父,与父交互
- 如果交换,在与当前父比较并交互,重复至不需要交互
复杂度: \(O(\log{n})\),\(O(1)\)
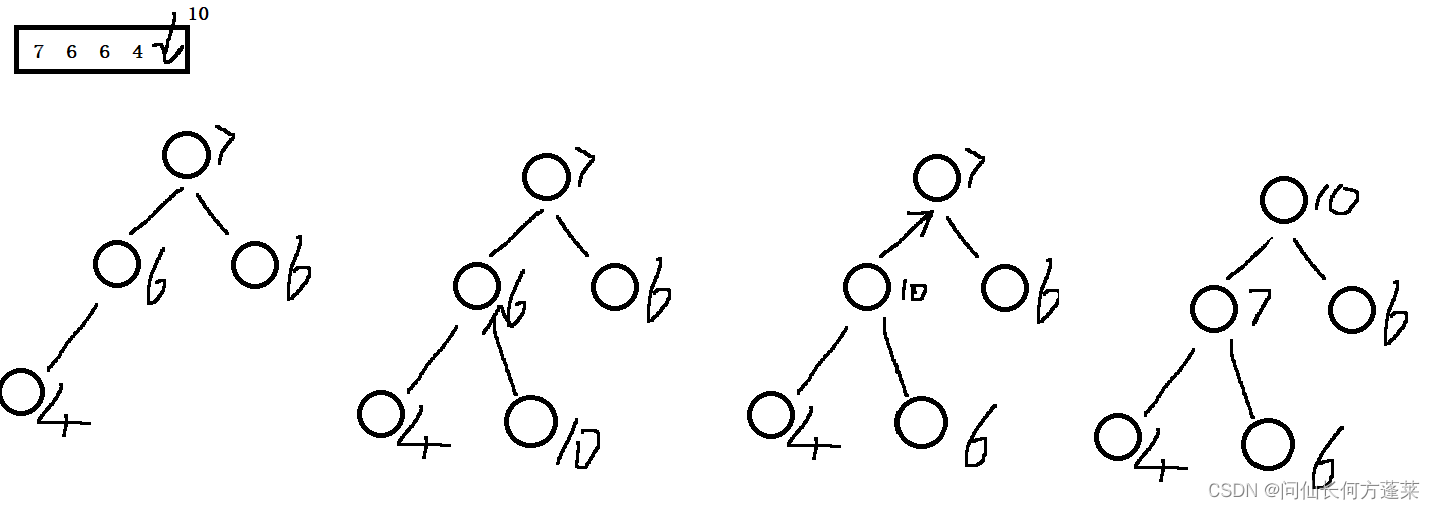
heapify (以大顶堆为例)
删除某个节点后,重构堆
- 将堆最后一个元素复制到被删除元素 e 位置
- heapsize - 1,此时原最后一个位置有值,但已经不属于堆的元素了
- 选出 e 的两个 child 中大的
- 与 e 相比,如果大于 e ,二者交互
- 重复上两步,直到不用交互或超出 heapsize
复杂度: \(O(\log{n})\),\(O(1)\)
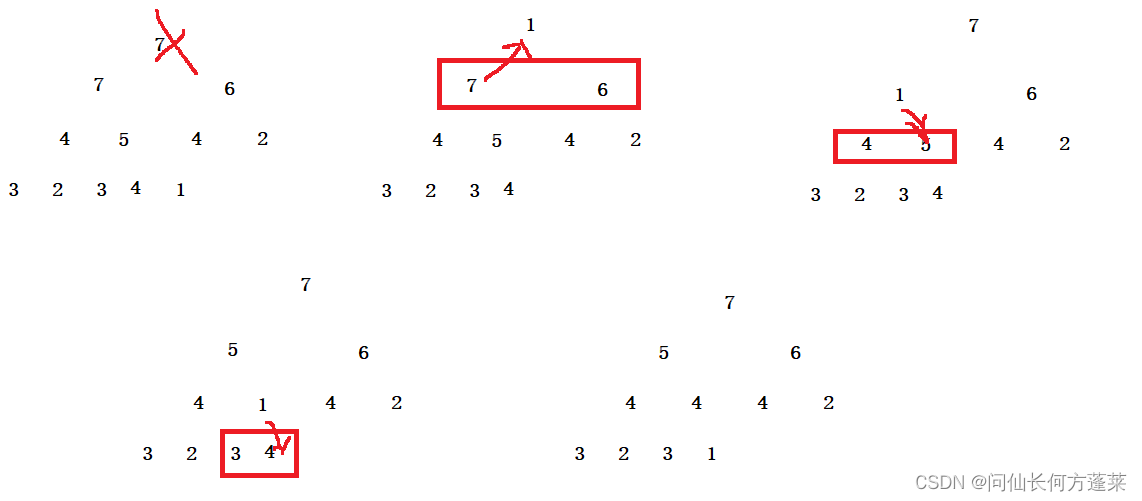
heap 修改
修改堆中某元素的值
- 如果是变大,向上 heap insert
- 如果是变小,向下 heapify
数组整理成堆 (以大顶堆为例)
要求数组完全提供,而不是一个元素一个元素出现
从最后的节点开始,依次进行 heapify
复杂度: \(O(n)\),\(O(1)\)
| 层数 | 节点数 | heapify 步骤数 |
|---|---|---|
| 最大层 | n / 2 | 1 |
| 最大层-1 | n / 4 | 2 |
| 最大层-2 | n/8 | 3 |
| 最大层-3 | n/16 | 4 |
\(T(n) = n/2^1 + n/2^2 * 2 + n/2^3 * 3 + n/2^4 * 4 ...\)
\(2T(n) = n/2^1 * 2 + n/2^1 * 2 + n/2^2 * 3 + n/2^3 * 4 ...\)
错项相减
\(T(n) = n/2^1 + n/2^1 + n/2^2 + n/2^3 ... = n\)
堆扩容
堆实际上是数组的结构,数组可能耗尽,需要扩容
复杂度: \(O( \log{n})\)
添加 n 个元素时,触发 \(\log{n}\) 次扩容,每次复制所有元素,\(O(n)\),即 \(O( n* \log{n})\)
但这是添加 n 个元素时,平均到每个元素 \(O( \log{n})\)
优先级队列(PriorityQueue)
默认相当于一个小顶堆,堆顶优先级高
可以通过指定 Comparator 自定义排序规则,比如实现大顶堆
桶
即指容器,具体什么容器按需求,算法中统称为桶
对于依赖统计的排序,通常会通过拆解元素不同位上的字母进行处理
这是因为虽然元素的值千变万化,但某一位上的字母只有有限的几个,比如纯数字只有 [0-9]
可以用它的权开辟不同数量的桶进行统计,有效减少占用的空间
可以参考 基数排序
使用桶时,通常 空间复杂度为 \(O(n)\),因为有几个元素,所有的桶里加起来就有几个元素
词频表
常用于拆分单词,并统计某一位上各个字面出现的数量
词频表相当于对 桶 的变形,桶 里装的是 某一位=某值的所有元素,词频表里装的是 一位=某值的元素的个数
通常出现在基于统计的排序中,可以参考 基数排序
使用词频表时,通常 空间复杂度为 \(O(\log{n})\),因为每次只考虑某一位上可能出现的值
示例,比如 [11,14,23,24,36,67],对应
- 个位词频表为 [0,1,0,1,2,0,1,1,0,0]
- 十位词频表为 [0,2,2,1,0,0,1,0,0,0]
词序表
在 词频表 的基础上,使 t[i] = t[i] + t[i-1] 即可得到词序表
词序表表示,某一位 <= 某值的元素 的个数,即:某一位 = 某值的元素 时,应该将它放到第几个位置上
通常出现在基于统计的排序中,可以参考 基数排序
使用词序表时,通常 空间复杂度为 \(O(\log{n})\),因为每次只考虑某一位上可能出现的值
示例,若词频表 a 为 [0,1,0,1,2,0,1,1,0,0] ,词序表 b 为 [0,1,1,2,4,4,5,6,6,6]
假设上面的词序表是个位的,以 b[4] = 4 为例,说明原数组中个位 <= 4 的元素有 4 个
则,如果遇到一个个位是 4 的元素,就可以将它放到 == 第 4 个位置== 上
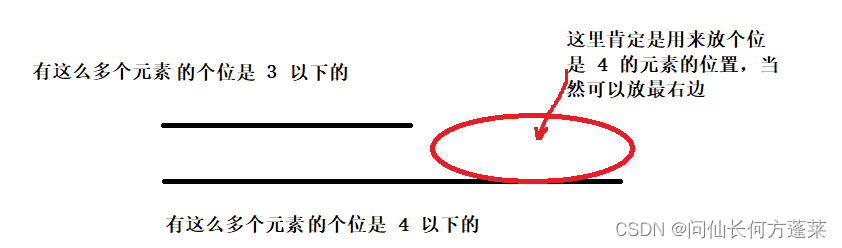
那么就将它放到 == 第 4 个位置== 上,即索引是 [3] 的位置,然后 b[4] - -
这是因为 4 区的这个位置被占用了,下一个个位是 4 的数虽然还得放到上图的区域,但位置就需要往左放一格
图
图是每个节点 可能具有多个前驱节点、也可能具有多个后继节点 的数据结构
图常用于描述具有 多对多 关系的节点集合
常用概念
组成
- 顶点(vertex),即节点
- 边(edge),即两个顶点之间的连线
- 路径
即从一个顶点出发去另一个节点途径顶点和边的顺序
顶点的入度 & 出度
无向图中,任意节点的入度与出度相等
- 入度:有几个顶点指向此顶点
- 出度:顶点指向几个顶点
图的分类
- 无向图
顶点之间的边没有规定方向 - 有向图
顶点之间的边规定了方向 - 带权图
也叫 网,边具有权值的图
图的表示
以下图为例

邻接表法
- 从顶点的角度进行表达
- 依次表达 每个顶点与它的直接邻居
直接邻居:某顶点通过一条边连接到的另一个顶点 - 可以表达带权图,如 a:b(1),c(4)
a:b,c
b:a,e
c:a,d,e
d:c
e:b,c
邻接表法
- 从边的角度进行表达
- 建立图中所有节点的矩阵
- 统计点与点之间有无边、或距离
统计权重时,无边按 ∞ 统计 - 适合表达有向图、带权图
| a | b | c | d | e | |
|---|---|---|---|---|---|
| a | 0 | 1 | 1 | 0 | 0 |
| b | 1 | 0 | 0 | 0 | 1 |
| c | 1 | 0 | 0 | 1 | 1 |
| d | 0 | 0 | 1 | 0 | 0 |
| e | 0 | 1 | 1 | 0 | 0 |
二维数组法
- 从边的角度进行表达
- 相当于一个
int[][3]的二维数组 - 每个小数组形如
[3,4,5]:有一条边,长3,连接4、5 两个顶点
图的通用代码描述
// 整张图
class Graph{
HashMap<Integer,Node> nodes;
HashSet<Edge> edges;
}
// 顶点
class Node{
int value;
int in; // 入度
int out; // 出度
ArrayList<Node> nexts; // 直接邻居,只计算发散出去的点
ArrayList<Edge> edges; // 直接发散出去的边
}
// 边,下面表示为有向边
// 无向边需要下面 2 个 Edge 共同表示
class Edge{
int weight; // 权值
Node from;
Node to;
}
最小生成树
带权图 也被称作 网
包含网中所有节点,且权值和最小的树就是 最小生成树



 浙公网安备 33010602011771号
浙公网安备 33010602011771号