算法 | 基础 - [通用]

@

目录

• 固定规则 & 概念
  • 位与( & )
  • 位异或( ^ )
• 固定公式
  • master 公式
• 固定写法
  • 获取最右位 1
  • 两数平均值
• 常用工具 & 技巧

固定规则 & 概念

位与( & )

a & a = a
0 & a = 0

位异或( ^ )

a ^ a = 0 因此严禁同内存地址 ^ 自己
0 ^ a = a
a ^ b = b ^ a
a ^ b ^ c = a ^ ( b ^ c )
^ 相当于 无进位相加

固定公式

master 公式

• \(T(n) = a * (n / b) + O(n^d)\)
  • a ：等量子问题的个数
  • b：等量子问题有多少个
  • \(O(n^d)\) ： 非子问题之外的结构的复杂度
• 用于估算递归算法的 时间复杂度
  • \(\log{_b}{^a}\) < d，复杂度： \(O(n^d)\)
  • \(\log{_b}{^a}\) == d，复杂度： \(O(n^d * \log{n})\)
  • \(\log{_b}{^a}\) > d，复杂度： \(O(n^{\log{_b}{^a}})\)
• 适用条件：从母问题 上拆出来的 子问题 是等量的
  举例 (n * 1/3) + (n * 2/3) + O(n^d) 不满足 master 公式
  举例 T(n) = 2 * (n / 2) + O(1) 满足 master 公式
  举例 T(n) = 2 * (n * 3/4) + O(1)满足 master 公式（问题分两份，左3/4，右也是 3/4，中间重合了一半，但是无所谓）

固定写法

获取最右位 1

a & (~a + 1)

最右侧 1，说明此位之后都是 0，此位之前无所谓
取反，使所有位在最后的 & 时，都是 0 & 1 = 0，同时最后为 0111....
+ 1 ，使数字的从最后一位开始收到影响，影响结果为使最低位到最右侧 1 位回复原状
&，所有高位都是 0 & 1 = 0，最低位到最右侧 1 位 自己 & 自己 = 自己
于是变成 000...自己，如下面示例

表达式	值
a	xxxxxxxx10000
~a	xxxxxxxx01111
~a + 1	xxxxxxxx10000	此 x 是 a 的 x 的取反
a & (~a + 1)	xxxxxxxx10000

两数平均值

L + (( R - L ) >> 1)
( L + R ) / 2 一般也行，但若二者和超出最大值，则 可能得到一个负数
(( R - L ) >> 1) 必须被括号包裹

常用工具 & 技巧

快慢指针
同时给定两个指针，一个快一个慢，慢指针一次移动一格，快指针一次移动两格

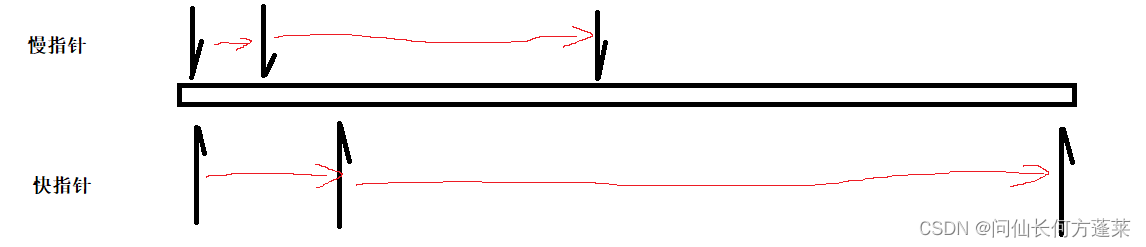
常用于求单项链表的中点

对数器
对数是指：核对数据，而不是 log
若有算法实现 a，不知道对错
则实现很 low 但逻辑上比较万无一失的实现 b
实现一个产生随机数据的工具，即 对数器
n 次运行两种算法实现 a、b，比较其结果
若出现了不一致的结果，则两种算法至少其中之一错了
若 n 次都一致，扩大随机数据的范围
直到认为算法可信

比较器
比较器相当于重载运算符
可以应用于特殊标准的排序
可以应用于特殊标准的排序的结构
即 Comparator 接口，实现 compare(a,b) 方法

• 返回负数，a < b，a 在 b 前
• 返回 0 ，a == b
• 返回正数，a > b ，b 在 a 前