OpenCV基础入门系列基本操作——叁
系列博文第三篇,关于OpenCV4的一些基本操作和使用。
博文主要以实例展示不同的函数使用方法。
OpenCV基础入门系列基本操作——壹
OpenCV基础入门系列基本操作——贰
运行环境,win10 + VS2019 + OpenCV430
本文用到的头文件
#include <iostream>
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
#include <string>
#include <cmath>
using namespace cv;
using namespace std;
1、仿射变换
1)实现旋转及缩放
void test11(const string& path)
//实现旋转及缩放
{
Mat src = imread(path), dst;
cout << src.cols << " " << src.rows << endl;
float angle = 40, scale = 1;
//opencv中 angle < 0,则为顺时针旋转,若 angle > 0,则为顺时针旋转
//scale为缩放倍数,对应缩放大小
Point2f center(src.cols * 0.5, src.rows * 0.5);
Mat affine_matrix = getRotationMatrix2D(center, angle, scale);
warpAffine(src, dst, affine_matrix, src.size());
imshow("旋转前", src);
imshow("旋转后", dst);
waitKey(0);
return;
}
运行结果如下所示:
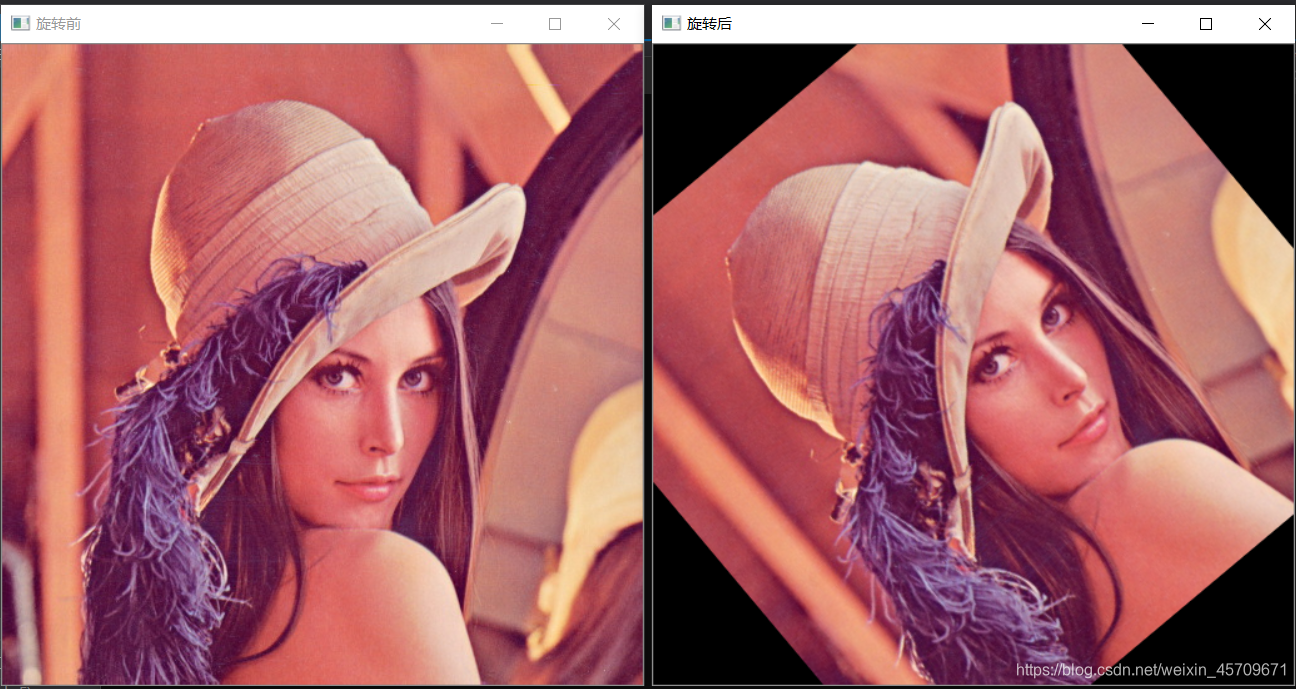
2)实现任意三点的变换
给出三个点,利用OpenCV带有的API
C++ cv::Mat cv::getAffineTransform(const cv::Point2f *src, const cv::Point2f *dst)
获取仿射矩阵,实现仿射操作。
C++ void cv::warpAffine( cv::InputArray src, cv::OutputArray dst, cv::InputArray M, cv::Size dsize, int flags = 1, int borderMode = 0, const cv::Scalar &borderValue = cv::Scalar() )
void test12(const string& path)
//实现任意三点的变换,需要3个点确定一个空间,自由度为6
{
Mat src = imread(path), dst;
//变换前的3点
Point2f src_pt[] = {
Point2f(200,200),
Point2f(250,200),
Point2f(200,100) };
//变换后的3点
Point2f dst_pt[] = {
Point2f(300,100),
Point2f(300,50),
Point2f(200,100) };
Mat affine_matrix = getAffineTransform(src_pt, dst_pt);
warpAffine(src, dst, affine_matrix, src.size());
imshow("三点变换前", src);
imshow("三点变换后", dst);
waitKey(0);
return;
}
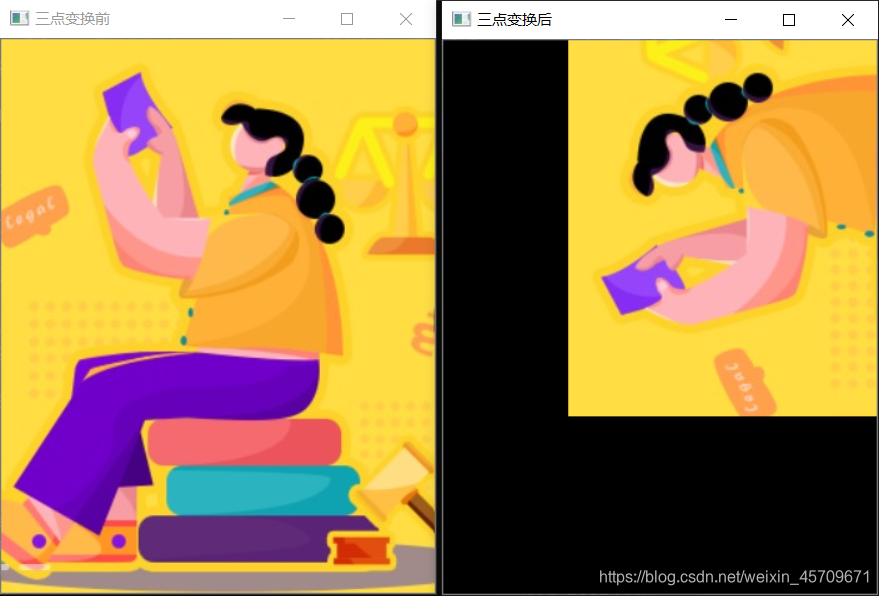
3)实现投影变换
投影变换需要有四个点,计算透视变换的矩阵
void test13(const string& path)
//实现投影变换,需要4个点确定一个空间,自由度为8
{
Mat src = imread(path), dst;
//投影变换前后,在下面两个Point2f数组中,需要每个点位置都一一对应,否则会达不到预期的图片效果
Point2f pts1[] = {
Point2f(0,0),
Point2f(233,0),
Point2f(0,275),
Point2f(233,275) };
Point2f pts2[] = {
Point2f(0,92),
Point2f(233,0),
Point2f(0,184),
Point2f(233,275) };
//根据四个对应点,获取变换矩阵
Mat perspective_matrix = getPerspectiveTransform(pts1, pts2);
//根据变换矩阵,绘制投影的图片
warpPerspective(src, dst, perspective_matrix, src.size());
//展示图片
imshow("投影变换前:", src);
imshow("投影变换后:", dst);
waitKey(0);
return;
}
利用微软的图标做演示:

4)现有如下图像,实现自动矫正成尺寸相同的左图。

void test144(const string& path) {
Mat gray = imread(path, 0), binary;
threshold(gray, binary, 253, 255, THRESH_BINARY_INV);
// 形态学操作
Mat ele = getStructuringElement(MORPH_RECT, Size(3, 3));
morphologyEx(binary, binary, MORPH_ERODE, ele);
imshow("binary", binary);
Mat labels = Mat::zeros(gray.size(), CV_32S), stats, centroids;
//利用连通块标记函数找出中间的图像位置
int num_labels = connectedComponentsWithStats(binary, labels, stats, centroids, 8, 4);
int area = stats.at<int>(1, CC_STAT_AREA);
//cout << "AREA:" << area << endl;
//cout << "总连通块数量:" << (num_labels - 1) << endl << endl;
double side = sqrt(area);
double scale = gray.rows / side;
cout << " gray.rows:" << gray.rows << endl;
cout << "Scale: " << scale << endl;
//利用勾股定理以及三角学解三角形,求得对应旋转的角度,以便还原之前的图像
double theta = (asin(gray.rows / 1.414 / side) - CV_PI / 4) * 180 / CV_PI;
cout << "Theta: " << theta << endl;
//执行旋转操作
Mat src = imread(path), dst;
//opencv中 angle < 0,则为顺时针旋转,若 angle > 0,则为顺时针旋转
//scale为缩放倍数,对应缩放大小
Point2f center(src.cols * 0.5, src.rows * 0.5);
Mat affine_matrix = getRotationMatrix2D(center, theta, scale);
warpAffine(src, dst, affine_matrix, src.size());
imshow("旋转前", src);
imshow("旋转后", dst);
waitKey(0);
return;
}
矫正后效果如下
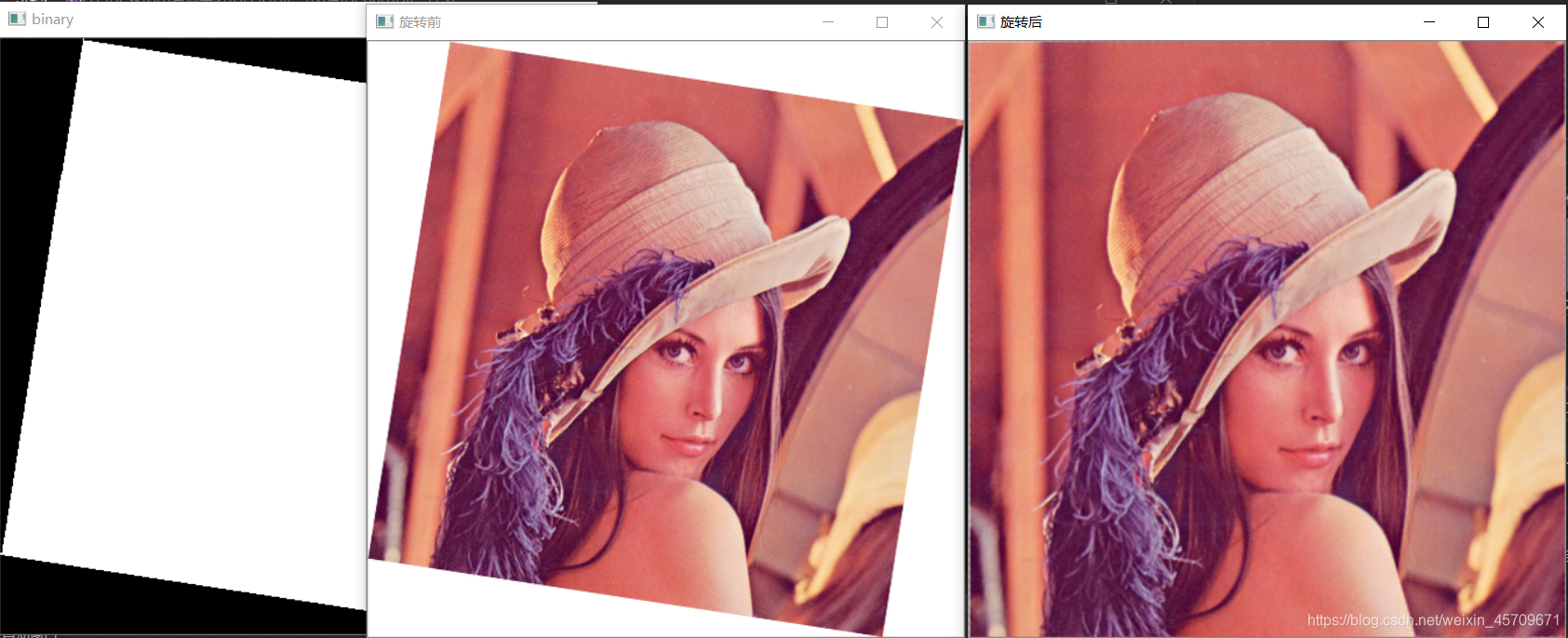
5)通过OpenCV进行图像的旋转后,超出原尺寸的部分,会被自动裁剪,通过对应比例,实现不裁剪的图像旋转(即上例的反向操作)
void test151(const string& path)
//通过OpenCV进行图像的旋转后,超出原尺寸的部分,会被自动裁剪,实现不自动裁剪的图像旋转
{
Mat src = imread(path), dst;
cout << src.cols << " " << src.rows << endl;
float angle = -15.0;
//利用三角函数学,求出对应的缩放比例
float scale = 1 / (sin(fabs(angle) / 180 * 3.1416) + cos(fabs(angle) / 180 * 3.1416));
cout << scale << endl;
//opencv中 angle < 0,则为顺时针旋转,若 angle > 0,则为顺时针旋转
//scale为缩放倍数,对应缩放大小
Point2f center(src.cols * 0.5, src.rows * 0.5);
Mat affine_matrix = getRotationMatrix2D(center, angle, scale);
warpAffine(src, dst, affine_matrix, src.size());
imshow("旋转前", src);
imshow("旋转后", dst);
waitKey(0);
return;
}
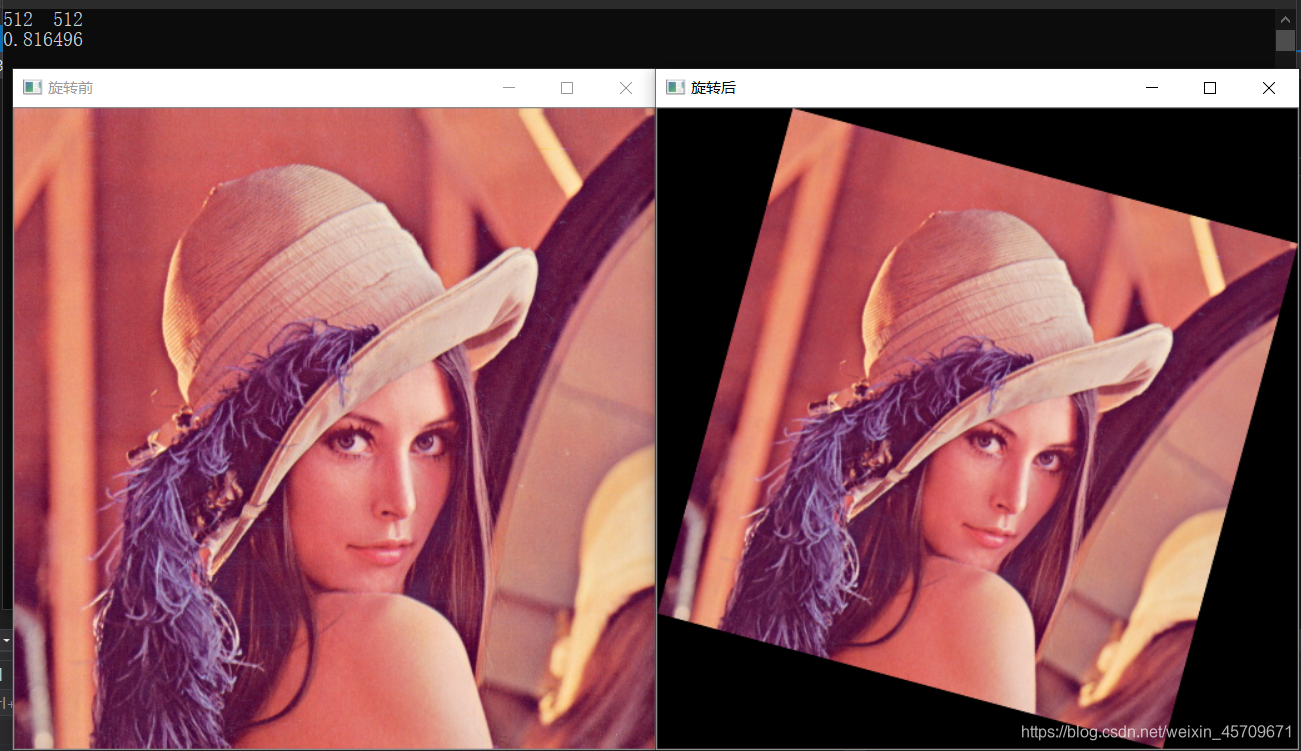
2、霍夫变换
1)调用HoughLines()函数,检测下图的零部件

以下解释参考自网络,侵删。
HoughLines( ),此函数可以找出采用标准霍夫变换的二值图像线条。在OpenCV中,我们可以用其来调用标准霍夫变换SHT和多尺度霍夫变换MSHT的OpenCV内建算法。
- 第一个参数,InputArray类型的image,输入图像,即源图像,需为8位的单通道二进制图像,可以将任意的源图载入进来后由函数修改成此格式后,再填在这里。
- 第二个参数,InputArray类型的lines,经过调用HoughLines函数后储存了霍夫线变换检测到线条的输出矢量。每一条线由具有两个元素的矢量表示,其中,是离坐标原点((0,0)(也就是图像的左上角)的距离。 是弧度线条旋转角度(0垂直线,π/2水平线)。
- 第三个参数,double类型的rho,以像素为单位的距离精度。另一种形容方式是直线搜索时的进步尺寸的单位半径。PS:Latex中/rho就表示 。
- 第四个参数,double类型的theta,以弧度为单位的角度精度。另一种形容方式是直线搜索时的进步尺寸的单位角度。
- 第五个参数,int类型的threshold,累加平面的阈值参数,即识别某部分为图中的一条直线时它在累加平面中必须达到的值。大于阈值threshold的线段才可以被检测通过并返回到结果中。
- 第六个参数,double类型的srn,有默认值0。对于多尺度的霍夫变换,这是第三个参数进步尺寸rho的除数距离。粗略的累加器进步尺寸直接是第三个参数rho,而精确的累加器进步尺寸为rho/srn。
- 第七个参数,double类型的stn,有默认值0,对于多尺度霍夫变换,srn表示第四个参数进步尺寸的单位角度theta的除数距离。且如果srn和stn同时为0,就表示使用经典的霍夫变换。否则,这两个参数应该都为正数。
- 第八个参数,double类型的 min_theta,对于标准和多尺度Hough变换,检查线条的最小角度。必须介于0和max_theta之间。
- 第九个参数,double类型的 max_theta, 对于标准和多尺度Hough变换,检查线条的最大角度。必须介于min_theta和CV_PI之间.
C++: void HoughLines(InputArray image, OutputArray lines, double rho, double theta, int threshold, double srn=0, double stn=0, double min_theta = 0, double max_theta = CV_PI )
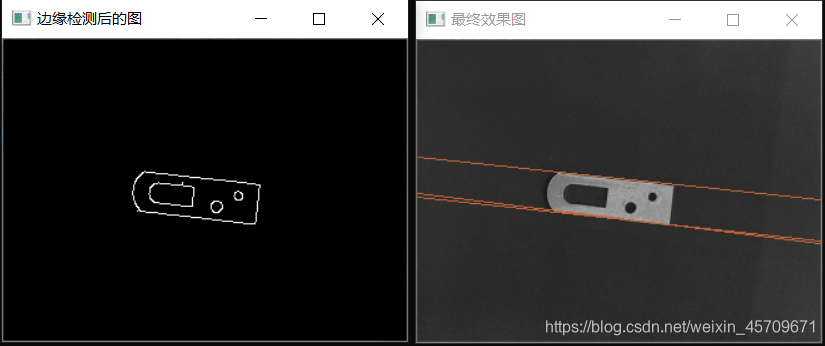
思路:先利用canny算子检测出零件的边缘信息,随后利用霍夫变换找直线,绘制出相应的直线
代码:
void test211(const string& path)
{
//实现霍夫变换
Mat image = imread(path);
Mat midImage;
Canny(image, midImage, 50, 200, 3);
vector<Vec2f> lines;
HoughLines(midImage, lines, 1, CV_PI / 180, 56); // 输入的时二值图像,输出vector向量
for (size_t i = 0; i < lines.size(); i++) {
float rho = lines[i][0]; //就是圆的半径r
float theta = lines[i][1]; //就是直线的角度
Point pt1, pt2;
double a = cos(theta), b = sin(theta);
double x0 = a * rho, y0 = b * rho;
pt1.x = cvRound(x0 + 1000 * (-b));
pt1.y = cvRound(y0 + 1000 * (a));
pt2.x = cvRound(x0 - 1000 * (-b));
pt2.y = cvRound(y0 - 1000 * (a));
line(image, pt1, pt2, Scalar(55, 100, 195), 1);
}
imshow("边缘检测后的图", midImage);
imshow("最终效果图", image);
waitKey(0);
}
2)调用HoughLinesP()
HoughLinesP(),此函数在HoughLines的基础上末尾加了一个代表Probabilistic(概率)的P,表明它可以采用累计概率霍夫变换(PPHT)来找出二值图像中的直线。
C++: void HoughLinesP(InputArray image, OutputArray lines, double rho, double theta, int threshold, double minLineLength=0, double maxLineGap=0 )
- 第一个参数,InputArray类型的image,输入图像,即源图像,需为8位的单通道二进制图像,可以将任意的源图载入进来后由函数修改成此格式后,再填在这里。
- 第二个参数,InputArray类型的lines,经过调用HoughLinesP函数后后存储了检测到的线条的输出矢量,每一条线由具有四个元素的矢量(x_1,y_1, x_2, y_2) 表示,其中,(x_1, y_1)和(x_2, y_2) 是是每个检测到的线段的结束点。
- 第三个参数,double类型的rho,以像素为单位的距离精度。另一种形容方式是直线搜索时的进步尺寸的单位半径。
- 第四个参数,double类型的theta,以弧度为单位的角度精度。另一种形容方式是直线搜索时的进步尺寸的单位角度。
- 第五个参数,int类型的threshold,累加平面的阈值参数,即识别某部分为图中的一条直线时它在累加平面中必须达到的值。大于阈值threshold的线段才可以被检测通过并返回到结果中。
- 第六个参数,double类型的minLineLength,有默认值0,表示最低线段的长度,比这个设定参数短的线段就不能被显现出来。
- 第七个参数,double类型的maxLineGap,有默认值0,允许将同一行点与点之间连接起来的最大的距离。
void test222(const string& path)
{
//1. 读取图像
Mat src, canny, dst;
src = imread(path);
imshow("src", src);
//2. 获取边缘
Canny(src, canny, 100, 200);
imshow("canny", canny);
//3. 转成灰度图像
cvtColor(canny, dst, COLOR_GRAY2BGR);//将二值图转换为RGB图颜色空间,这里重新创建一张空Mat也行
//4. 霍夫变换检测
vector<Vec4f> plines;//保存霍夫变换检测到的直线
HoughLinesP(canny, plines, 1, CV_PI / 180, 10, 15, 8);//提取边缘时,会造成有些点不连续,所以maxLineGap设大点
/*
第一个参数,InputArray类型的image,输入图像,即源图像,需为8位的单通道二进制图像,可以将任意的源图载入进来后由函数修改成此格式后,再填在这里。
第二个参数,InputArray类型的lines,经过调用HoughLinesP函数后后存储了检测到的线条的输出矢量,每一条线由具有四个元素的矢量(x_1,y_1, x_2, y_2表示,
其中,(x_1, y_1)和(x_2, y_2) 是是每个检测到的线段的结束点。
第三个参数,double类型的rho, 以像素为单位的距离精度。 另一种形容方式是直线搜索时的进步尺寸的单位半径。
第四个参数,double类型的theta,以弧度为单位的角度精度。另一种形容方式是直线搜索时的进步尺寸的单位角度。
第五个参数,int类型的threshold,累加平面的阈值参数,即识别某部分为图中的一条直线时它在累加平面中必须达到的值。
大于阈值 threshold 的线段才可以被检测通过并返回到结果中。
第六个参数,double类型的minLineLength,有默认值0,表示最低线段的长度,比这个设定参数短的线段就不能被显现出来。
第七个参数,double类型的maxLineGap,有默认值0,允许将同一行点与点之间连接起来的最大的距离。
*/
//5. 显示检测到的直线
Scalar color = Scalar(0, 0, 255);//设置颜色
for (size_t i = 0; i < plines.size(); i++)
{
Vec4f hline = plines[i];
line(dst, Point(hline[0], hline[1]), Point(hline[2], hline[3]), color, 2, LINE_AA);//绘制直线
}
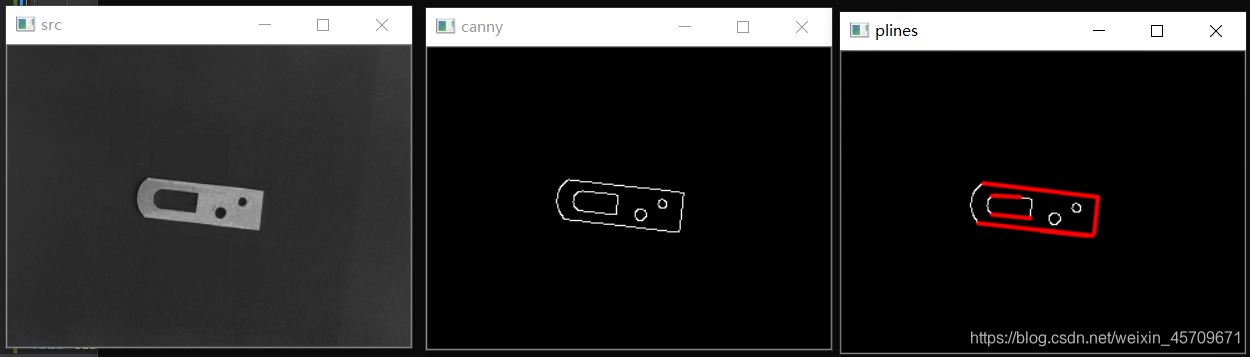
imshow("plines", dst);
waitKey(0);
}
3.算法与策略
1)算法
图像降噪,直方图增强,二值化,频率分析,图像形态学,几何信息提取,特征提取,等各种数学方法。尽可能多的输出结果。
2)策略
筛选出实际需要的结果。需要的信息和干扰信息的本质差距。
1)检测下图机械部件的结构

方法一及对应代码实现:
先读入图片进行二值化处理,再利用连通域标记,找到可能的区域,最后利用面积筛选出需要的零件信息
void test311(const string& path)
{
Mat image = imread(path);
// 二值化
Mat gray, binary;
cvtColor(image, gray, COLOR_BGR2GRAY);
threshold(gray, binary, 0, 255, THRESH_BINARY_INV | THRESH_OTSU);
// 形态学操作
Mat ele = getStructuringElement(MORPH_RECT, Size(3, 3));
morphologyEx(binary, binary, 3, ele);
namedWindow("binary", WINDOW_NORMAL);
imshow("binary", binary);
Mat labels = Mat::zeros(image.size(), CV_32S);
Mat stats, centroids;
int num_labels = connectedComponentsWithStats(binary, labels, stats, centroids, 8, 4);
vector<Vec3b> colors(num_labels);
//背景颜色
colors[0] = Vec3b(0, 0, 0);
int b, g, r;
for (int i = 1; i < num_labels; i++) {
b = sin(i + 1) * cos(i + 1) * 255;
g = cos(i + 2) * 255;
r = sin(i + 3) * 255;
colors[i] = Vec3b(b, g, r);
}
// 标记结果
Mat dst = Mat::zeros(image.size(), image.type());
int w = image.cols;
int h = image.rows;
for (int row = 0; row < h; row++) {
for (int col = 0; col < w; col++) {
int label = labels.at<int>(row, col);
if (label == 0) continue;
dst.at<Vec3b>(row, col) = colors[label];
}
}
for (int i = 1; i < num_labels; i++) {
Vec2d pt = centroids.at<Vec2d>(i, 0);
int x = stats.at<int>(i, CC_STAT_LEFT);
int y = stats.at<int>(i, CC_STAT_TOP);
int width = stats.at<int>(i, CC_STAT_WIDTH);
int height = stats.at<int>(i, CC_STAT_HEIGHT);
int area = stats.at<int>(i, CC_STAT_AREA);
if (area > 1000 && area < 8000){
//利用面积筛选零部件
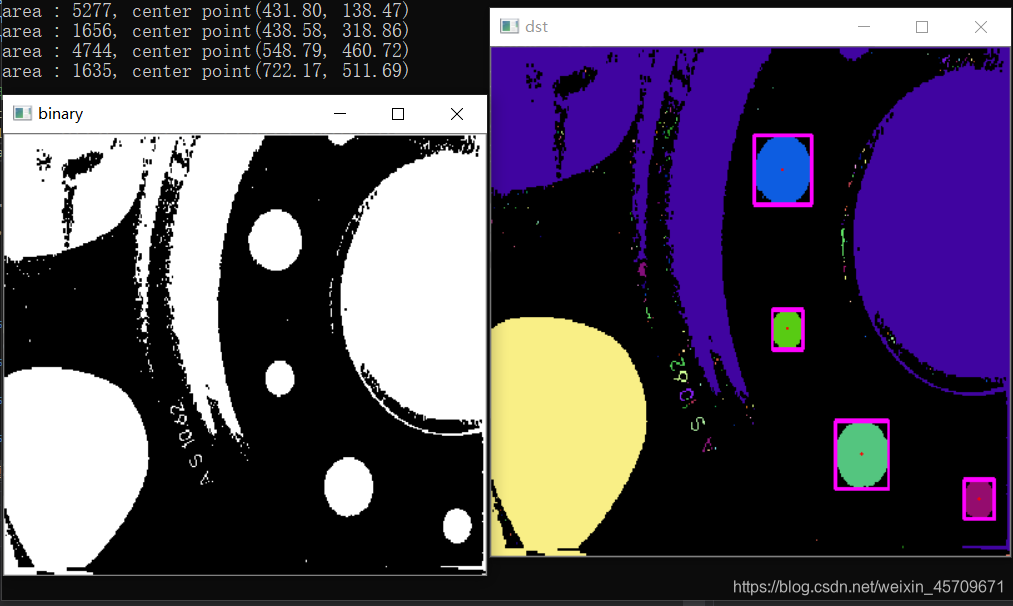
printf("area : %d, center point(%.2f, %.2f)\n", area, pt[0], pt[1]);
circle(dst, Point(pt[0], pt[1]), 2, Scalar(0, 0, 255), -1, 8, 0); //画出连通域的质心
rectangle(dst, Rect(x, y, width, height), Scalar(255, 0, 255), 3, 8, 0);
}
}
namedWindow("dst", WINDOW_NORMAL);
imshow("dst", dst);
waitKey(0);
return;
}
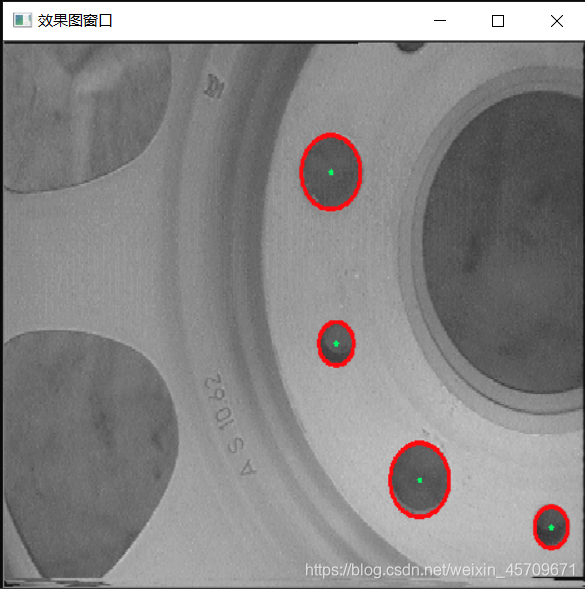
方法二级对应代码实现:
利用霍夫圆来检测微小零部件
void test312(const string& path)
{
//利用霍夫圆检测图中的圆
Mat src = imread(path), src1, dst;
cvtColor(src, src1, COLOR_BGR2GRAY);//转化边缘检测后的图为灰度图
vector<Vec3f> circles;
HoughCircles(src1, circles, HOUGH_GRADIENT, 1.6, 10, 200, 50, 10, 50);
/*
第一个参数,InputArray类型的image,输入图像,即源图像,需为8位的灰度单通道图像。
第二个参数,InputArray类型的circles,经过调用HoughCircles函数后此参数存储了检测到的圆的输出矢量,每个矢量由包含了3个元素的浮点矢量(x, y, radius)表示。
第三个参数,int类型的method,即使用的检测方法,目前OpenCV中就霍夫梯度法一种可以使用,它的标识符为 HOUGH_GRADIENT,在此参数处填这个标识符即可。
第四个参数,double类型的dp,用来检测圆心的累加器图像的分辨率于输入图像之比的倒数,且此参数允许创建一个比输入图像分辨率低的累加器。上述文字不好理解的话,来看例子吧。
例如,如果dp= 1时,累加器和输入图像具有相同的分辨率。如果dp=2,累加器便有输入图像一半那么大的宽度和高度。
第五个参数,double类型的minDist,为霍夫变换检测到的圆的圆心之间的最小距离,即让我们的算法能明显区分的两个不同圆之间的最小距离。
这个参数如果太小的话,多个相邻的圆可能被错误地检测成了一个重合的圆。反之,这个参数设置太大的话,某些圆就不能被检测出来了。
第六个参数,double类型的param1,有默认值100。它是第三个参数method设置的检测方法的对应的参数。对当前唯一的方法霍夫梯度法CV_HOUGH_GRADIENT,
它表示传递给canny边缘检测算子的高阈值,而低阈值为高阈值的一半。
第七个参数,double类型的param2,也有默认值100。它是第三个参数method设置的检测方法的对应的参数。对当前唯一的方法霍夫梯度法CV_HOUGH_GRADIENT,
它表示在检测阶段圆心的累加器阈值。它越小的话,就可以检测到更多根本不存在的圆,而它越大的话,能通过检测的圆就更加接近完美的圆形了。
第八个参数,int类型的minRadius,有默认值0,表示圆半径的最小值。
第九个参数,int类型的maxRadius,也有默认值0,表示圆半径的最大值。需要注意的是,使用此函数可以很容易地检测出圆的圆心,但是它可能找不到合适的圆半径
*/
for (size_t i = 0; i < circles.size(); i++)
{
Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
int radius = cvRound(circles[i][2]);
circle(src, center, 3, Scalar(100, 255, 0), -1, 8, 0);
circle(src, center, radius, Scalar(15, 10, 255), 3, 8, 0);
}
namedWindow("效果图窗口", WINDOW_NORMAL);//定义窗口
imshow("效果图窗口", src);
waitKey(0);
return;
}
运行结果如下:
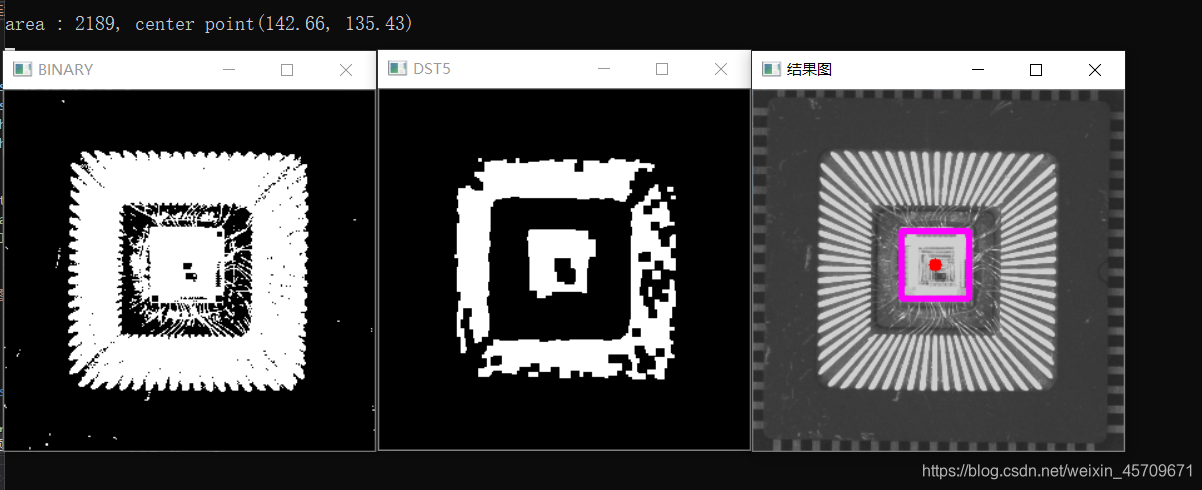
2)标记处下图中芯片的位置

图像形态学的一系列操作,诸如腐蚀,膨胀等等,结构元素若为3x3的正方形,那么最后得到的结果也比较 方正 ,或者说接近于正方形。因此可以用在本例中筛选出芯片的位置。
实现代码如下:
void test322(const string& path)
{
Mat src = imread(path), binary, dst;
cvtColor(src, binary, COLOR_BGR2GRAY);
threshold(binary, binary, 100, 255, THRESH_BINARY);
imshow("BINARY", binary);
Mat ele = getStructuringElement(MORPH_RECT, Size(3, 3));
//利用形态学的一系列操作,逐步使得中间的芯片区域被分离出来
morphologyEx(binary, dst, MORPH_ERODE, ele);
imshow("DST1", dst);
morphologyEx(dst, dst, MORPH_ERODE, ele);
imshow("DST2", dst);
morphologyEx(dst, dst, MORPH_ERODE, ele);
imshow("DST3", dst);
morphologyEx(dst, dst, MORPH_OPEN, ele);
imshow("DST4", dst);
morphologyEx(dst, dst, MORPH_OPEN, ele);
imshow("DST5", dst);
//利用连通域函数,设置范围,利用面积大小筛选芯片所在的区域
Mat labels = Mat::zeros(src.size(), CV_32S);
Mat stats, centroids;
int num_labels = connectedComponentsWithStats(dst, labels, stats, centroids, 8, 4);
cout << "总连通块数量:" << (num_labels - 1) << endl << endl;
for (int i = 1; i < num_labels; i++) {
Vec2d pt = centroids.at<Vec2d>(i, 0);
int x = stats.at<int>(i, CC_STAT_LEFT);
int y = stats.at<int>(i, CC_STAT_TOP);
int width = stats.at<int>(i, CC_STAT_WIDTH);
int height = stats.at<int>(i, CC_STAT_HEIGHT);
int area = stats.at<int>(i, CC_STAT_AREA);
if (1500 < area && 3000 > area) {
printf("area : %d, center point(%.2f, %.2f)\n", area, pt[0], pt[1]);
rectangle(src, Rect(x, y, width, height), Scalar(255, 0, 255), 1, 8, 0);
circle(src, Point((x + width / 2), (y + height / 2)), 5, Scalar(0, 0, 255), -1, 8, 0); //画出中心位置
}
}
imshow("结果图", src);
waitKey(0);
return;
}
展示部分图片如下:中间图片为形态学操作后的二值化图像,中间的芯片区域较为明显。
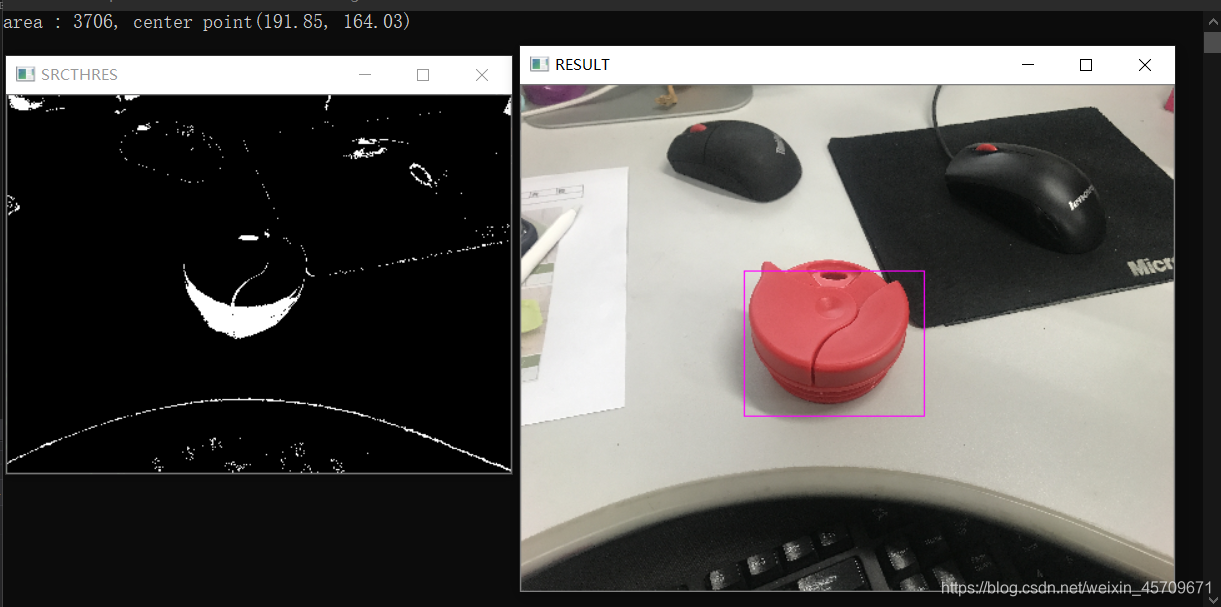
3)标记处图中的红色零部件(下图原图分辨率较高,因此在代码中压缩了处理分辨率的函数,以便更快的得出结果)
本例中,由于原图的分辨率为4032x3024,这种分辨率对于计算机而言,进行复杂操作时,需要大量的计算,本例均在CPU上运行,因此需要在不影响结果的前提下,对读入的图片进行压缩处理,加快处理速度。

先利用HSV颜色空间限制函数,对图像二值化处理,然后利用连通域标记函数处理之
void test333(const string& path)
{
Mat src, srcThreshold, dst;
//对读入的图像进行处理
src = imread(path);
double scale = 0.1;
Size dsize = Size(src.cols * scale, src.rows * scale);
Mat resizedSrc = Mat(dsize, CV_32S);
resize(src, resizedSrc, dsize);
cvtColor(resizedSrc, srcThreshold, COLOR_BGR2HSV);
inRange(resizedSrc, Scalar(14, 4, 75), Scalar(90, 93, 180), srcThreshold);
imshow("SRCTHRES", srcThreshold);
Mat ele = getStructuringElement(MORPH_RECT, Size(3, 3));
//利用形态学的一系列操作,逐步使得中间分离出来
morphologyEx(srcThreshold, dst, MORPH_DILATE, ele);
//imshow("DST1", dst);
morphologyEx(dst, dst, MORPH_DILATE, ele);
//imshow("DST2", dst);
morphologyEx(dst, dst, MORPH_DILATE, ele);
//imshow("DST3", dst);
morphologyEx(dst, dst, MORPH_CLOSE, ele);
//imshow("DST4", dst);
//利用连通域函数,以及对应的面积筛选出目标
Mat labels = Mat::zeros(resizedSrc.size(), CV_32S);
Mat stats, centroids;
int num_labels = connectedComponentsWithStats(dst, labels, stats, centroids, 8, 4);
Mat dst2 = Mat::zeros(resizedSrc.size(), resizedSrc.type());
for (int i = 1; i < num_labels; i++) {
Vec2d pt = centroids.at<Vec2d>(i, 0);
int x = stats.at<int>(i, CC_STAT_LEFT);
int y = stats.at<int>(i, CC_STAT_TOP);
int width = stats.at<int>(i, CC_STAT_WIDTH);
int height = stats.at<int>(i, CC_STAT_HEIGHT);
int area = stats.at<int>(i, CC_STAT_AREA);
if (3600 < area && area < 4000) { //利用面积筛选出合适的区域
printf("area : %d, center point(%.2f, %.2f)\n", area, pt[0], pt[1]);
rectangle(src, Rect(x / scale, y / scale, width / scale, height / scale), Scalar(255, 0, 255), 1/scale, 8, 0);
//还原图像时,需要放大对应的比例
}
}
namedWindow("RESULT", WINDOW_NORMAL);
imshow("RESULT", src);
waitKey(0);
return;
}
结果如下:
后续还会补充有关霍夫变换的数学原理及相应的理解。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号