城市

题目简要

• 有\(n\)个城市，第\(i\)城市有对应属性\(a_i\)和\(c_i\)。

• 现在要从任意城市出发，经过其他城市恰好一次，最后回到起点。

• 从第\(i\)个城市到第\(j\)个城市花费为\(max(c_i,a_j-a_i)\)。

• 求最小花费。

---

转换

• 易得\(max(c_i,a_j-a_i)=c_i+max(0,a_j-(a_i+a_j))\)。

• 因为没个城市都会转移一次，所以可以将贡献拆分。变量\(ans\)为累计贡献的函数，因此先将\(ans\)赋值为\(\sum\limits_{i=1}^nc_i\)。

• 现在，我们可以将第\(i\)个城市比作一座山，山的高度为\(a_i\)，每个山顶都有一个电梯,电梯最高可达高度为\(a_i+c_i\)，相当于电梯可在\(a_i\)至\(a_i+c_i\)内自由活动。

• 费用则相当于从较矮的山向较高的山向上爬行距离（向上爬行指不乘电梯上升距离）。

---

• 从一座山到另一座山，上山可能花钱可能不花钱，下山则一定不花钱。因此，我们只用讨论上山的过程。

• 因题目要求，我们必须经过每一座山。所以我们要到达海拔最矮的山，也要到达海拔最高的山。

• 这样，问题便转换为如何花最少的钱，从海拔最矮的山逐一向上攀爬到海拔最高的山（因为这样能一直上山，后面一直下山）。

---

做法

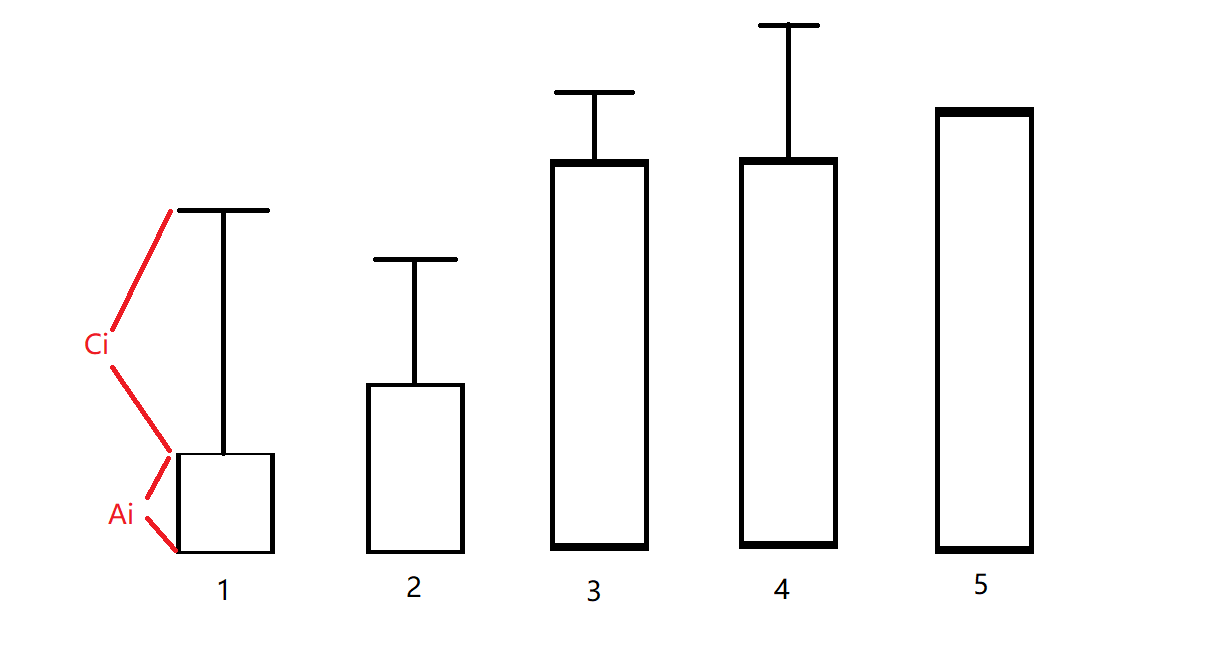
• 我们按山的海拔进行排序（这样才能保证一直上山）。

• 起点在1号山，1号山能不花钱就到达2号山，那我们是否要从1号山到2号山呢？其实是不需要。因为在1号山可到达的范围比2号山大（\(a_1+c_1>a_2+c_2\)）。因为要登山，所以从1号山只好花些钱到达3号山。因为3号山能免费到4号山，并且4号山可到达的范围比3号山大（\(a_4+c_4>a_3+c_3\)），所以我们选择从3号山到4号山，最后从4号山到5号山。

• 我们将上述过程模拟，就行了。

#include<bits/stdc++.h>
using namespace std;
int n,b[100005],ma;
long long ans;
struct kkk
{
  int b,c;
}a[100005];
bool cmp(kkk x,kkk y)
{
  return x.b!=y.b ? x.b<y.b :x.c<y.c;
}
int main()
{
  scanf("%d",&n);
  for(int i=1; i<=n; i++)
  {
  	scanf("%d%d",&a[i].b,&a[i].c);
  	ans+=a[i].c;
  }
  sort(a+1,a+1+n,cmp);
  ma=a[1].b+a[1].c;
  for(int i=1; i<=n; i++)
  {
  	if(a[i].b>ma) ans+=(a[i].b-ma);
  	ma=max(ma,a[i].b+a[i].c);	
  }
  printf("%lld",ans);
  return 0;
}