leetcode 剑指offer 7 重建二叉树

问题描述：输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

解题思路：

前序遍历性质： 节点按照 [ 根节点 | 左子树 | 右子树 ] 排序。
中序遍历性质： 节点按照 [ 左子树 | 根节点 | 右子树 ] 排序。

根据以上性质，可得出以下推论：

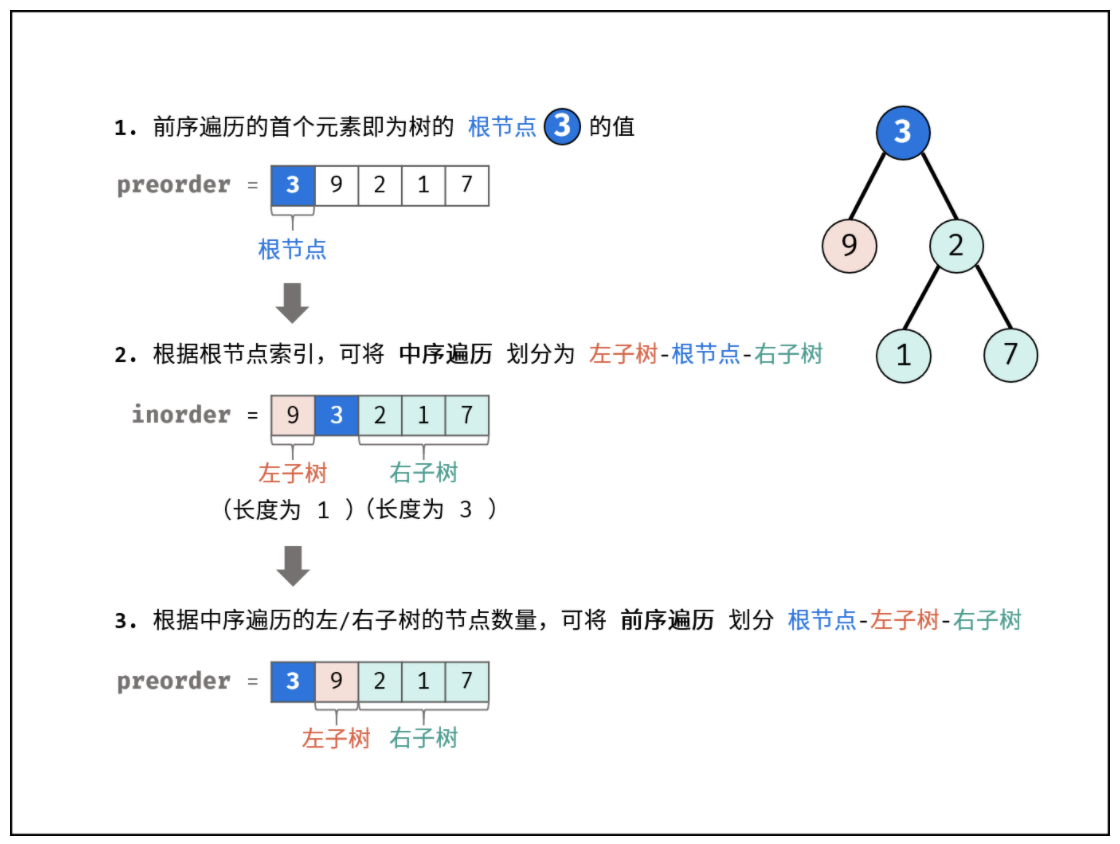
前序遍历的首元素 为 树的根节点 node 的值。
在中序遍历中搜索根节点 node 的索引 ，可将 中序遍历 划分为 [ 左子树 | 根节点 | 右子树 ] 。
根据中序遍历中的左 / 右子树的节点数量，可将 前序遍历 划分为 [ 根节点 | 左子树 | 右子树 ]。

以上子树的递推性质是 分治算法 的体现，考虑通过递归对所有子树进行划分。

分治算法解析：
递推参数： 根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right ；

终止条件： 当 left > right ，代表已经越过叶节点，此时返回 nullptr ；

递推工作：

• 建立根节点 node ： 节点值为 preorder[root] ；

• 划分左右子树： 查找根节点在中序遍历 inorder 中的索引 i ；

  为了提升效率，本文使用哈希表 dic 存储中序遍历的值与索引的映射，查找操作的时间复杂度为 O(1)O(1)

• 构建左右子树： 开启左右子树递归；

  	根节点索引	中序遍历左边界	中序遍历右边界
  左子树	root + 1	left	i - 1
  右子树	i - left + root + 1	i + 1	right

返回值： 回溯返回 node ，作为上一层递归中根节点的左 / 右子节点；

题解：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *      TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        this->preorder = preorder;
        int i = 0;
        for(auto node : inorder)
        {
            this->inorder[node] = i;
            ++i;
        }
        return recur(0, 0, this->preorder.size() - 1);
    }
private:
    vector<int> preorder;
    unordered_map<int, int> inorder; 
    TreeNode* recur(int root, int left, int right)
    {   
        if(left > right) return nullptr;
        TreeNode* node = new TreeNode(preorder[root]);
        int i = inorder[preorder[root]];
        node->left = recur(root + 1, left, i - 1);
        node->right = recur(root + i - left + 1, i + 1, right);
        return node;
    }
};