leetcode 剑指offer 4 二维数组中的查找

问题：在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

解题思路：
若使用暴力法遍历矩阵 matrix ，则时间复杂度为 O(NM)O(NM) 。暴力法未利用矩阵 “从上到下递增、从左到右递增” 的特点，显然不是最优解法。

如下图所示，我们将矩阵逆时针旋转 45° ，并将其转化为图形式，发现其类似于 二叉搜索树 ，即对于每个元素，其左分支元素更小、右分支元素更大。因此，通过从 “根节点” 开始搜索，遇到比 target 大的元素就向左，反之向右，即可找到目标值 target 。

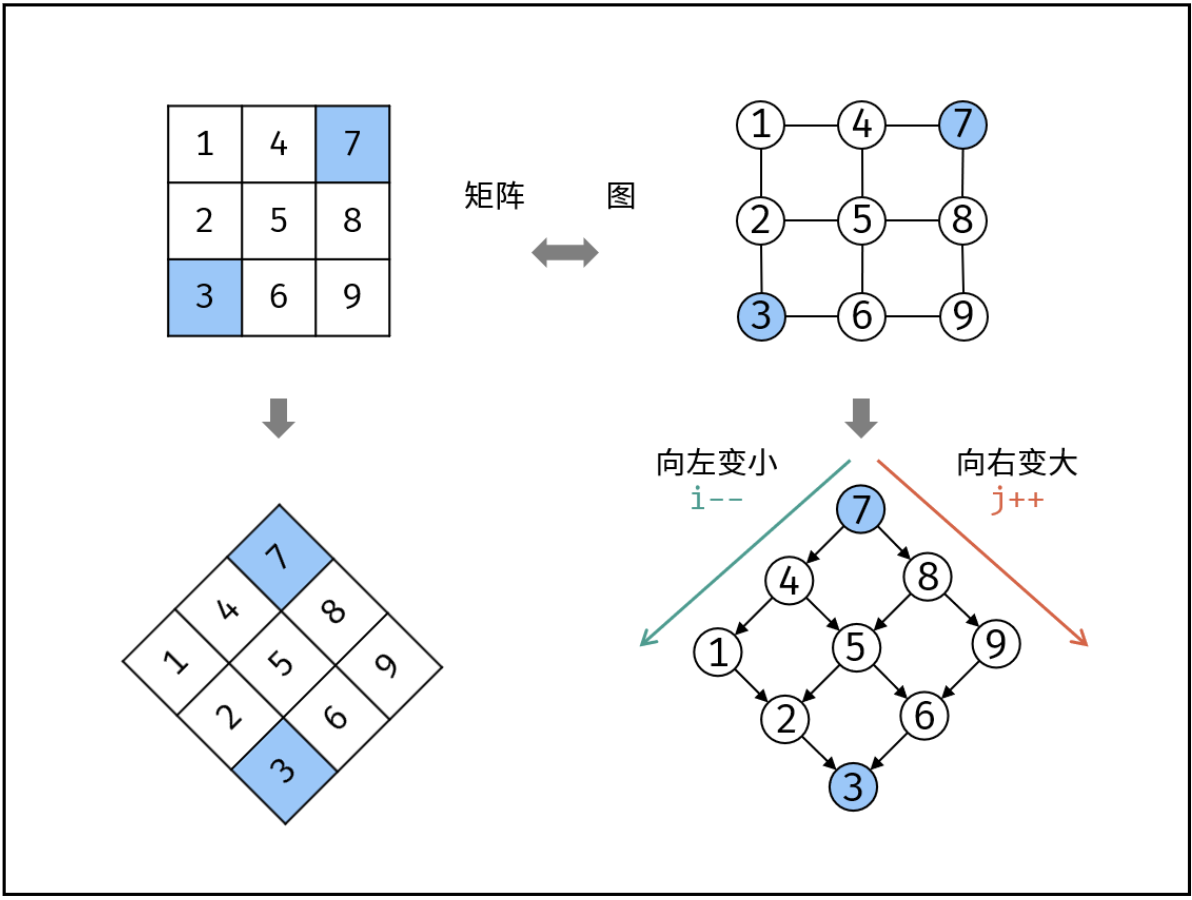
“根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素，本文称之为 标志数 ，以 matrix 中的 左下角元素 为标志数 flag ，则有:

• 若 flag > target ，则 target 一定在 flag 所在 行的上方 ，即 flag 所在行可被消去。
• 若 flag < target ，则 target 一定在 flag 所在 列的右方 ，即 flag 所在列可被消去。

算法流程：

• 从矩阵 matrix 左下角元素（索引设为 (i, j) ）开始遍历，并与目标值对比：
• 当 matrix[i][j] > target 时，执行 i-- ，即消去第 i 行元素；
• 当 matrix[i][j] < target 时，执行 j++ ，即消去第 j 列元素；
• 当 matrix[i][j] = target 时，返回 truetrue ，代表找到目标值。
• 若行索引或列索引越界，则代表矩阵中无目标值，返回 falsefalse 。
• 每轮 i 或 j 移动后，相当于生成了“消去一行（列）的新矩阵”， 索引(i,j) 指向新矩阵的左下角元素（标志数），因此可重复使用以上性质消去行（列）。

复杂度分析：
时间复杂度 O(M+N)O(M+N) ：其中，NN 和 MM 分别为矩阵行数和列数，此算法最多循环 M+NM+N 次。
空间复杂度 O(1)O(1) : i, j 指针使用常数大小额外空间。

class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        int i = matrix.size() - 1, j = 0;
        while(i >= 0 && j < matrix[0].size())
        {
            if(matrix[i][j] > target) --i;
            else if(matrix[i][j] < target) ++j;
            else return true;
        }
        return false;
    }
};