24暑期第七次训练C组
A
生活大爆炸版石头剪刀布
纯模拟,保证AB之间能对应就行。
给出较朴素做法。
bool caiquan(int,int);
int main(void)
{
int n,x,y,ans1 = 0,ans2 = 0,stp;
cin >> n >> x >> y;
vector<int> a(x);
vector<int> b(y);
for(auto &i : a) cin >> i;
for(auto &i : b) cin >> i;
for(int i=0,j=0,t=0;t < n;t++)
{
ans1 += caiquan(a[i],b[j]);
ans2 += caiquan(b[j],a[i]);
++i,++j;
if(i == x) i = 0;
if(j == y) j = 0;
}
cout << ans1 << ' ' << ans2 << '\n';
}
bool caiquan(int a,int b)
{
bool ans = false;
if(a == 0)
{
if(b == 2 || b == 3) ans = true;
}
else if(a == 1)
{
if(b == 0 || b == 3) ans = true;
}
else if(a == 2)
{
if(b == 1 || b == 4) ans = true;
}
else if(a == 3)
{
if(b == 2 || b == 4) ans = true;
}
else
{
if(b == 0 || b == 1) ans = true;
}
return ans;
}
B
笨小猴
模拟,可以开map模拟,但是只出现字符,开数字模拟也可,甚至更快。
void func()
{
string st;
cin >> st;
map<char,int> cnt;
for(auto &i : st) cnt[i]++;
int mx = 0, mn = 0x3f3f;
for(auto &i : cnt)
{
mx = max(mx,i.second);
mn = min(mn,i.second);
}
if(slove(mx - mn)) cout << "Lucky Word\n" << mx - mn << '\n';
else cout << "No Answer\n0";
}
bool slove(int z)// 判素数
{
if(z <= 1) return false;
for(int i=2;i<=z/i;++i)
{
if(z % i == 0) return false;
}
return true;
}
C
过河卒
超纲题,二维dp。
根据题意,卒只能王下或者往右移动,所以 \([i,j]\) 状态由\([i-1,j]\)和\([i,j-1]\)转移。
设\(dp[i][j]\)为移动到\((i,j)\)的次数,那么可得转移方程:
\(dp[i][j] = dp[i-1][j] + dp[i][j-1]\)
但是因为马的存在,有部分点不可移动,这时只需要单独处理,到此处时\(dp[i][j] = 0\)即可。
因为想着最后一组题,特意出了点超纲的考算法的题目。其实可能也不超纲,你们专业课好像学了动态规划。
void func()
{
int n,m,a,b;
cin >> n >> m >> a >> b;
int dp[N][N];
int vis[N][N];
n += 2,m += 2,a += 2,b += 2;// 保证边界往外一格存在,防RE
memset(vis,0,sizeof vis);
memset(dp,0,sizeof dp);
int dx[] = {1,2,2,1,-1,-2,-2,-1};
int dy[] = {2,1,-1,-2,-2,-1,1,2};// 表示马的移动
dp[1][2] = 1;
vis[a][b] = 1;
for(int i=0;i<8;++i) vis[a+dx[i]][b+dy[i]] = 1;// 计算马禁止的坐标
for(int i=2;i<=n;++i)
{
for(int j=2;j<=m;++j)
{
dp[i][j] = dp[i-1][j] + dp[i][j-1];
if(vis[i][j] == 1) dp[i][j] = 0;
}
}
cout << dp[n][m] << '\n';
}
D
Contest Proposal
因为数据很小,可以写暴力一点。
每次比较\(a_i,b_i\),\(a_i\)不符合条件删去,然后把\(b_i\)放入,再给\(a\)排序。这样就能保证顺序了。这时复杂度\(O(n^2logn)\)。
void func()
{
int n,ans = 0;
cin >> n;
vector<int> a(n),b(n);
for(auto &i : a) cin >> i;
for(auto &i : b) cin >> i;
for(int i=0;i<n;++i)
{
if(b[i] < a[i])
{
a.pop_back();
a.push_back(b[i]);
sort(a.begin(),a.end());
ans ++;
}
}
cout << ans << '\n';
}
实际可以用更短的代码写出\(O(n)\)的解法。
因为在\(a_i > b_i\)后插入了新数字,这个数字大小一定在\(a_{i-1}\)和\(a_i\)之间,所以和\(b_{i+1}\)比较的还是\(a_i\)。具体如下。
void func()
{
int n,ans = 0;
cin >> n;
vector<int> a(n),b(n);
for(auto &i : a) cin >> i;
for(auto &i : b) cin >> i;
for(int i=0,j=0;j<n;++j)
{
if(a[i] <= b[j]) ++i;
else ans++;
}
cout << ans << '\n';
}
E
Coin Games
每个人操作实际只有以下三种情况。
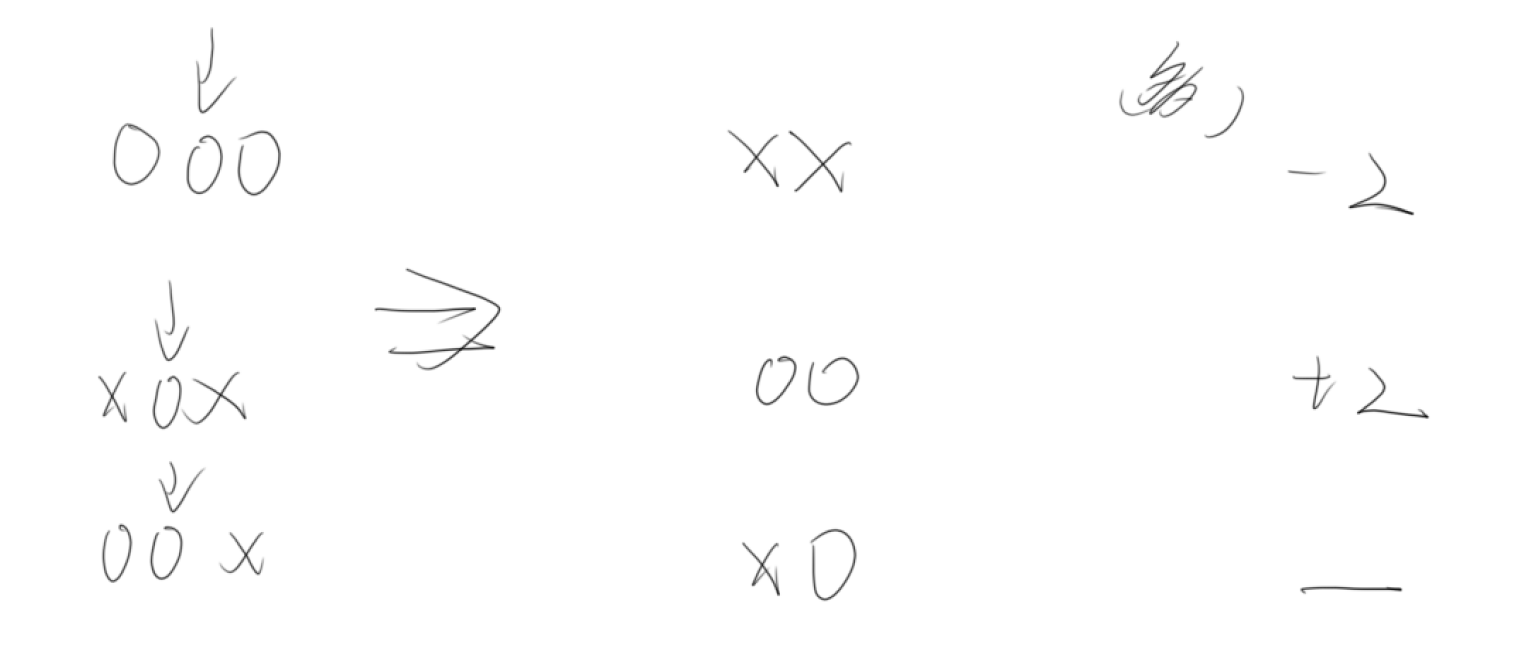
分别使实际可操作次数\(+2,-2,\)不变。在边界操作不翻转,可理解成第三种情况。每次操作都使得可操作次数\(-1\)后偶数次变化,都不影响结果。因为答案就是可操作次数的奇偶性。
void func()
{
int n;
string st;
cin >> n >> st;
int cnt = 0;
for(int i=0;i<n;++i)
if(st[i] == 'U') cnt++;
if(cnt % 2) cout << "YES\n";
else cout << "NO\n";
}
F
Phone Desktop
每个屏幕\(3 \times 5\),可放\(2\)个\(2 \times 2\),其余可填\(7\)个\(1 \times 1\)先算\(2 \times 2\)需要多少个屏幕,再算当前屏幕是否可放下所有\(1 \times 1\),根据\(1 \times 1\)的量加屏幕。
void func()
{
int a,b;
cin >> a >> b;
int ans = (b+1) / 2;
int stp = a - (ans*15 - 4*b);
if(stp > 0) ans += (stp + 14) / 15;
//当前屏幕是否可以放下所有a,不能则再加屏幕.
cout << ans << '\n';
}
G
Chess For Three
因为每次对弈都使总分\(+2\),所以总分不是偶数则不可能。
又因为求最大可能和棋次数。那么先考虑全和棋的情况。
全和棋和棋数为得分\(/2\),因为\(c\)得分最高,所以参与了最多次的对弈。
考虑极限情况,所有对弈都有\(c\)参与。可得:
- 在\(a + b = c\) 时,\(a,b\)可以全向\(c\)和棋。答案即为总分\(/2\)。
进而可推得:
- 在\(a + b < c\) 时,全和棋不满足答案,\(a,b\)全向\(c\)和棋,\(c\)再赢若干次。和棋次最多。答案即\((a+b) / 2\)
- 在\(a + b > c\) 时,全和棋是满足答案的。答案即为总分\(/2\)。
void func()
{
int a,b,c;
cin >> a >> b >> c;
int sum = 0;
sum = a + b + c;
if(sum % 2 == 0) cout << (a + b >= c ? sum / 2 : a + b) << '\n';
else cout << -1 << '\n';
}
H
Symmetric Encoding
按题意处理出\(r\)串,使得对称映射就行。
void func()
{
int n;
string st,r;
cin >> n >> st;
r = st;
sort(r.begin(),r.end());
r.erase(unique(r.begin(),r.end()),r.end());
int len = r.size();
map<char,char> mp;
for(int i=0;i<len;++i) mp[r[i]] = r[len - 1 - i];
for(int i=0;i<n;++i) st[i] = mp[st[i]];
cout << st << '\n';
}
I
Little Nikita
设放上的操作有\(x\)次,拿下的操作有\(y\)次,那么可得
- $x = y = n $
- $x - y = m $
那么\(n + m = 2 \times x\),\(n + m\)为偶数。
void func()
{
int n,m;
cin >> n >> m;
if((n + m) % 2 == 0 && n >= m) cout << "YES\n";
else cout << "NO\n";
}
J
Update Queries
题意说明:可以将\(s\)按\(ind\)数组的索引替换为\(b\)中对应字符。对\(ind\)和\(b\)排序,使得结果字符串的字典序最小。
因为并不需要输出排列后的\(ind\)和\(b\),所以只需要输出最小字典序的答案即可,二者排序并不重要。
只需要将\(ind\)代表的可替换位置,从前到后替换为\(b\)中从小到大的字符。
void func()
{
int n,m;
cin >> n >> m;
string s,c;
cin >> s;
set<int> ind;
while(m--)
{
int stp;cin >> stp;
ind.insert(stp);
}
cin >> c;
sort(c.begin(),c.end());
int j=0;
for(auto &i : ind) s[i-1] = c[j++];
cout << s << '\n';
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号