红黑树总结

二叉查找树

--- 在介绍红黑树前我们需要先了解二叉查找树的概念和特点。

特点

1. 左子树上所有节点的值均小于根节点的值;
2. 右子树上所有节点的值均大于根节点的值;
3. 左右子树也分别为二叉排序树;

优点

查找快捷，二分查找。查找的最大次数为二叉树的高度。

缺陷

二叉查找树在插入节点时，也是一层一层的比较大小后找到合适的插入位置进行插入。所以当连续插入的值已经有序时（如连续插入7,6,5,4,3），按照二叉查找树的特点，这些节点会依次连接在同一边。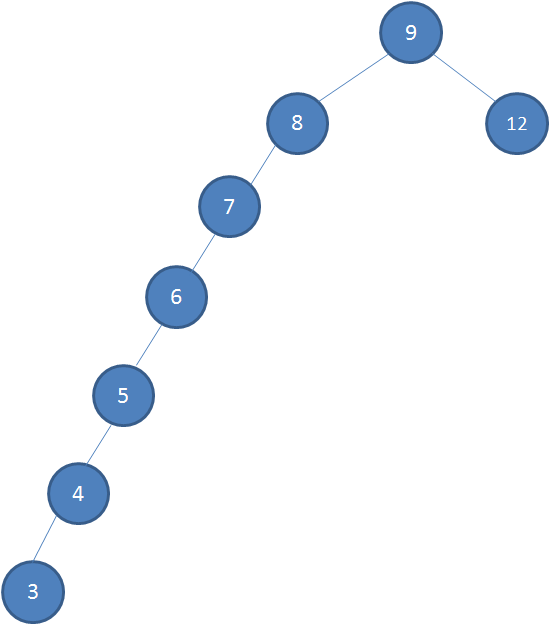
在这种情况下，再来进行查找。就会发现二叉查找树的优势荡然无存。在极端情况下查找时间甚至可能会变成线性的。
为了解决这一问题，后面便提出了红黑树的概念。

红黑树

---

红黑树是一个特殊的二叉查找树，不同之处在于。它是自平衡的，也就是说，在每次进行插入删除操作后红黑树都会自动的进行相应的调整来保证自身相对平衡，不会出现上面提到的效率降低的问题。

性质

下面这些规则的限制，能够保证红黑树的自平衡且算法的复杂度最小（目前来说）。

1. 红黑树的节点分为红色节点和黑色节点两种;
2. 根节点为黑色;
3. 所有叶子节点为黑色;（NIL空节点，用来标识树在此结束--可以降低操作的复杂度）
4. 每个红色节点必须有两个黑色的子节点;（保证了每个叶子到根节点的所有路径上都不能出现连续两个红色节点）
5. 任一节点到其每个叶子的所有简单路径（没有重复节点的路径）都包含相同数目的黑色节点。（此规则和规则4一起限制了红黑树的根节点到叶子的最长路径不会超过最短路径的2倍--最短全黑，最长黑红交替，保证了平衡性）
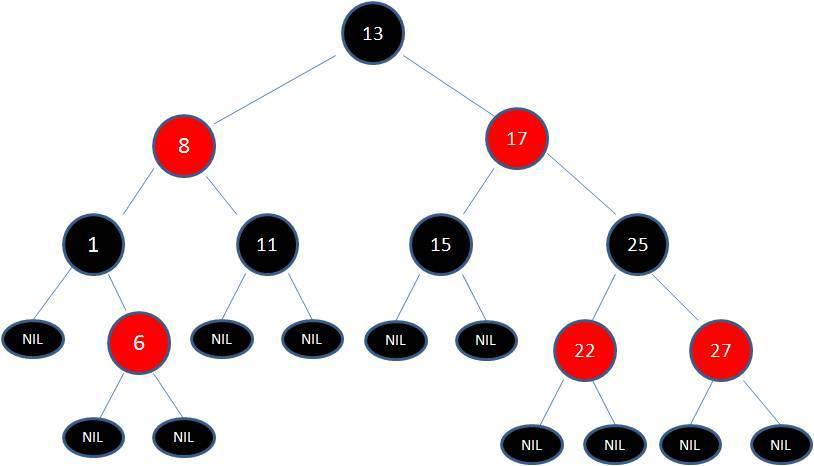
   一颗典型的红黑树：
   

操作

已经强调过，红黑树就是一颗特殊的二叉查找树，故查找也是借助二分的思想进行查找，操作和二叉查找树一致。

但是当进行插入和删除时势必会对红黑树的性质造成破坏。恢复红黑树的性质需要少量(O(log n))的颜色变更（实际是非常快速的）和不超过三次树旋转（对于插入操作是两次）。虽然插入和删除很复杂，但操作时间仍可以保持为O(log n)次。

前情提要

左旋转：右孩子替换父节点位置，父亲节点变为右孩子节点的左孩子。右孩子的左孩子变为父亲节点的右孩子。

右旋转：左孩子替换父亲节点的位置，父亲节点变为左孩子的右孩子。左孩子的右孩子变为父亲的左孩子。

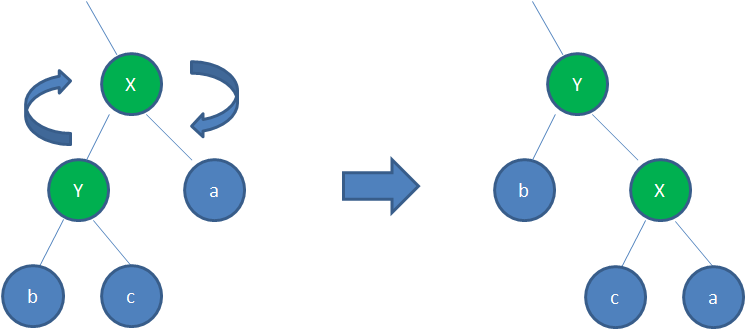
可证明左旋右旋不会破坏排序树的特点

插入

插入时首先以二叉查找树的方法增加节点并标记它为红色。

• 如果设为黑色，则会导致每个经过新节点的简单路径都会多一个黑色节点，对性质5的影响很大且不好调整
• 设为红色可能会导致出现连续两个红色节点而破坏规则4，但可以通过变换颜色和树旋转来进行调整。

插入操作时：

1. 在进行操作时性质一和性质三总是保持不被破坏
2. 性质4在增加红色节点，黑变红或者做旋转时被破坏
3. 性质5在增加黑色节点，红变黑或者做旋转时被破坏

首先，我们通过以下函数得到节点的祖父节点和叔叔节点

  node* grandparent(node *n){
       return n->parent->parent;
   }
  
   node* uncle(node *n){
       if(n->parent == grandparent(n)->left)
           return grandparent (n)->right;
       else
           return grandparent (n)->left;
   }

分情况讨论如下

新节点的父节点不为红色

情形一：新节点为根节点,没有父节点（空树或作为递归出口）

这种情况下只用把该节点变色为黑色满足性质2即可，对其它性质均无影响。

 void insert_case1(node *n){
     if(n->parent == NULL)
         n->color = BLACK;
     else
         insert_case2 (n);
 }

情形二：插入节点的父节点为黑色

插入节点没有子节点且父节点为黑不违反规则4，本身为红不违反任何规则5.不违反任何规则，不做任何修改。

 void insert_case2(node *n){
     if(n->parent->color == BLACK)
         return; /* 树仍旧有效*/
     else
         insert_case3 (n);
 }

新节点的父节点为红色

情形三：父节点和叔父节点都为红色

此时应该将父节点P和叔父节点U都变为红色，并将祖父节点变为黑色来维持性质5。（父节点和叔父节点同时变为黑色导致这两条简单路上的黑色节点多了1，将这两条简单路的交点祖父节点变为红色加回来），但祖父节点也有可能为根节点或者父节点为红。将祖父节点当做新插入的节点递归进行情形一即可。

 void insert_case3(node *n){
     if(uncle(n) != NULL && uncle (n)->color == RED) {
         n->parent->color = BLACK;
         uncle (n)->color = BLACK;
         grandparent (n)->color = RED;
         insert_case1(grandparent(n));
     }
     else
         insert_case5 (n);
 }

在下面的情况，假定父节点时祖父的右子节点。若是左子节点，下面情形中左右应该对调。

情形四

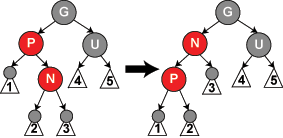
父节点P是红色而叔父节点U为黑色或缺少，新节点为父节点的左子节点。父节点P为祖父节点G的左孩子。（破坏了规则4--此时P，N为红，G为黑）

操作：

1. 对祖父节点进行一次右旋（P，N为红，G为黑） --破坏了规则4和规则5（G所在支路比N支路多一个黑色节点）；
2. 将G黑变红，P红变黑。（两支路黑色节点数一致，满足所有规则）
   

 void insert_case4(node *n){
     n->parent->color = BLACK;
     grandparent (n)->color = RED;
     if(n == n->parent->left && n->parent == grandparent(n)->left) {
         rotate_right(n->parent);
     } else {
         /* Here, n == n->parent->right && n->parent == grandparent (n)->right */
         rotate_left(n->parent);
     }
 }

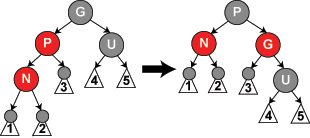
情形五

父节点P为红色，叔父节点U为黑色或者缺失。子节点N为P的右孩子，父节点为祖父节点的左孩子。（此时破坏了规则4。P，N红 ，G黑）
操作：

1. 对P节点进行一次左旋，（N，P为红，但此时P为N的左孩子）
2. 回到情形四，进行情形四的操作即可
   

 void insert_case5(node *n){
     if(n == n->parent->right && n->parent == grandparent(n)->left) {
         rotate_left(n);
         n = n->left;
     } else if(n == n->parent->left && n->parent == grandparent(n)->right) {
         rotate_right(n);
         n = n->right;
     }
     insert_case4 (n);
 }

删除

首先删除我们会碰到三种情况：

1. 待删除节点有两个非空儿子节点
2. 待删除节点有一个非空儿子节点
3. 待删除节点没有非空儿子节点

对于第一种情况，我们可以简单的将它转化为第二种情况，步骤如下

1. 找出左子树的最大值或者右子树的最小值N。
2. 将N复制覆盖到待删除节点
3. 删除N原来所在的节点（左子树中最大必定无右孩子，右子树中最小必定无左孩子）
   这样便转化成了第二种情况。
   第三种情况我们将随便一个空节点看作它的儿子
   所以我们只用讨论第二种情况。

我们使用以下代码来

待删除节点和它的孩子颜色不同

删除节点为红色

它的父亲和孩子一定为黑色，可以直接用它的孩子节点替换它，并不会破坏性质3，4。通过被删除节点的所有路径只是少了一个红色节点，这样可以继续保证性质5。

删除节点为黑色，它的孩子为红色

简单的用孩子顶替的话为破坏性质5，可以在顶替后将孩子换为黑色，这样可以继续保存性质5.

待删除节点和它的孩子颜色都为黑色

这种情况下，可以推断出该节点的两个孩子一定都是空节点。因为若其中一个儿子是黑色非叶子结点，另一个儿子是叶子结点，那么从该结点通过非叶子结点儿子的路径上的黑色结点数最小为2，而从该结点到另一个叶子结点儿子的路径上的黑色结点数为1，违反了性质5。

该情况比较复杂，分情况讨论

参考

1. 维基百科-红黑树
2. 程序员小灰-漫画红黑树