Codeforces好题选讲
CF575G
BFS + 贪心
2200*
我们可以发现，答案即为从终点到起点拼接组成的最小的十进制数字，设 \(s\) 为终点，\(t\) 为起点。
从 \(s\) 出发，我们可以贪心的进行决策，对于任意两条边，我们会优先比较哪条边离 \(t\) 更近，其次才是边权的大小，对于哪条边离终点更近，我们可以使用 BFS 预处理出来。
还有，我们发现边权可能会有 \(0\) ，也就是说我们需要将前导零所产生的贡献去掉。这时，我们可以想到从 \(s\) 出发，尽可能找边权为 \(0\) 的边进行扩展，对于扩展完的起点点集，选择其中距离 \(t\) 最近的点的点集出发即可，点到 \(t\) 的距离也可以使用 BFS 预处理出来。
最后在我们贪心寻找答案的途中，使用一个 \(pre\) 数组去记录上一个点的编号，方便最后我们输出方案。
const int N = 2e5+10;
const int inf = 0x3f3f3f3f;
#define pii std::pair<int,int>
#define fi first
#define se second
int n,m,diss[N],dist[N],pre[N];
std::vector<pii> E[N];
inline void solve()
{
fin >> n >> m;
for(int i = 1;i <= m;i++)
{
int u,v,w; fin >> u >> v >> w;
u++ , v++;
E[u].push_back({v,w});
E[v].push_back({u,w});
}
int s = n, t = 1;
memset(diss,0x3f,sizeof(diss));
memset(dist,0x3f,sizeof(dist));
std::queue<int> q;
q.push(t);dist[t] = 0;
while(!q.empty())
{
int u = q.front(); q.pop();
for(auto [v,w] : E[u])
if(dist[v] > dist[u] + 1)
{
dist[v] = dist[u] + 1;
q.push(v);
}
}
q.push(s);diss[s] = 0;
while(!q.empty())
{
int u = q.front(); q.pop();
for(auto [v,w] : E[u])
if(diss[v] > diss[u] + 1)
{
diss[v] = diss[u] + 1;
q.push(v);
}
}
q.push(s); pre[s] = n+1;
while(!q.empty())
{
int u = q.front(); q.pop();
for(auto [v,w] : E[u])
if(!w && !pre[v])
pre[v] = u, q.push(v);
}
if(pre[t])
{
fout << 0 << '\n';
int u = t;
std::vector<int> ans;
while(1)
{
ans.push_back(u);
if(u == s) break;
u = pre[u];
}
fout << ans.size() << '\n';
for(int x : ans) fout << x-1 << ' '; fout << '\n';
return ;
}
int sdis = inf;
for(int i = 1;i <= n;i++)
if(pre[i])
sdis = std::min(sdis,dist[i]);
std::vector<int> vec;
for(int i = 1;i <= n;i++)
if(pre[i] && dist[i] == sdis)
vec.push_back(i);
std::vector<int> path;
// 分层扩展
while(1)
{
pii cur = {inf,inf};
for(int u : vec)
for(auto [v,w] : E[u])
{
if(dist[v] > dist[u]) continue;
if(pre[v] && diss[pre[v]] < diss[u]) continue;
cur = std::min(cur,{dist[v],w});
}
path.push_back(cur.se);
std::vector<int> nxt;
for(int u : vec)
for(auto [v,w] : E[u])
{
if(dist[v] > dist[u]) continue;
if(pre[v] && diss[pre[v]] < diss[u]) continue;
if(dist[v] == cur.fi && w == cur.se)
{
nxt.push_back(v);
pre[v] = u;
}
}
for(int u : nxt)
if(u == t)
{
for(int x : path) fout << x; fout << '\n';
std::vector<int> ans;
while(1)
{
ans.push_back(u);
if(u == s) break;
u = pre[u];
}
fout << ans.size() << '\n';
for(int x : ans) fout << x-1 << ' '; fout << '\n';
return ;
}
vec = nxt;
}
}
CF269E
3100*
超级大分讨？暂时还没写，略。
CF323C
主席树
2400*
题单里最没意思的题，
考虑建可持久化权值线段树，设第二个排列的下标为版本，第二个排列的元素在第一个排列中出现的位置为下标。
答案就是版本 \(r_2\) 询问 \([l_1,r_1]\) 的值减去版本 \(l_1-1\) 询问 \([l_1,r_1]\) 的值。
const int N = 2e6+10;
struct node{
int ls,rs,sum;
}tr[N*40];
int rt[N],a[N],b[N],tot,c[N];
int p,n,m;
void modify(int &p,int q,int l,int r,int x)
{
p = ++tot; tr[p] = tr[q]; tr[p].sum++;
if(l==r) return ;
int mid = (l+r)>>1;
if(x <= mid) modify(tr[p].ls,tr[q].ls,l,mid,x);
else modify(tr[p].rs,tr[q].rs,mid+1,r,x);
}
int query(int p,int l,int r,int L,int R)
{
if(L <= l && r <= R) return tr[p].sum;
int mid = (l+r)>>1 , res = 0;
if(L <= mid) res += query(tr[p].ls,l,mid,L,R);
if(R > mid) res += query(tr[p].rs,mid+1,r,L,R);
return res;
}
int lst;
int f(int x){return (x+lst-1)%n+1;}
inline void solve()
{
fin >> n;
for(int i = 1;i <= n;i++) {fin >> a[i];c[a[i]] = i;}
for(int i = 1;i <= n;i++) {fin >> b[i];a[i] = c[b[i]];modify(rt[i],rt[i-1],1,n,a[i]);}
fin >> m;
for(int i = 1;i <= m;i++)
{
int l1,r1,l2,r2; fin >> l1 >> r1 >> l2 >> r2;
l1 = f(l1) , r1 = f(r1) , l2 = f(l2) , r2 = f(r2);
if(l1 > r1) std::swap(l1,r1);
if(l2 > r2) std::swap(l2,r2);
lst = query(rt[r2],1,n,l1,r1) - query(rt[l2-1],1,n,l1,r1);
fout << lst << '\n';
lst++;
}
}
CF264E
动态规划 + 线段树
3000*
显然，每次种树或者砍树时，最多只会有 \(10\) 个值变化，因为没有树的高是相同的。
考虑设计 DP 状态为以 \(i\) 为开头的 LIS 的长度，这样我们每进行一次操作最多就只会有 \(10\) 个值变化了。
接下来来考虑每棵树的高度，发现一棵树的高度可以表示为 ：
\[Initial\ height - The\ time\ of\ planting + Current \ time
\]
但是我们只会在相同时间下比较，所以上式可以化简为：
\[Initial\ height - The\ time\ of\ planting
\]
我们开两棵线段树，一棵线段树维护下标的最大 DP 值，另一棵线段树维护值域的最大 DP 值（因为值域有可能会扩展到负数，所以在计算时需要增加偏移量 \(\Delta\) )，再使用数组和集合来分别维护前 \(10\) 棵树以及高度为 \(1 \sim 10\) 的树的位置。
种树时，把高度小于当前树的树在线段树上删掉，插入新树后，我们再对刚刚已经删除了的树按照下标逆序计算新的 DP 值并插入。
砍树时，我们把要对应树前面的树删掉，删掉对应树后，我们同上再对刚刚删除了的树按照值域逆序计算新的 DP 值并插入。
const int N = 2e5+10;
const int M = 3e5+10;
const int pyl = 2e5;
int n,m;
#define ls u<<1
#define rs u<<1|1
class SegTree
{
public:
int L[M<<2],R[M<<2],val[M<<2];
void build(int u,int l,int r)
{
L[u]=l; R[u]=r;
val[u]=0;
if(l==r)return;
int mid = ((l+r)>>1);
build(ls,l,mid); build(rs,mid+1,r);
}
void modify(int u,int x,int w)
{
if(L[u]>x||R[u]<x)return;
if(L[u]==R[u])
{
val[u]=w;
return;
}
modify(ls,x,w); modify(rs,x,w);
val[u] = std::max(val[ls],val[rs]);
}
int query(int u,int l,int r)
{
if(L[u]>r||R[u]<l)return 0;
if(L[u]>=l&&R[u]<=r)return val[u];
return std::max(query(ls,l,r),query(rs,l,r));
}
}T1,T2;
#undef ls
#undef rs
int les_Tre[1010][2];
int tot, a[N],pos[N];
std::set<int> s;
int hs(int X){return X+pyl;}
inline void solve()
{
fin >> n >> m;
T1.build(1,1,M);
T2.build(1,1,M);
for(int i = 1;i <= m;i++)
{
int op,x; fin >> op >> x;
if(op == 1)
{
int y;fin >> y;
y = y+pyl-i;
pos[y] = x;
a[x] = y;
s.insert(x);
for(int j = std::max(1ll,y-9);j <= y-1;j++)
if(pos[j])
{
T1.modify(1,pos[j],0);
T2.modify(1,j,0);
}
for(int j = y;j >= std::max(1ll,y-9);j--)
if(pos[j])
{
int f = T1.query(1,pos[j]+1,M-5)+1;
T1.modify(1,pos[j],f);
T2.modify(1,j,f);
}
fout << T2.val[1] << '\n';
}
else
{
auto it = s.begin();
int sum = 1;
for(;sum <= x;it++,sum++)
{
T1.modify(1,*it,0);
T2.modify(1,a[*it],0);
}
--it;
int x = *it;
pos[a[x]] = 0;
a[x] = 0;
s.erase(x);
it = s.upper_bound(x);
if(it == s.begin())
fout << T2.val[1] << '\n';
else
{
do
{
it--;
int f = T2.query(1,a[*it]+1,M-5)+1;
T1.modify(1,*it,f);
T2.modify(1,a[*it],f);
}
while (it != s.begin());
fout << T2.val[1] << '\n';
}
}
}
}
CF251E
3000*
还没写，略。
CF257E
2200*
还没写，略。
CF297E
分类讨论 + 树状数组
3000*
分类讨论一下，发现只有，
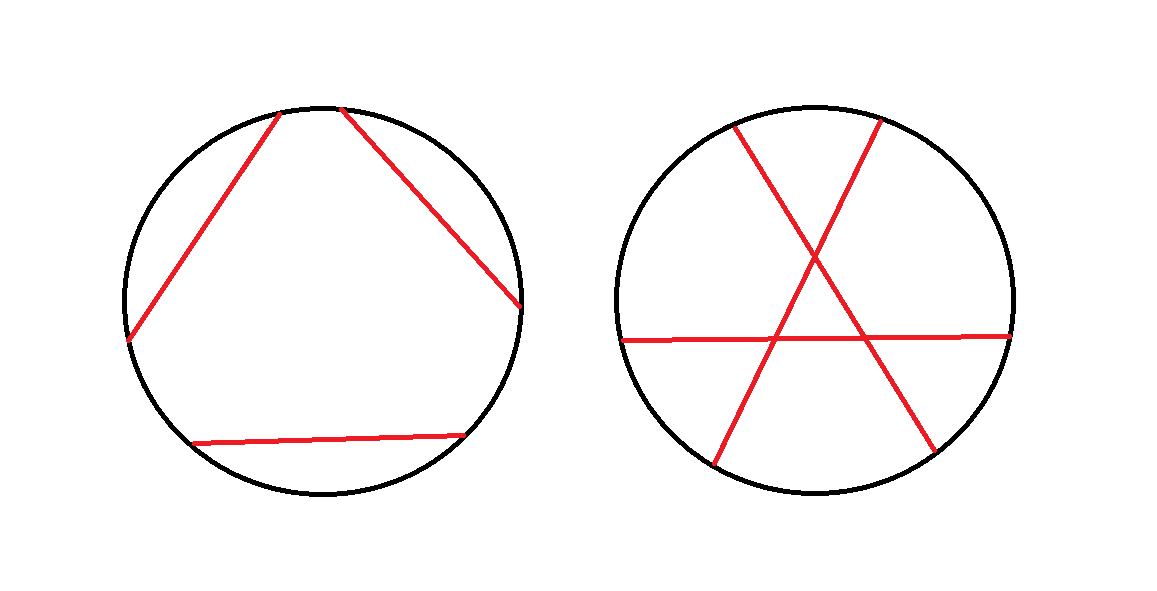
这两种位置关系能够满足题目要求。
发现求它们的方案数有点难，正难则反，我们考虑不满足关系的方案数。
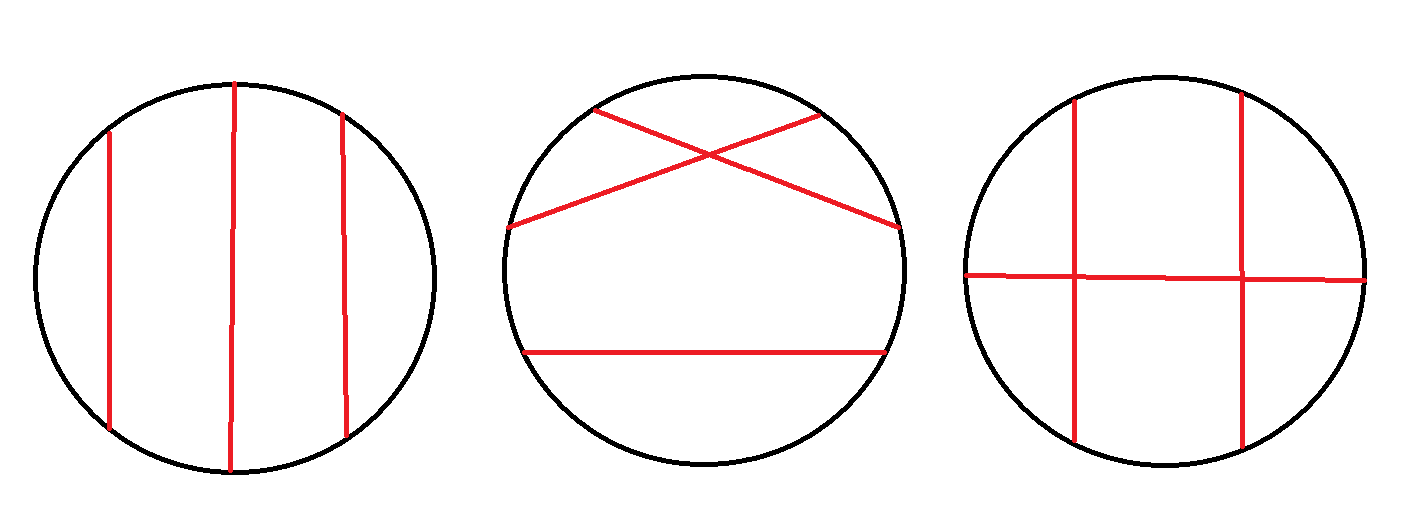
发现不满足要求的位置关系只有上面这几种（其实这就是这道题的困难所在了）。
总方案数为从 \(n\) 条弦里选出 \(3\) 条的方案数，也就是 \(C_n^3\)。
对于上面的第一张图，发现我们可以枚举每一条弦作为中间的那一条，只需要求出这条弦左右分别有多少条与它不相交的弦即可，也就是：
\[\sum^n_{i=1} l_i \times r_i
\]
对于上面的第二张图以及第三张图，我们发现它们的共同点，即为三条弦中有两条弦满足其余的两条弦一条与其相交，另外一条不与其相交。方案数即为：
\[\frac{\sum^n_{i=1}(l_i \times r_i)(n-l_i-r_i-1)}2
\]
(因为每张图都会有两条弦满足这个条件，所以还需要除以 \(2\))。
此时我们的问题变成了如何计算 \(l_i\) 以及 \(r_i\) 。
观察一下，我们发现若一条弦 \((x'y')\) 在当前这条弦 \((xy)\) 的左边，则需要满足：
\[[(x'<x ) \and (y'<x)] \or [(x'<x ) \and (y'>y)] \or [(x'>y ) \and (y'>y)]
\]
若一条弦在当前这条弦的右边，则需要满足：
\[[(x'>x ) \and (y'<y)]
\]
使用二维偏序处理即可。
const int N = 2e5+10;
struct node{int l,r,id;}a[N];
int l[N],r[N],n,tr[N];
void add(int x,int k){for(;x<=2*n;x+=x&-x)tr[x]+=k;}
int query(int x){int res=0;for(;x;x-=x&-x)res+=tr[x];return res;}
void init(){memset(tr,0,sizeof(tr));}
inline void solve()
{
fin >> n;
for(int i = 1;i <= n;i++)
{
fin >> a[i].l >> a[i].r;
if(a[i].l > a[i].r) std::swap(a[i].l,a[i].r);
a[i].id = i;
}
std::sort(a+1,a+1+n,[](node x,node y){
return x.l < y.l;
});
for(int i = 1;i <= n;i++)
{
l[a[i].id] += query(a[i].l) + query(n*2) - query(a[i].r);
add(a[i].r,1);
}
init();
for(int i = n;i >= 1;i--)
{
r[a[i].id] += query(a[i].r) - query(a[i].l);
add(a[i].r,1);
}
std::sort(a+1,a+1+n,[](node x,node y){
return x.r > y.r;
});
init();
for(int i = 1;i <= n;i++)
{
l[a[i].id] += query(n*2)-query(a[i].r);
add(a[i].l,1);
}
int res1 = n*(n-1)*(n-2)/6,res2 = 0;
for(int i = 1;i <= n;i++)
{
res1 -= l[i]*r[i];
res2 += (l[i]+r[i]) * (n-l[i]-r[i]-1);
}
fout << res1 - res2/2 << '\n';
}
浙公网安备 33010602011771号