博弈论

0.目录

本篇文章梳理如下

  1. 一些概念
  2. 经典模型——巴什博弈，威佐夫博弈
  3. 博弈点搜索
  4. 组合博弈
  5. \(\tt Nim\) 游戏以及其拓展
  6. 删边博弈
  7. 博弈点搜索+（\(alpha\) - \(beta\) 剪枝）
  8. 博弈论总结

1. 概念

博弈论

概述：多个人在一定约束条件下，利用已掌握的信息\(^{[1]}\)，使自身收益最大化的过程。全是抄的

公平

概述：每个人的操作是不是对等的。比如象棋就是不公平的，因为不能移动别人的棋子

信息对等

概述：每个人所掌握的信息是不是对等的。比如斗地主就是信息不对等的，因为你不知道别人手上的牌

\([1]\tt:\) 这是很重要的，因为有的题目你要站在当事人的角度分析，不能用旁观者的眼光对待。

2. 巴什博弈 & 威佐夫博弈

巴什博弈

题目：有 \(n\) 个石子，两个人轮流取，每次最多取 \(m\) 个，最少取 \(1\) 个，取完者获胜，问先手有没有必胜策略。

分析：作为大多数人都会的小奥题，它有一个很显然的解法：每次对方取 \(k\) 个，就取 \(m+1-k\) 个，第一次取 \(n\bmod(m+1)\) 个

显然：
\(\begin{cases}n\bmod(m+1)=0&\text{先手必败}\\n\bmod(m+1)\ne0&\text{先手必胜}\end{cases}\)

代码：

#include<stdio.h>
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    if(n % (m + 1)) printf("1");
    else printf("0");
    return 0;
}

威佐夫博弈

题目：有两堆石子，两个人轮流去，每次可以从一堆中取若干个或从两堆中取相同的若干个，取完者获胜，问先手有没有必胜策略。

分析：

Step 1.枚举

由于先手有必胜策略的情况多于没有的情况，于是我们来枚举少数的情况。（为了方便，默认第一堆数量小于等于第二堆）

先手没有必胜策略的情况有：\((0,0),(1,2),(3,5),(4,7),(6,10)\cdots\)

规律：记第 \(i\) 项为 \((a_i,b_i)\)，可得
\(a_0=b_0=0,a_i=\operatorname{mex}\{a_0,b_0,\dots,a_{i-1},b_{i-1}\},b_i=a_i+i,\operatorname{mex}\) 表示一个集合中最小没有出现过的自然数
于是任何自然数都一定包含在先手没有必胜策略的局面中（根据上文 \(\operatorname{mex}\) 规律可得）

通项公式下文再讲

Step 2.解法

如果给定一个局势 \((x,y)\)，如何判断是不是必胜状态呢？

用上面的式子应算显然不可能，我们要考虑通项公式

通项公式：记 \(\phi=\) 黄金比的倒数 \(=\dfrac{1+\sqrt5}{2}\)，则 \(a_i=\left\lfloor i\phi\right\rfloor,b_i=\left\lfloor i\phi^2\right\rfloor\)

于是代码如下：（威佐夫博弈模板）

#include<stdio.h>
#include<math.h>
int main(){
	int n,m,t;
	scanf("%d%d",&n,&m);
	if(n > m) t = n,n = m,m = t; // 保证n<m
	double phi = (1.000 + sqrt(5.000)) / 2.000; // 计算phi
	if(florr(phi * (m - n)) == n) printf("0"); // n=a[m-n]=floor(phi*(m-n))
	else printf("1");
	return 0;
}

3.博弈点搜索

对于前两个经典博弈例子，都有神奇的 \(O(1)\) 公式，但有没有涵盖大部分博弈的解法呢，答案是：有！！

而且，还是每天都给我们帮助，让我们受益匪浅的——DFS！！

惊不惊喜意不意外 不过标题似乎就说明了

我们把 DFS 递归走到的状态理解为一棵 DFS 树，树上的每一个节点都是一种状态，把它称之为\(\,\)博弈树（其实是一个 \(\rm{DAG}\)（有向无环图），但是我们把由不同方法到达的同一种状态看为不同节点，就会得到一棵树）

DFS 过程：把状态放到 DFS 函数的参数里，并且为每一种状态打上标记，还可以用记忆化搜索优化已经搜索过的节点。

那标记呢？标记分为 \(P\) 和 \(N\)

  • \(P:\text{Previous Position}\) 代表上一步的人赢，就是必败节点
  • \(N:\text{Now Position}\) 代表这一步的人赢，就是必胜节点

那我们怎么标记呢？\(\tt4\) 条规则 \(\downarrow\)

  1. 终止状态是 必败点
  2. 一步只能到达 必胜点 的都是 必败点
  3. 一步只能到达 必败点 的都是 必胜点
  4. 一步可以到达 必胜点 和 必败点 的也是 必胜点

或者概括一下 \(\downarrow\)

  1. 终止状态标记为 必败点
  2. 一步只能到达 必胜点 的都是 必败点
  3. 一步可以到达 必败点 的都是 必胜点

为什么呢？（这里我们以 威佐夫博弈 为例，其它自己推导不难）

证明 \(\texttt{1:}\) 威佐夫终止状态为 \((0,0)\)，是先手必败点。

证明 \(\texttt{2:}\) 定义这一堆为 \((a,b)\)

只取一堆。因为任何一个非 \(0\) 自然数只会在 \(a_i,b_i\) 中出现一次。如果 \(a=0\)，则 \(b=0\)，也是必败点。

两堆都取。如果两堆都取同样数量的石子，它们的差不变。而 \(b_i-a_i=i\)，不存在 \(i\ne j\)，使得 \(b_i-a_i=b_j-a_j\)。

证明 \(\texttt{3:}\) 定义这一堆为 \((a,b)\)

  • 如果 \(a=b\)，令 \(a\gets a-a,b\gets b-a\)，变成必败点 \((0,0)\)
  • 如果 \(a=a_i,b=b_i\)，不满足 \((a,b)\) 是必胜点
  • 如果 \(a=a_i,b\gt b_i\)，令 \(b\gets b_i\)，变成必败点 \((a_i,b_i)\)
  • 如果 \(a=a_i,b\lt b_i\)，令 \(a\gets a_{b-a},b\gets a_{b-a}+b-a\),变成必败点 \((a_{b-a},b_{b-a})\)
  • 如果 \(a\ne a_i\)，则一定 \(a=b_i\)，令 \(b\gets a_i\)，变成必败点 \((a_i,b_i)^{[2]}\)

\([2]:\) 根据 \(\operatorname{mex}\) 的定义，所有自然数都在 \(a_i,b_i\) 中出现过。

4.组合博弈

考虑一枚（或多枚）棋子，在一个 \(\mathrm{DAG}\)（有向无环图）中，两个人轮流将其进行移动 \(1\) 步，无法移动者输。

棋子可以理解为状态，有向无环图就是由不同的状态构成的有向无环图，移动就代表进入后继状态。

这里的博弈游戏中，定义 \(\operatorname{SG}\) 函数 \(\operatorname{SG}(x)=\operatorname{mex}\{\operatorname{SG}(y)\mid y\) 是 \(x\) 的后继状态集 \(\}\) （它的作用后面再说）

\(\operatorname{mex}\) 还是一个集合中最小没出现过的自然数

\(\operatorname{SG}\) 函数性质如下

  • \(\operatorname{SG}(\)终止节点\()=0\)（因为它的后继状态集是空集）
  • \(\operatorname{SG}(\)非终止节点\()\) 分两种情况来考虑
    1. \(\operatorname{SG}(x)=0\)，则 \(\operatorname{SG}(y)\ne0,y\) 是 \(x\) 的后继状态集
    2. \(\operatorname{SG}(x)\ne0\)，则存在 \(\operatorname{SG}(y)=0,y\) 是 \(x\) 的后继状态集

是不是和之前的必胜点和必败点有点像？其实对于一枚棋子移动的问题， \(\operatorname{SG}=0\) 就可以直接判断是必败点，反之为必胜点。

那如果是多枚棋子的移动呢？如果有 \(k\) 枚棋子，此时就会有 \(k\) 个局面 \(G_1,G_2,\dots,G_k\)，那么它们的和 \(G\) 满足 \(\operatorname{SG}(G)=\operatorname{SG}(G_1)\operatorname{xor}\operatorname{SG}(G_2)\cdots\operatorname{xor}\operatorname{SG}(G_k)\)

扯了这么多，\(\operatorname{SG}\) 函数，如何计算？

答案就是\(\,\)DFS（和上面那个不是一个东西，上面就是纯粹 DFS，\(\operatorname{SG}\) 函数说白了还是一些规律）。

代码：好的相信你已经会了（（

#include<stdio.h>
#include<string.h>
#include<vector>
const int maxn = 2001;
int SG[maxn],vis[maxn],n,m,k,ans = 0;
// SG就是当前的SG函数值
// vis[i]表示当前局面有没有SG值为i的节点，为了重复使用，让它记录上一次算出局面SG值为i的节点
std::vector<int> G[maxn]; // 图
void dfs(int x){
	if(SG[x] != -1) return;// 已经算过就不算了
	for(int i = 0;i < G[x].size();++i) dfs(G[x][i]);// 递归算子节点
	for(int i = 0;i < G[x].size();++i) vis[SG[G[x][i]]] = x;// 给SG值打上标记
	for(int i = 0;i <= n;++i) if(vis[i] != x){SG[x] = i;return;}// 最粗暴的mex计算方法
}
int main(){
	memset(SG,-1,sizeof SG);// 默认没算过
	memset(vis,-1,sizeof vis);// 默认为一个不存在的节点，0也行
	scanf("%d%d%d",&n,&m,&k);
	for(int i = 1;i <= m;++i){
		int u,v;
		scanf("%d%d",&u,&v);
		G[u].push_back(v);// 注意是有向图
	} 
	for(int i = 1;i <= k;++i){
		int x;
		scanf("%d",&x),dfs(x);// 每次都要dfs
		ans ^= SG[x];// 直接异或就可以了
	}
	if(ans) printf("win\n");
	else printf("lose\n");
	return 0;
}

5.Nim游戏

\(\tt{Nim}\) 游戏规则如下：

有 \(n\) 堆石子 \(a_1,a_2,\dots a_n\)，两人轮流从任意一组取若干个石子，谁取完谁赢，问先手有没有必胜策略。

解法：

\(\tt{Nim}\) 游戏作为组合博弈的一种，也有显然的 DFS \(\operatorname{SG}\) 函数解法，但是\(\,\)如果就这我还写这一类干嘛

更简单的方法
：\(\begin{cases}a_1\operatorname{xor}a_2\cdots\operatorname{xor}a_n=0&\text{先手必败}\\a_1\operatorname{xor}a_2\cdots\operatorname{xor}a_n\ne0&\text{先手必胜}\end{cases}\)

其中 \(\operatorname{xor}\) 表示异或运算 \(\oplus\)

证明：

这个解法成立需要满足三个条件：

  1. 终止状态是必败节点
  2. 由一个必败节点，无论怎么走都是必胜节点
  3. 由一个必胜节点，存在一种走法到必败节点

证明 \(\texttt{1:}\) 因为必败态 \(0\operatorname{xor}\cdots0=0\)，所以成立

证明 \(\texttt{2:}\) 记我们要取的是第 \(i\) 堆，根据 异或 的性质，可得

\[a_1\operatorname{xor}a_2\cdots\operatorname{xor}a_{i-1}\operatorname{xor}a_{i+1}\cdots\operatorname{xor}a_n=a_i \]

而只有 \(a_i\operatorname{xor}a_i=0\) ，所以无论把 \(a_i\) 改成什么，都得不到必败状态

证明 \(\texttt{3:}\) 如果 \(a_1\operatorname{xor}a_2\cdots\operatorname{xor}a_n=x\)，此时可以找到一个 \(a_i\)，\(a_i\) 在 \(x\) 的最高二进制位上是 \(1\)，那么 \(a_i\operatorname{xor}x\ge0\)，于是令 \(a_i\gets a_i\operatorname{xor}x\) 即可

\(\tt Nim\) 游戏模板

代码：

#include<stdio.h>
int main(){
	int T;
	scanf("%d",&T);
	while(T--){
		int n,res = 0;
		scanf("%d",&n);
		for(int i = 1;i <= n;++i){
			int ai;
			scanf("%d",&ai);
			res ^= ai;
		}
		if(res) puts("Yes");
		else puts("No");
	}
	return 0;
}

Anti-Nim 游戏

规则：与 \(\tt{Nim}\) 一样，不过是取完者败。

于是我们脑袋里出现一个显然的思路：把上一份代码 Yes 和 No 反过来。不过你以为就会这么简单？

假如有一堆，两个石子，如果用如上思路，先手直接取两个然后自己让自己输掉。但最佳策略应该是先取一个让对方输掉。

结论：

  1. 石子堆数异或和 \(=0\) 且每堆只有 \(1\) 个石子为必胜状态
  2. 石子堆数异或和 \(\ne0\) 且至少一堆石子个数大于 \(1\) 为必胜状态
  3. 其余都是必败状态

证明：

证明 \(\texttt{1:}\) 只有偶数堆 \(1\) 才能异或得 \(0\)，两人每次取一堆，后手取最后一堆，先手必胜。

证明 \(\texttt{2,3:}\)

只有一堆石子个数大于 \(1\)（情况 \(\tt2_1\))

  • 有偶数堆 \(1\)，可以把大于 \(1\) 这堆取完，那么就会剩下奇数堆 \(1\)，再加上是后手先走，先手必胜。
  • 有偶数堆 \(1\)，如果想异或和为 \(0\)，剩下那堆必须为 \(0\)，不可能
  • 有奇数堆 \(1\)，可以把大于 \(1\) 这堆取得剩下 \(1\) 个，那么就会剩下奇数堆 \(1\)，再加上后手先走，先手必胜。
  • 有奇数堆 \(1\)，如果想异或和为 \(0\)，剩下那堆必须为 \(1\)，矛盾

于是定理 \(\tt2\) 得到证明。

有多堆石子个数大于 \(1\)（情况 \(\tt{2_2}\texttt{,3}\)）

  • 异或和为 \(0\)，此时随便怎么走都会转化为异或和不为 \(0\) 的状态。那么一定可以转化为两种情况
  1. 有大于等于两堆的石子个数 \(\gt1\)，变成下面的情况 \(\tt3\downarrow\)。
  2. 有一堆石子个数 \(\gt1\)，这就是已证的定理 \(\tt{2_1}\)。
  • 异或和不为 \(0\)，此时根据 \(\tt Nim\) 的证明，必然存在一种变成异或和为 \(0\) 的走法。（这是情况 \(\tt3\)）

原题

代码：

#include<stdio.h>
int main(){
	int T;
	scanf("%d",&T);
	while(T--){
		int n,res = 0,cnt = 0;
		scanf("%d",&n);
		for(int i = 1;i <= n;++i){
			int x;
			scanf("%d",&x);
			res ^= x,cnt += x > 1;
		}
		if(res == 0 && cnt == 0) puts("John");
		else if(res && cnt) puts("John");
		else puts("Brother");
	}
	return 0;
}

S-Nim

这个名字来源于 一道题。

题意：\(\tt{Nim}\) 游戏，但是每次可以取的石子数量必须是 \(s_1,s_2,\cdots,s_k\) 中的一个。

解法：这题没有 \(O(1)\) 解法，于是直接 DFS \(\operatorname{SG}\) 值即可。

注意两点优化：

  1. 先把 \(s\) 数组排好序，这样 DFS 的时候，找到 \(s_i>x\) 就直接退出，节省时间
  2. 每 \(m\) 组测试样例并不是相互独立的（因为这 \(m\) 组数据的步数集都是相同的），可以在读入样例的开头先把 \(\operatorname{SG}\) 数组清空为 \(-1\)。（这卡了我好久）

放代码：

#include<stdio.h>
#include<string.h>
#include<algorithm>
inline int Read(){
    register int x = 0,f = 1,c = getchar();
    for(;c < 48 || c > 57;c = getchar()) f = c == 45 ? -1 : 1;
    for(;c >= 48 && c <= 57;c = getchar()) x = x * 10 + (c ^ 48);
    return x * f;
}
int SG[10001],step[101],vis[10001],n,m,k,ans = 0;
void dfs(int x){
	if(SG[x] != -1) return;
	for(int i = 1;i <= k && step[i] <= x;++i) dfs(x - step[i]);
	for(int i = 1;i <= k && step[i] <= x;++i) vis[SG[x - step[i]]] = x;
	// 注意上面的 step[i] <= x，可以节省时间（因为排了序在step[i]不行时直接退出循环）
	for(int i = 0;;++i) if(vis[i] != x){SG[x] = i;return;}
}
int main(){
	while(k = Read()){
		for(int i = 1;i <= k;++i) step[i] = Read();
		std::sort(step + 1,step + k + 1);// 排序！！
		m = Read();
		memset(SG,-1,sizeof SG);// 在m组数据开头清空即可
		while(m--){
			ans = 0,n = Read();
			for(int i = 1;i <= n;++i){
				int x = Read();
				dfs(x);
				ans ^= SG[x];
			}
			if(ans) putchar('W');
			else putchar('L');
		}
		putchar('\n');
	}
	return 0;
}

6. 删边博弈

Easy VERSION

什么毒瘤题，还分 Easy Vision

题目：给定一棵有根树，两个人轮流从树上删边，每删一条边，不与根相连的一部分也会被删去，谁不能再删谁输，问先手有没有必胜策略。

结论：叶子结点的 \(\operatorname{SG}\) 函数值为 \(0\)，其它的节点的 \(\operatorname{SG}\) 函数值为其所有子节点的 \(\operatorname{SG}\) 值 \(+1\) 后的异或和

Q.这么奇葩的结论，怎么让我想？

A. 可以先写 DFS，然后再分析找规律。

注意：学会用 DFS（也就是前文的博弈点搜索）是非常重要的解题方法，你甚至还可以自己模拟搜索。

让我们来看看如何这条定理证明

数学归纳法证明如下：

一：只有一个或两个节点时显然成立

这个很显然，只有一个节点，其 \(\operatorname{SG}\) 值就是 \(0\)，是必败节点，对的。

有两个节点，\(\operatorname{SG}(rt)=1,\operatorname{SG}(lf)=0\)，那么 \(rt\) 是必胜节点，\(lf\) 是必败节点。

二：当点数不超过 \(n\) 时定理成立，\(n+1\) 个节点定理也成立

两种情况：

根节点有一个儿子 \((1)\)

根节点不止一个儿子 \((2)\)

\((1):\) 假设树长这个样子：

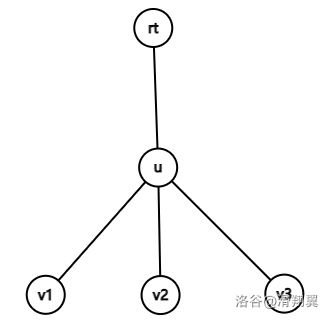
设这棵树为 \(T_\text{原}\)，删边后 \(T\)，\(T_\text{原}\) 以 \(u\) 为根的子树为 \(T'\)。

删一条边，也分两种情况

  • 删边 \(\{rt,u\}\)，此时只剩下根节点，\(\operatorname{SG}(T)=0\)
  • 删 \(T'\) 中的一条边 \(E\)，此时因为删边后点数会小于 \(n\)，所以此时定理成立，那么 \(\operatorname{SG}(rt)=\operatorname{SG}(u)+1\)。

那 \(\operatorname{SG}(u)\) 的范围是多少呢？

设 \(\operatorname{SG}(u)=k\)，则 \(T'\) 的后继局面中的 \(\operatorname{SG}\) 值必定包含了 \(\left[0,k\right)\) 的所有自然数，范围就是 \(0\sim k-1\)（因为一个局面的 \(\operatorname{SG}\) 值等于其后继局面 \(\operatorname{SG}\) 值的 \(\operatorname{mex}\)）。所以 \(\operatorname{SG}(T)\) 可以取遍 \(1\sim k\)。

算上第一种情况，删边后 \(\operatorname{SG}(rt)\) 的范围是 \(0\sim k\)，取遍了 \(\le k+1\) 的自然数，于是删边前 \(\operatorname{SG}(rt)=k+1\)

于是 \(\operatorname{SG}(rt)=\operatorname{SG}(u)+1\) 得证。

\((2):\) 此时的图可以拆成若干个根节点相同但 \(u\) 不同的和上图相同的树，此时就和 \(\tt{Nim}\) 一样，异或起来即可。

Hard VERSION

最毒瘤的东西来了。。。

题面完全一样，只不过树变成了一个图。只能放定理了：

\(\sf{F\color{red}usion\text{ }Principle}\) 定理如下：

把图中任意一个偶长度环缩成一个新点，任意一个奇长度环缩成一个新点加一条边，所有连到原先环上的边全部改为与新点相连。这样的改动不会影响图的 \(\operatorname{SG}\) 值

证明是什么？我不会

事实上这种题考的挺偏，而且一出就是板子，在 \(\texttt{NOI}\) 赛场上也几乎不可能碰到。

7. 博弈点搜索+

之所以这样安排顺序，是因为这个东西有相比起普通的博弈点搜索难不止亿点点。

极大极小搜索 & \(alpha\) - \(beta\) 剪枝

来看一个栗子：

题目：给定一个图，图上包含一些虚边和实边，两个人轮流每次把一条虚边变成实边，这个人的得分就会加上新产生的三角形数。

Pay Attention： 这只是其中一个栗子，\(\alpha\) - \(\beta\) 剪枝可以概括为：两个人博弈，甲想让自己的利益最大化，乙想让甲的利益最小化。

分析：

这种题没有技巧，只能爆搜。但这并不影响我们在爆搜时使用技巧！！

DFS 技巧，常用的就是\(\,\)记忆化搜索，可行性剪枝，最优性剪枝。

记忆化显然不可能，可行性剪枝放到这里来是什么鬼（（？？于是考虑最优性剪枝。

假如选一个点，并且定义去这个点后甲的得分减去乙的得分为 \(f(x)\)。作为甲，希望它最大；作为乙，希望它最小，于是定义 \(\max(f)=\alpha,\min(f)=\beta\)（点题的写作手法）

再来定义甲的局面为 \(max\) 局面，乙的局面为 \(min\) 局面。

考虑这一步到甲，是 \(max\) 局面，显然这个局面会继承上一步的 \(\beta\)，而甲会把它走成 \(\alpha\) 的情况。

但是如果 \(\alpha(now)>\beta(prev)\)，说明这条路线不是最优，\(prev\) 的其它后继状态也可以不用再搜了。

为什么？说白点，这个局面满足以下条件之一

乙想让甲得分更小，甲却得到了比乙给甲的最小得分还大的得分；这时乙本可以给甲更小的得分，原来的方案不是最优方案。

又或者甲想让自己得分尽量大，却给乙一个比甲现在得分要少的局面；显然这让自己得分更少，原来的方案也不是最优方案。

两个不都是一样的吗

但是这种东西你需要两方都去考虑 虽然让自己利益最大就等于让别人利益最小

经过剪枝，最后剩下的都是最优决策。

于是这种搜索叫极大极小搜索，这种剪枝叫做 \(alpha\) - \(beta\) 剪枝。（呼应开头，画龙点睛）

8. 总结

博弈论这种东西，可以分类为：

  1. 巴什博弈、威佐夫博弈、\(\tt Nim\) 以及 \(\texttt{Anti-Nim}\) ，这种东西有 \(O(1)\) 公式，其余大部分都没有
  2. 用到 \(\operatorname{SG}\) 函数的游戏（包括大部分 \(\tt Nim\) 拓展）：运用 \(\operatorname{SG}\) 函数 DFS 计算方法，牢记 \(\operatorname{mex}\)。
  3. 博弈点搜索以及其拓展 极大极小搜索 ：前者有可能用到，记忆化搜索，后者有专门的最优性剪枝

qq_emoji: cy

posted @ 2021-06-28 21:15  One_Zzz  阅读(685)  评论(4)    收藏  举报