算法第四章上机实验报告

算法第四章上机实验报告

一．实践题目名称： 删数问题

二．问题描述：给定n位正整数a，去掉其中任意k≤n 个数字后，剩下的数字按原次序排列组成一个新的正整数。对于给定的n位正整数a和正整数 k，设计一个算法找出剩下数字组成的新数最小的删数方案。如果数字最前面有0不输出。

输入格式：

第 1 行是1 个正整数 a。第 2 行是正整数k。

输出格式:

输出最小数。

 

 

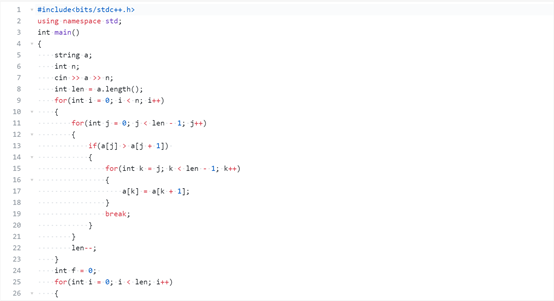
三．贪心选择策略：将正整数每个位数分别存入数组，从高位到低位来循环，如果第i个数大于第i+1个数，则删除第i个数，如果循环结束删除数小于k，则从数组最后开始删除直到删除总数为k个。然后输出数组，若数组开头为‘ 0 ’则不输出‘ 0 ’。

 代码如下:

 

 

 

四．时间复杂度分析

删除数循环时间复杂度为O（m*k）; 输出数组的时间复杂度为O（m-k）

所以，算法的时间复杂度为O（m*k）.

五．对贪心算法的理解

贪心算法的基本要素为最优子结构性质和贪心选择性质（某种意义的局部最优）。

贪心算法指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有利)的选择，从而希望能够导致结果是最好或者最优的算法。

算法所得到的结果不一定是最优的结果，但是都是相对接近最优解的结果。