多项式回归

原有数据特征下新增维度

# 数据
import numpy as np
import matplotlib.pyplot as plt
​
x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.5*x**2+x+2+np.random.normal(0,1,size=100)
​
plt.scatter(x,y)
plt.show()
 
 
 
 
 
# 线性回归
from sklearn.linear_model import LinearRegression
​
lr = LinearRegression()
lr.fit(X,y)
Y =lr.predict(X)
plt.scatter(x,Y,color='y')
plt.scatter(x,y)
plt.show()
print("训练准确度：",lr.score(X,y))

　

 
 
训练准确度： 0.41533504201014526
 

解决方案，添加一个特征

X2 = np.hstack([X,X**2])
X2.shape
​
lr2 = LinearRegression()
lr2.fit(X2,y)
Y =lr2.predict(X2)
# plt.scatter(x,Y,color='y')
plt.scatter(x,y)
plt.plot(np.sort(x),Y[np.argsort(x)],color='r')
plt.show()
 
 

scikit-learn 中调用多项式回归

 
import numpy as np
import matplotlib.pyplot as plt
​
x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.5*x**2+x+2+np.random.normal(0,1,size=100)
​
# 升维
from sklearn.preprocessing import PolynomialFeatures
​
poly = PolynomialFeatures(degree=2)
poly.fit(X)
X3 = poly.transform(X)
print(X3.shape)
print(X3[:5,:])
print(X[:5,:])
 
 
 
>>>(100, 3)
>>>[[ 1.          2.82741507  7.99427598]
 [ 1.          1.11916321  1.25252628]
 [ 1.         -1.97857993  3.91477853]
 [ 1.         -1.74809423  3.05583345]
 [ 1.          0.4303255   0.18518004]]
>>>[[ 2.82741507]
 [ 1.11916321]
 [-1.97857993]
 [-1.74809423]
 [ 0.4303255 ]]

　　

from sklearn.preprocessing import StandardScaler
​
# 均值标准差归一化
std = StandardScaler()
std.fit(X3)
X3 = std.transform(X3)
 
 
# 模型
lr3 = LinearRegression()
lr3.fit(X3,y)
Y =lr3.predict(X3)
# plt.scatter(x,Y,color='y')
plt.plot(np.sort(x),Y[np.argsort(x)],color='r')
plt.scatter(x,y)
plt.show()
print("训练准确度：",lr3.score(X3,y))

　　

 
 
训练准确度： 0.7783886413124025
 

Pipeline

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
​
poly_reg = Pipeline([
    ("ploy",PolynomialFeatures(degree=2)),
    ("stdScaler",StandardScaler()),
    ("lin_reg",LinearRegression())
])
​
poly_reg.fit(X,y)
Y = poly_reg.predict(X)
plt.scatter(x,Y,color='y')
plt.scatter(x,y)
plt.show()

　　

 
 
 

过拟合和欠拟合

 

欠拟合：算法所训练的模型不能完整表述数据关系
过拟合：算法所训练的模型过多的表达了数据间的噪音关系

 

 

 
 
 
def predict(degree):
    poly_reg = Pipeline([
    ("ploy",PolynomialFeatures(degree)),
    ("stdScaler",StandardScaler()),
    ("lin_reg",LinearRegression())
])
    return poly_reg
 
 
 
 
from sklearn.model_selection import train_test_split
​
trainX,testX,trainY,testY = train_test_split(X,y)
p = predict(2)
p.fit(trainX,trainY)
print("训练集误差:",p.score(trainX,trainY))
print("测试集误差",p.score(testX,testY))
print("=="*10)
trainX,testX,trainY,testY = train_test_split(X,y)
p = predict(13)
p.fit(trainX,trainY)
print("训练集误差:",p.score(trainX,trainY))
print("测试集误差",p.score(testX,testY))
print("=="*10)
trainX,testX,trainY,testY = train_test_split(X,y)
p = predict(100)
p.fit(trainX,trainY)
print("训练集误差:",p.score(trainX,trainY))
print("测试集误差",p.score(testX,testY))
 
 
 
训练集误差: 0.8693910420620271
测试集误差 0.8629785719882223
====================
训练集误差: 0.8969676964385225
测试集误差 0.8209727026124418
====================
训练集误差: 0.9191183389946399
测试集误差 -296704122331898.1
 
学习曲线：随着训练样本的逐渐增多，算法训练出的模型的表现能力

 
 
 
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
​
trainX,testX,trainY,testY = train_test_split(X,y)
​
trainScore = []
testScore = []
for i in range(1,trainX.shape[0]+1):
    lr = LinearRegression()
    lr.fit(trainX[:i],trainY[:i])
    y_train_predict = lr.predict(trainX[:i])
    trainScore.append(mean_squared_error(trainY[:i],y_train_predict))
    y_test_predict = lr.predict(testX)
    testScore.append(mean_squared_error(testY,y_test_predict))
 
 

 
plt.plot([i for i in range(1,76)],np.sqrt(trainScore),label="train")
plt.plot([i for i in range(1,76)],np.sqrt(testScore),label="test")
plt.legend()
plt.show()

　　

 
 
 

测试数据集的意义

  1. 训练数据集：训练模型
  2. 验证数据集：调整超参数用的数据集
  3. 测试数据集：作为衡量最终模型的性能的数据集
 

交叉验证

 

import numpy as np
from sklearn import datasets
 
 
digits = datasets.load_digits()
x = digits.data
y = digits.target
 
 
 
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
​
trainX,testX,trainY,testY = train_test_split(x,y)
 

best_score,best_p,best_k = 0,0,0
for k in range(2,11):
    for p in range(1,6):
        knn_clf = KNeighborsClassifier(weights="distance",n_neighbors=k,p=p)# p是明可夫斯基距离
        knn_clf.fit(trainX,trainY)
        score = knn_clf.score(testX,testY)
        if score>best_score:
            best_score,best_p,best_k = score,p,k
print("best_score:",best_score)
print("best_p:",best_p)
print("best_k:",best_k)
 
 
 
best_score: 0.9844444444444445
best_p: 2
best_k: 2
 
使用交叉验证
 
 
from sklearn.model_selection import cross_val_score
​
knn_clf = KNeighborsClassifier() 
cross_val_score(knn_clf,trainX,trainY)
 

>>>array([0.98896247, 0.97767857, 0.97982063])
 
 
 
 
best_score,best_p,best_k = 0,0,0
for k in range(2,11):
    for p in range(1,6):
        knn_clf = KNeighborsClassifier(weights="distance",n_neighbors=k,p=p)# p是明可夫斯基距离
        scores = cross_val_score(knn_clf,trainX,trainY,cv=5) # 默认分为3份
        score = np.mean(scores)
        if score>best_score:
            best_score,best_p,best_k = score,p,k
print("best_score:",best_score)
print("best_p:",best_p)
print("best_k:",best_k)
 
 
 >>>
best_score: 0.987384216020246
best_p: 5
best_k: 5


 
best_knn_clf = KNeighborsClassifier(n_neighbors=5,p=5,weights="distance")
best_knn_clf.fit(trainX,trainY)
best_knn_clf.score(testX,testY)
 
 

>>>0.9733333333333334

　　

 

偏差和方差

 

 

模型正则化

 

岭回归 和 Lasso回归

 

import numpy as np
import matplotlib.pyplot as plt
​
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
​
x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.5*x**2+x+2+np.random.normal(0,1,size=100)
​
def LinRegression(degree):
    poly_reg = Pipeline([
    ("ploy",PolynomialFeatures(degree)),
    ("stdScaler",StandardScaler()),
    ("lin_reg",LinearRegression())
])
    return poly_reg
​
def plot_model(x,y1,y2):
    x = x.reshape(-1)
    plt.scatter(x,y1)
#     plt.scatter(x,y2,color='r')
    plt.plot(np.sort(x),y2[np.argsort(x)],color="y")
    plt.show()
 

 
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
​
trainX,testX,trainY,testY = train_test_split(X,y)

　　

 
 
 

一般多项式回归

from sklearn.metrics import mean_squared_error
​
poly_reg = LinRegression(20)
poly_reg.fit(trainX,trainY)
​
y_predict0 = poly_reg.predict(trainX)
y_predict = poly_reg.predict(testX)
print(mean_squared_error(testY,y_predict))
​
# 绘图
plot_model(trainX,trainY,y_predict0)
 
 
 
>>>0.9086483532915508

　　

 
 

使用岭回归

from sklearn.linear_model import Ridge
​
def RidgeRegression(degree,alpha):
    poly_reg = Pipeline([
    ("ploy",PolynomialFeatures(degree)),
    ("stdScaler",StandardScaler()),
    ("ridge_reg",Ridge(alpha))
])
    return poly_reg
 

 
 
ridge_reg = RidgeRegression(20,0.0001)
ridge_reg.fit(trainX,trainY)
​
y_predict0 = ridge_reg.predict(trainX)
y_predict = ridge_reg.predict(testX)
​
print(mean_squared_error(testY,y_predict))
plot_model(trainX,trainY,y_predict0)
 
 
 
>>>1.072090145136618
 


 
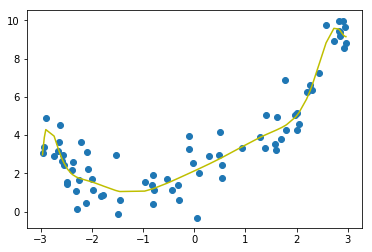
ridge_reg = RidgeRegression(20,1000)
ridge_reg.fit(trainX,trainY)
​
y_predict0 = ridge_reg.predict(trainX)
y_predict = ridge_reg.predict(testX)
​
print(mean_squared_error(testY,y_predict))
plot_model(trainX,trainY,y_predict0)
 
 
 
>>>4.129925110597825

　　

 

 

 

lasso回归

from sklearn.linear_model import Lasso
​
def LassoRegression(degree,alpha):
    poly_reg = Pipeline([
    ("ploy",PolynomialFeatures(degree)),
    ("stdScaler",StandardScaler()),
    ("lasso_reg",Lasso(alpha))
])
    return poly_reg
 
 
 
lasso_reg = LassoRegression(20,0.01)
lasso_reg.fit(trainX,trainY)
​
y_predict0 = lasso_reg.predict(trainX)
y_predict = lasso_reg.predict(testX)
print(mean_squared_error(testY,y_predict))
plot_model(trainX,trainY,y_predict0)
 
 
 
>>>1.074005662099316

　　

 
 

弹性网

 

 

posted @ 2018-07-20 14:06  家迪的家  阅读(422)  评论(0)    收藏  举报