【数据结构与算法】2 - 5 二叉查找树、平衡二叉树与红黑树
§2-5 二叉查找树、平衡二叉树与红黑树
2-5.1 二叉查找树(Binary search tree)
定义:二叉查找树,又称二叉排序树或二叉搜索树。其中任意一个结点左子树上的值都小于当前结点,任意一个结点右子树上的值都大于当前结点。
数据存储过程:小的存左边,大的存右边,一样则不存。
数据查找过程:从根结点开始,比较结点的数值。若比当前结点小,则前往左子结点;若比当前结点大,则前往右子结点;直至找到或前往空结点为止。
二叉树的遍历方式:二叉树有四种遍历方式,以下图所示的二叉查找树为例
- 前序遍历:从根结点开始,依次按照当前结点、左子结点、右子结点的顺序遍历;遍历结果为
20, 18, 16, 19, 23, 22, 24; - 中序遍历:从根结点开始,依次按照左子结点、当前结点、右子结点的顺序遍历;遍历结果为
16, 18, 19, 20, 22, 23, 24; - 后序遍历:从根结点开始,依次按照左子结点、右子结点、当前结点的顺序遍历;遍历结果为
16, 19, 18, 22, 24, 23, 20; - 层序遍历:从根结点开始,一层一层地遍历;遍历结果为
20, 18, 23, 16, 19, 22, 24;
弊端:当二叉查找树的左右子树高度不一致时,查找效率会变低,极端情况下,查找树会退化成一个链表。为解决这一问题,可使用平衡二叉树。
2-5.2 平衡二叉树(Balanced binary tree)
定义:平衡二叉树也是一种二叉查找树,但是任意结点左右子树高度差不超过 1,即任一结点的左右子树都是平衡二叉树。
平衡二叉树也称为 AVL 树,该名字源于平衡二叉树的发明者 G. M. Adelson-Velsky 和 Evgenii Landis。
平衡二叉树在每次添加结点和删除结点时都需要考虑树的平衡情况,为方便起见,先介绍有关概念。
- 平衡因子(balance factor, BF):左右子树高度差定义为平衡因子。若 BF 的绝对值大于 1 时,平衡二叉树失衡;
- 最小不平衡子树:距离插入结点最近的,且 BF 绝对值大于 1 的结点为根结点的子树。对于这样的子树,通过旋转即可恢复平衡。
旋转机制:添加一个结点之后,该树不再是一棵平衡二叉树时,触发旋转机制,旋转最小不平衡子树。共有两种旋转方式。
在旋转前,首先要确定失衡支点:从添加的结点开始,找到距离该结点最近的,且 BF 绝对值大于 1 的根结点的子树。
- 左旋:左旋有两种情况,简单左旋如下图所示:
若根结点右子树具有左子树,则情况复杂些,如下图所示:
-
右旋:右旋同样也存在两种情况,简单右旋如下图所示:
若根结点左子树具有右子树,则情况复杂些,如图所示:
平衡二叉树需要旋转的四种情况:插入新结点后,原平衡树失衡,根据新结点与形成的最小不平衡树的根结点的位置,有以下四种不同的旋转情况:
-
左左:新结点位于根结点左子树的左子树上,进行一次右旋:
-
左右:新结点位于根结点左子树的右子树上,先局部左旋,再右旋:
-
右右:新结点位于根结点右子树的右子树上,进行一次左旋:
-
右左:新结点位于根结点右子树的左子树上,先局部右旋,再左旋:
弊端:添加结点时,过于繁琐的旋转的开销较大,可以使用红黑树解决这一问题。
2-5.3 红黑树(Red-black tree)
定义:红黑树是一种自平衡的二叉查找树。红黑树是一种特殊的二叉查找树,树上的每一个结点都有存储位表示结点的颜色。
特点:每一个结点要么为红,要么为黑;红黑树不是高度平衡的,其平衡通过红黑规则实现,其增删改查的性能表现较好。
红黑规则:
-
每一个结点要么为红色,要么为黑色;
-
根结点必须为黑色;
-
若一个结点无子结点或父结点,则该结点相应的指针的值为
Nil,这些Nil视为叶结点,每个叶结点(Nil)是黑色的;这意味着,
Nil结点在实际上是存在的,但是其数据为空,位于叶结点中,在遍历与查找当中意义不大; -
若某一结点为红色,其子结点必须为黑色(即两个红色结点不能相连);
-
对每一个结点,从该结点到所有后代叶结点的简单路径上,均包含相同数目的黑色结点;
后代:该结点的所有子结点称为该结点的后代;
叶结点:无子结点的结点称为叶结点;后代叶结点指的是所有为叶结点的子结点;
简单路径:不重复经过同一顶点的通路;
红黑树示意图:
添加结点的规则:
- 添加结点的默认颜色为红色,效率更高,调整次数更少;
- 进行旋转时忽略
Nil结点,旋转完毕后将Nil补全;
添加规则如下图所示:
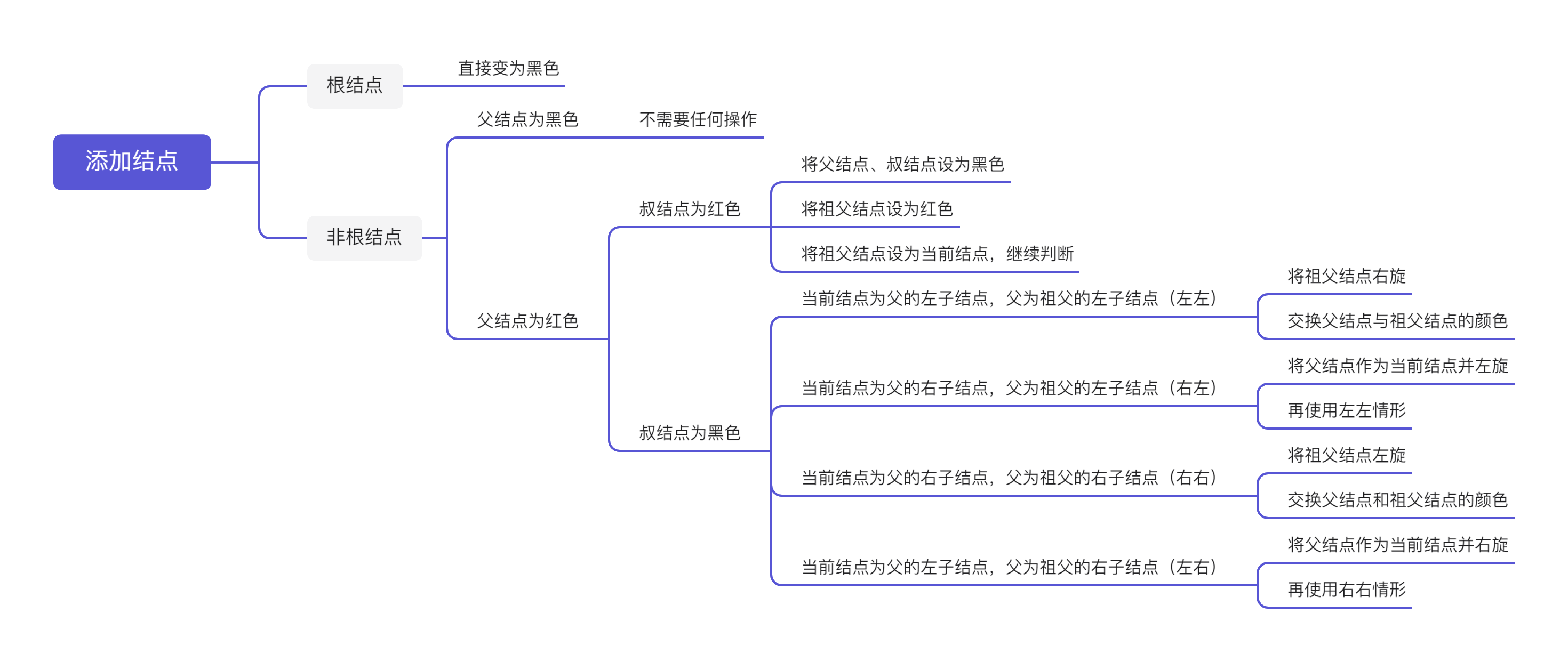
2-5.4 向红黑树中添加结点
按照红黑树的添加规则,现有一下数据准备添加到红黑树中:
将上述数据从左到右依次添加进红黑树中:
至此,上述数据添加完毕。
在上述数据的基础上,继续往红黑树中添加新数据:
至此,新数据添加完毕。
再次修改新数据,将新数据的最后一个更改为 16:




















 浙公网安备 33010602011771号
浙公网安备 33010602011771号