VS Code代码提示( AcWing算法模板,C++实现)
算法模板提取于AcWing上的代码提示
作者:yxc
链接:https://www.acwing.com/file_system/file/content/whole/index/content/2145234/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
已收录的模板及对应的唤醒词列表
vector<int> add add - 高精度加法
vector<int> sub sub - 高精度减法
vector<int> mul mul - 高精度乘低精度
vector<int> div div - 高精度除以低精度
int lo int lowbit - 找末尾1
void man void manacher - 马拉车算法 算法进阶课 ———— 第七章 基础算法
void mer void merge_sort - 归并排序
void bu void build - AC自动机 算法提高课 ———— 第四章 高级数据结构
int lo int lowbit - 树状数组 算法提高课 ———— 第四章 高级数据结构
bool dfs bool dfs - DLX重复覆盖 算法进阶课 ———— 第二章 数据结构
bool dfs bool dfs - DLX精确覆盖 算法进阶课 ———— 第二章 数据结构
int find int find - 并查集
int mer int merge - 左偏树 算法进阶课 ———— 第二章 数据结构
void spl void splay - 动态树 算法进阶课 ———— 第二章 数据结构
void bu void build - 线段树 算法提高课 ———— 第四章 高级数据结构
void spl void splay - splay 算法进阶课 ———— 第二章 数据结构
ULL get ULL get - 字符串哈希
void get_sa void get_sa - 后缀数组 算法进阶课 ———— 第二章 数据结构
void ext void extend - 后缀自动机 算法进阶课 ———— 第二章 数据结构
void ins void insert - Trie 插入
void ad void add - 加边,不带权
void ad void add - 加边,带权
void ad void add - 加边,最大流 算法进阶课 ———— 第一章 图论
void ad void add - 加边,费用流 算法进阶课 ———— 第一章 图论
void cost void cost_flow - 费用流 算法进阶课 ———— 第一章 图论
int cost int cost_flow - 费用流 算法进阶课 ———— 第一章 图论
int dij int dijkstra - 最短路
void dij void dijkstra - 最短路
int din int dinic - 最大流 算法进阶课 ———— 第一章 图论
void tar tarjan - e-无向图双连通分量 算法提高课 ———— 第三章 图论
bool find bool find - 匈牙利算法
int lca int lca - 倍增求LCA 算法提高课 ———— 第三章 图论
void tar tarjan - 有向图强连通分量 算法提高课 ———— 第三章 图论
int spf int spfa - 最短路
void spf void spfa - 最短路
bool spf bool spfa - 判负环
void top void topsort - 拓扑排序
bool top bool topsort - 拓扑排序
void tar tarjan - v-无向图双连通分量 算法提高课 ———— 第三章 图论
void andr void andrew - 求凸包 算法进阶课 ———— 第四章 计算几何
void hal half... - 求半平面交 算法进阶课 ———— 第四章 计算几何
int sig int sign - 计算几何常用函数 算法进阶课 ———— 第四章 计算几何
double sim double simpson - 辛普森积分 算法进阶课 ———— 第四章 计算几何
int bs int bsgs - BSGS 算法进阶课 ———— 第五章 数学
int phi int phi - 欧拉函数
void get_eu get_eulers - 线性筛欧拉函数
void ff void fft - FFT 算法进阶课 ———— 第五章 数学
int gau gauss - 高斯消元(浮点值)
void gau gauss - 高斯消元(浮点值)
int gau gauss - 高斯消元(布尔值)
void gau gauss - 高斯消元(布尔值)
int gc int gcd - 欧几里得算法
LL gc LL gcd - 欧几里得算法
int exgc int exgcd - 扩展欧几里得算法
int lu int lucas - Lucas定理
bool is_p bool is_prime - 判定质数
void get_p void get_primes - 线性筛质数
int qm int qmi - 快速幂
int qu int quick_power - 快速幂
void sim simulate_anneal - 模拟退火 算法进阶课 ———— 第六章 搜索
int h int h[N]...邻接表不带权
int h int h[N]...邻接表spfa
int h int h[N]...邻接表dijkstra
int h int h[N]...邻接表最大流 算法进阶课 ———— 第一章 图论
int h int h[N]...邻接表费用流 算法进阶课 ———— 第一章 图论
int h int h[N]...邻接表tarjan-scc 算法提高课 ———— 第三章 图论
int h int h[N]...邻接表tarjan-e-dcc 算法提高课 ———— 第三章 图论
int h int h[N]...邻接表tarjan-v-dcc 算法提高课 ———— 第三章 图论
VS Code配置,在设置中打开用户代码片段

在接下来的页面选择cpp.json
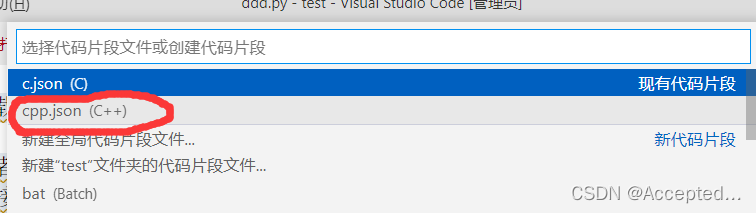
粘贴下面的代码,保存退出即可
{
"add - 高精度加法": {
"prefix": "vector<int> add",
"body": "vector<int> add(vector<int> &A, vector<int> &B) // C = A + B, A >= 0, B >= 0\n{\n if (A.size() < B.size()) return add(B, A);\n\n vector<int> C;\n int t = 0;\n for (int i = 0; i < A.size(); i ++ )\n {\n t += A[i];\n if (i < B.size()) t += B[i];\n C.push_back(t % 10);\n t /= 10;\n }\n\n if (t) C.push_back(t);\n return C;\n}\n",
"description": "vector<int> add - 高精度加法"
},
"sub - 高精度减法": {
"prefix": "vector<int> sub",
"body": "vector<int> sub(vector<int> &A, vector<int> &B) // C = A - B, 满足A >= B, A >= 0, B >= 0\n{\n vector<int> C;\n for (int i = 0, t = 0; i < A.size(); i ++ )\n {\n t = A[i] - t;\n if (i < B.size()) t -= B[i];\n C.push_back((t + 10) % 10);\n if (t < 0) t = 1;\n else t = 0;\n }\n\n while (C.size() > 1 && C.back() == 0) C.pop_back();\n return C;\n}\n",
"description": "vector<int> sub - 高精度减法"
},
"mul - 高精度乘低精度": {
"prefix": "vector<int> mul",
"body": "vector<int> mul(vector<int> &A, int b) // C = A * b, A >= 0, b >= 0\n{\n vector<int> C;\n\n int t = 0;\n for (int i = 0; i < A.size() || t; i ++ )\n {\n if (i < A.size()) t += A[i] * b;\n C.push_back(t % 10);\n t /= 10;\n }\n\n while (C.size() > 1 && C.back() == 0) C.pop_back();\n\n return C;\n}\n",
"description": "vector<int> mul - 高精度乘低精度"
},
"div - 高精度除以低精度": {
"prefix": "vector<int> div",
"body": "vector<int> div(vector<int> &A, int b, int &r) // A / b = C ... r, A >= 0, b > 0\n{\n vector<int> C;\n r = 0;\n for (int i = A.size() - 1; i >= 0; i -- )\n {\n r = r * 10 + A[i];\n C.push_back(r / b);\n r %= b;\n }\n reverse(C.begin(), C.end());\n while (C.size() > 1 && C.back() == 0) C.pop_back();\n return C;\n}\n",
"description": "vector<int> div - 高精度除以低精度"
},
"int lowbit - 找末尾1": {
"prefix": "int lowbit",
"body": "int lowbit(int x) // 返回末尾的1\n{\n return x & -x;\n}\n",
"description": "int lowbit - 找末尾1"
},
"void manacher - 马拉车算法": {
"prefix": "void manacher",
"body": "void init() // a[]为原串,b[]为插入'#'后的新串\n{\n int k = 0;\n b[k ++ ] = '$', b[k ++ ] = '#';\n for (int i = 0; i < n; i ++ ) b[k ++ ] = a[i], b[k ++ ] = '#';\n b[k ++ ] = '^';\n n = k;\n}\n\nvoid manacher() // 马拉车算法,b[]为插入'#'后的新串\n{\n int mr = 0, mid;\n for (int i = 1; i < n; i ++ )\n {\n if (i < mr) p[i] = min(p[mid * 2 - i], mr - i);\n else p[i] = 1;\n while (b[i - p[i]] == b[i + p[i]]) p[i] ++ ;\n if (i + p[i] > mr)\n {\n mr = i + p[i];\n mid = i;\n }\n }\n}\n",
"description": "void manacher - 马拉车算法"
},
"void merge_sort - 归并排序": {
"prefix": "void merge_sort",
"body": "void merge_sort(int q[], int l, int r) // 归并排序\n{\n if (l >= r) return;\n\n int mid = l + r >> 1;\n merge_sort(q, l, mid);\n merge_sort(q, mid + 1, r);\n\n int k = 0, i = l, j = mid + 1;\n while (i <= mid && j <= r)\n if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];\n else tmp[k ++ ] = q[j ++ ];\n\n while (i <= mid) tmp[k ++ ] = q[i ++ ];\n while (j <= r) tmp[k ++ ] = q[j ++ ];\n\n for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];\n}\n",
"description": "void merge_sort - 归并排序"
},
"void build - AC自动机": {
"prefix": "void build",
"body": "void insert(char str[]) // 将str插入Trie中\n{\n int p = 0;\n for (int i = 0; str[i]; i ++ )\n {\n int u = str[i] - 'a';\n if (!tr[p][u]) tr[p][u] = ++ idx;\n p = tr[p][u];\n }\n cnt[p] ++ ; // 记录单词出现次数\n}\n\nvoid build() // 创建AC自动机\n{\n int hh = 0, tt = -1;\n for (int i = 0; i < 26; i ++ )\n if (tr[0][i])\n q[ ++ tt] = tr[0][i];\n while (hh <= tt)\n {\n int t = q[hh ++ ];\n for (int i = 0; i < 26; i ++ )\n {\n int p = tr[t][i];\n if (!p) tr[t][i] = tr[ne[t]][i];\n else\n {\n ne[p] = tr[ne[t]][i];\n cnt[p] += cnt[ne[p]];\n q[ ++ tt] = p;\n }\n }\n }\n}\n",
"description": "void build - AC自动机"
},
"int lowbit - 树状数组": {
"prefix": "int lowbit",
"body": "lowbit(int x)\n{\n return x & -x;\n}\n\nvoid update(int x, int c) // 位置x加c\n{\n for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;\n}\n\nint query(int x) // 返回前x个数的和\n{\n int res = 0;\n for (int i = x; i; i -= lowbit(i)) res += tr[i];\n return res;\n}\n",
"description": "int lowbit - 树状数组"
},
"bool dfs - DLX重复覆盖": {
"prefix": "bool dfs",
"body": "int l[N], r[N], u[N], d[N], col[N], row[N], s[N], idx;\nint ans[N], top; // 记录选择了哪些行\nbool st[M]; // N为节点数,M为列数\n\nvoid init() // 初始化十字链表\n{\n for (int i = 0; i <= m; i ++ )\n {\n l[i] = i - 1, r[i] = i + 1;\n u[i] = d[i] = i;\n s[i] = 0, col[i] = i;\n }\n l[0] = m, r[m] = 0;\n idx = m + 1;\n}\n\nvoid add(int& hh, int& tt, int x, int y) // 在十字链表中插入节点\n{\n row[idx] = x, col[idx] = y, s[y] ++ ;\n u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;\n r[hh] = l[tt] = idx, r[idx] = tt, l[idx] = hh;\n tt = idx ++ ;\n}\n\nint h() // IDA*的启发函数\n{\n int res = 0;\n memset(st, 0, sizeof st);\n for (int i = r[0]; i; i = r[i])\n {\n if (st[col[i]]) continue;\n res ++ ;\n st[col[i]] = true;\n for (int j = d[i]; j != i; j = d[j])\n for (int k = r[j]; k != j; k = r[k])\n st[col[k]] = true;\n }\n return res;\n}\n\nvoid remove(int p)\n{\n for (int i = d[p]; i != p; i = d[i])\n {\n r[l[i]] = r[i];\n l[r[i]] = l[i];\n }\n}\n\nvoid resume(int p)\n{\n for (int i = u[p]; i != p; i = u[i])\n {\n r[l[i]] = i;\n l[r[i]] = i;\n }\n}\n\nbool dfs(int k)\n{\n if (k + h() > top) return false;\n if (!r[0])\n {\n top = k;\n return true;\n }\n int p = r[0];\n for (int i = r[0]; i; i = r[i])\n if (s[i] < s[p])\n p = i;\n for (int i = d[p]; i != p; i = d[i])\n {\n ans[k] = row[i];\n remove(i);\n for (int j = r[i]; j != i; j = r[j]) remove(j);\n if (dfs(k + 1)) return true;\n for (int j = l[i]; j != i; j = l[j]) resume(j);\n resume(i);\n }\n return false;\n}\n",
"description": "bool dfs - DLX重复覆盖"
},
"bool dfs - DLX精确覆盖": {
"prefix": "bool dfs",
"body": "int l[N], r[N], u[N], d[N], col[N], row[N], s[N], idx;\nint ans[N], top; // 记录选择了哪些行\n\nvoid init() // 初始化十字链表\n{\n for (int i = 0; i <= m; i ++ )\n {\n l[i] = i - 1, r[i] = i + 1;\n u[i] = d[i] = i;\n }\n l[0] = m, r[m] = 0;\n idx = m + 1;\n}\n\nvoid add(int& hh, int& tt, int x, int y) // 在十字链表中添加节点\n{\n row[idx] = x, col[idx] = y, s[y] ++ ;\n u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;\n r[hh] = l[tt] = idx, r[idx] = tt, l[idx] = hh;\n tt = idx ++ ;\n}\n\nvoid remove(int p)\n{\n r[l[p]] = r[p], l[r[p]] = l[p];\n for (int i = d[p]; i != p; i = d[i])\n for (int j = r[i]; j != i; j = r[j])\n {\n s[col[j]] -- ;\n d[u[j]] = d[j], u[d[j]] = u[j];\n }\n}\n\nvoid resume(int p)\n{\n for (int i = d[p]; i != p; i = d[i])\n for (int j = r[i]; j != i; j = r[j])\n {\n s[col[j]] ++ ;\n d[u[j]] = j, u[d[j]] = j;\n }\n r[l[p]] = p, l[r[p]] = p;\n}\n\nbool dfs()\n{\n if (!r[0]) return true;\n int p = r[0];\n for (int i = r[0]; i; i = r[i])\n if (s[i] < s[p])\n p = i;\n if (!s[p]) return false;\n remove(p);\n for (int i = d[p]; i != p; i = d[i])\n {\n ans[ ++ top] = row[i];\n for (int j = r[i]; j != i; j = r[j]) remove(col[j]);\n if (dfs()) return true;\n for (int j = r[i]; j != i; j = r[j]) resume(col[j]);\n top -- ;\n }\n resume(p);\n return false;\n}\n",
"description": "bool dfs - DLX精确覆盖"
},
"int find - 并查集": {
"prefix": "int find",
"body": "int find(int x) // 并查集\n{\n if (p[x] != x) p[x] = find(p[x]);\n return p[x];\n}\n",
"description": "int find - 并查集"
},
"int merge - 左偏树": {
"prefix": "int merge",
"body": "int v[N], dist[N], l[N], r[N], idx;\n\nbool cmp(int x, int y) // 比较两个节点的权值大小\n{\n if (v[x] != v[y]) return v[x] < v[y];\n return x < y;\n}\n\nint merge(int x, int y) // 合并两棵左偏树\n{\n if (!x || !y) return x + y;\n if (cmp(y, x)) swap(x, y);\n r[x] = merge(r[x], y);\n if (dist[r[x]] > dist[l[x]]) swap(l[x], r[x]);\n dist[x] = dist[r[x]] + 1;\n return x;\n}\n",
"description": "int merge - 左偏树"
},
"void splay - 动态树": {
"prefix": "void splay",
"body": "struct Node\n{\n int s[2], p, v;\n int rev;\n // TODO: 定义需要维护的信息和懒标记\n}tr[N];\nint stk[N]; // 栈\n\nvoid pushrev(int x)\n{\n swap(tr[x].s[0], tr[x].s[1]);\n tr[x].rev ^= 1;\n}\n\nvoid pushup(int x)\n{\n // TODO: 利用子节点信息来维护当前节点的信息\n}\n\nvoid pushdown(int x)\n{\n if (tr[x].rev)\n {\n pushrev(tr[x].s[0]), pushrev(tr[x].s[1]);\n tr[x].rev = 0;\n }\n // TODO: 将当前节点的懒标记下传\n}\n\nbool isroot(int x) // 判断x是否为原树的根节点\n{\n return tr[tr[x].p].s[0] != x && tr[tr[x].p].s[1] != x;\n}\n\nvoid rotate(int x) // splay的旋转操作\n{\n int y = tr[x].p, z = tr[y].p;\n int k = tr[y].s[1] == x;\n if (!isroot(y)) tr[z].s[tr[z].s[1] == y] = x;\n tr[x].p = z;\n tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;\n tr[x].s[k ^ 1] = y, tr[y].p = x;\n pushup(y), pushup(x);\n}\n\nvoid splay(int x) // splay操作\n{\n int top = 0, r = x;\n stk[ ++ top] = r;\n while (!isroot(r)) stk[ ++ top] = r = tr[r].p;\n while (top) pushdown(stk[top -- ]);\n while (!isroot(x))\n {\n int y = tr[x].p, z = tr[y].p;\n if (!isroot(y))\n if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);\n else rotate(y);\n rotate(x);\n }\n}\n\nvoid access(int x) // 建立一条从根到x的路径,同时将x变成splay的根节点\n{\n int z = x;\n for (int y = 0; x; y = x, x = tr[x].p)\n {\n splay(x);\n tr[x].s[1] = y, pushup(x);\n }\n splay(z);\n}\n\nvoid makeroot(int x) // 将x变成原树的根节点\n{\n access(x);\n pushrev(x);\n}\n\nint findroot(int x) // 找到x所在原树的根节点, 再将原树的根节点旋转到splay的根节点\n{\n access(x);\n while (tr[x].s[0]) pushdown(x), x = tr[x].s[0];\n splay(x);\n return x;\n}\n\nvoid split(int x, int y) // 给x和y之间的路径建立一个splay,其根节点是y\n{\n makeroot(x);\n access(y);\n}\n\nvoid link(int x, int y) // 如果x和y不连通,则加入一条x和y之间的边\n{\n makeroot(x);\n if (findroot(y) != x) tr[x].p = y;\n}\n\nvoid cut(int x, int y) // 如果x和y之间存在边,则删除该边\n{\n makeroot(x);\n if (findroot(y) == x && tr[y].p == x && !tr[y].s[0])\n {\n tr[x].s[1] = tr[y].p = 0;\n pushup(x);\n }\n}\n",
"description": "void splay - 动态树"
},
"void build - 线段树": {
"prefix": "void build",
"body": "struct Node\n{\n int l, r;\n // TODO: 需要维护的信息和懒标记\n}tr[N * 4];\n\nvoid pushup(int u)\n{\n // TODO: 利用左右儿子信息维护当前节点的信息\n}\n\nvoid pushdown(int u)\n{\n // TODO: 将懒标记下传\n}\n\nvoid build(int u, int l, int r)\n{\n if (l == r) tr[u] = {l, r};\n else\n {\n tr[u] = {l, r};\n int mid = l + r >> 1;\n build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);\n pushup(u);\n }\n}\n\nvoid update(int u, int l, int r, int d)\n{\n if (tr[u].l >= l && tr[u].r <= r)\n {\n // TODO: 修改区间\n }\n else\n {\n pushdown(u);\n int mid = tr[u].l + tr[u].r >> 1;\n if (l <= mid) update(u << 1, l, r, d);\n if (r > mid) update(u << 1 | 1, l, r, d);\n pushup(u);\n }\n}\n\nint query(int u, int l, int r)\n{\n if (tr[u].l >= l && tr[u].r <= r)\n {\n return ; // TODO 需要补充返回值\n }\n else\n {\n pushdown(u);\n int mid = tr[u].l + tr[u].r >> 1;\n int res = 0;\n if (l <= mid ) res = query(u << 1, l, r);\n if (r > mid) res += query(u << 1 | 1, l, r);\n return res;\n }\n}\n",
"description": "void build - 线段树"
},
"void splay - splay": {
"prefix": "void splay",
"body": "struct Node\n{\n int s[2], p, v;\n int size;\n \n void init(int _v, int _p)\n {\n v = _v, p = _p;\n size = 1;\n }\n}tr[N];\nint root, idx;\n\nvoid pushup(int x)\n{\n // TODO: 利用子节点信息维护当前节点信息\n}\n\nvoid pushdown(int x)\n{\n // TODO: 将懒标记下传\n}\n\nvoid rotate(int x) // 旋转\n{\n int y = tr[x].p, z = tr[y].p;\n int k = tr[y].s[1] == x;\n tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;\n tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;\n tr[x].s[k ^ 1] = y, tr[y].p = x;\n pushup(y), pushup(x);\n}\n\nvoid splay(int x, int k) // splay操作\n{\n while (tr[x].p != k)\n {\n int y = tr[x].p, z = tr[y].p;\n if (z != k)\n if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);\n else rotate(y);\n rotate(x);\n }\n if (!k) root = x;\n}\n",
"description": "void splay - splay"
},
"ULL get - 字符串哈希": {
"prefix": "ULL get",
"body": "ULL get(int l, int r) // 计算子串 str[l ~ r] 的哈希值\n{\n return h[r] - h[l - 1] * p[r - l + 1];\n}\n",
"description": "ULL get - 字符串哈希"
},
"void get_sa - 后缀数组": {
"prefix": "void get_sa",
"body": "char s[N]; // 存储原字符串\nint sa[N], rk[N], x[N], y[N], height[N], c[N];\n\nvoid get_sa() // 创建后缀数组\n{\n for (int i = 1; i <= n; i ++ ) c[x[i] = s[i]] ++ ;\n for (int i = 2; i <= m; i ++ ) c[i] += c[i - 1];\n for (int i = n; i; i -- ) sa[c[x[i]] -- ] = i;\n for (int k = 1; k <= n; k <<= 1)\n {\n int num = 0;\n for (int i = n - k + 1; i <= n; i ++ ) y[ ++ num] = i;\n for (int i = 1; i <= n; i ++ )\n if (sa[i] > k)\n y[ ++ num] = sa[i] - k;\n for (int i = 1; i <= m; i ++ ) c[i] = 0;\n for (int i = 1; i <= n; i ++ ) c[x[i]] ++ ;\n for (int i = 2; i <= m; i ++ ) c[i] += c[i - 1];\n for (int i = n; i; i -- ) sa[c[x[y[i]]] -- ] = y[i], y[i] = 0;\n swap(x, y);\n x[sa[1]] = 1, num = 1;\n for (int i = 2; i <= n; i ++ )\n x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++ num;\n if (num == n) break;\n m = num;\n }\n}\n\nvoid get_height() // 预处理height[]数组\n{\n int k = 0;\n for (int i = 1; i <= n; i ++ ) rk[sa[i]] = i;\n for (int i = 1; i <= n; i ++ )\n {\n if (rk[i] == 1) continue;\n if (k) k -- ;\n int j = sa[rk[i] - 1];\n while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k ++ ;\n height[rk[i]] = k;\n }\n}\n",
"description": "void get_sa - 后缀数组"
},
"void extend - 后缀自动机": {
"prefix": "void extend",
"body": "int tot = 1, last = 1;\nstruct Node\n{\n int len, fa;\n int ch[26];\n}node[N];\n\nvoid extend(char c)\n{\n int p = last, np = last = ++ tot;\n node[np].len = node[p].len + 1;\n for (; p && !node[p].ch[c]; p = node[p].fa) node[p].ch[c] = np;\n if (!p) node[np].fa = 1;\n else\n {\n int q = node[p].ch[c];\n if (node[q].len == node[p].len + 1) node[np].fa = q;\n else\n {\n int nq = ++ tot;\n node[nq] = node[q], node[nq].len = node[p].len + 1;\n node[q].fa = node[np].fa = nq;\n for (; p && node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;\n }\n }\n}\n",
"description": "void extend - 后缀自动机"
},
"void insert - Trie 插入": {
"prefix": "void insert",
"body": "int son[N][26], cnt[N], idx;\n\nvoid insert(char *str) // 插入字符串\n{\n int p = 0;\n for (int i = 0; str[i]; i ++ )\n {\n int u = str[i] - 'a';\n if (!son[p][u]) son[p][u] = ++ idx;\n p = son[p][u];\n }\n cnt[p] ++ ;\n}\n\nint query(char *str) // 查询字符串出现次数\n{\n int p = 0;\n for (int i = 0; str[i]; i ++ )\n {\n int u = str[i] - 'a';\n if (!son[p][u]) return 0;\n p = son[p][u];\n }\n return cnt[p];\n}\n",
"description": "void insert - Trie 插入"
},
"void add - 加边,不带权": {
"prefix": "void add",
"body": "void add(int a, int b) // 添加一条边a->b\n{\n e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;\n}\n",
"description": "void add - 加边,不带权"
},
"void add - 加边,带权": {
"prefix": "void add",
"body": "void add(int a, int b, int c) // 添加一条边a->b,边权为c\n{\n e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;\n}\n",
"description": "void add - 加边,带权"
},
"void add - 加边,最大流": {
"prefix": "void add",
"body": "void add(int a, int b, int c) // 添加一条边a->b,容量为c;同时添加一条反向边\n{\n e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;\n e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx ++ ;\n}\n",
"description": "void add - 加边,最大流"
},
"void add - 加边,费用流": {
"prefix": "void add",
"body": "void add(int a, int b, int c, int d) // 添加一条边a->b,容量为c,费用为d;同时增加一条反向边\n{\n e[idx] = b, f[idx] = c, w[idx] = d, ne[idx] = h[a], h[a] = idx ++ ;\n e[idx] = a, f[idx] = 0, w[idx] = -d, ne[idx] = h[b], h[b] = idx ++ ;\n}\n",
"description": "void add - 加边,费用流"
},
"void cost_flow - 费用流": {
"prefix": "void cost",
"body": "bool spfa() // 找距离最短的增广路\n{\n int hh = 0, tt = 1;\n memset(d, 0x3f, sizeof d);\n q[0] = S, d[S] = 0, incf[S] = INF;\n while (hh != tt)\n {\n int t = q[hh ++ ];\n if (hh == N) hh = 0;\n st[t] = false;\n for (int i = h[t]; ~i; i = ne[i])\n {\n int ver = e[i];\n if (f[i] && d[ver] > d[t] + w[i])\n {\n d[ver] = d[t] + w[i];\n pre[ver] = i;\n incf[ver] = min(f[i], incf[t]);\n if (!st[ver])\n {\n q[tt ++ ] = ver;\n if (tt == N) tt = 0;\n st[ver] = true;\n }\n }\n }\n }\n return d[T] != INF;\n}\n\nvoid cost_flow(int& flow, int& cost)\n{\n flow = cost = 0; // flow存储流量,cost存储费用\n while (spfa())\n {\n int t = incf[T];\n flow += t, cost += t * d[T];\n for (int i = T; i != S; i = e[pre[i] ^ 1])\n {\n f[pre[i]] -= t;\n f[pre[i] ^ 1] += t;\n }\n }\n}\n",
"description": "void cost_flow - 费用流"
},
"int cost_flow - 费用流": {
"prefix": "int cost",
"body": "bool spfa() // 找距离最短的增广路\n{\n int hh = 0, tt = 1;\n memset(d, 0x3f, sizeof d);\n q[0] = S, d[S] = 0, incf[S] = INF;\n while (hh != tt)\n {\n int t = q[hh ++ ];\n if (hh == N) hh = 0;\n st[t] = false;\n for (int i = h[t]; ~i; i = ne[i])\n {\n int ver = e[i];\n if (f[i] && d[ver] > d[t] + w[i])\n {\n d[ver] = d[t] + w[i];\n pre[ver] = i;\n incf[ver] = min(f[i], incf[t]);\n if (!st[ver])\n {\n q[tt ++ ] = ver;\n if (tt == N) tt = 0;\n st[ver] = true;\n }\n }\n }\n }\n return d[T] != INF;\n}\n\nint cost_flow()\n{\n int cost = 0; // 存储费用\n while (spfa())\n {\n int t = incf[T];\n cost += t * d[T];\n for (int i = T; i != S; i = e[pre[i] ^ 1])\n {\n f[pre[i]] -= t;\n f[pre[i] ^ 1] += t;\n }\n }\n return cost;\n}\n",
"description": "int cost_flow - 费用流"
},
"int dijkstra - 最短路": {
"prefix": "int dijkstra",
"body": "int dijkstra() // 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1\n{\n memset(dist, 0x3f, sizeof dist);\n dist[1] = 0;\n priority_queue<PII, vector<PII>, greater<PII>> heap;\n heap.push({0, 1});\n\n while (heap.size())\n {\n auto t = heap.top();\n heap.pop();\n\n int ver = t.second, distance = t.first;\n\n if (st[ver]) continue;\n st[ver] = true;\n\n for (int i = h[ver]; i != -1; i = ne[i])\n {\n int j = e[i];\n if (dist[j] > dist[ver] + w[i])\n {\n dist[j] = dist[ver] + w[i];\n heap.push({dist[j], j});\n }\n }\n }\n\n if (dist[n] == 0x3f3f3f3f) return -1;\n return dist[n];\n}\n",
"description": "int dijkstra - 最短路"
},
"void dijkstra - 最短路": {
"prefix": "void dijkstra",
"body": "void dijkstra() // 求1号点到n号点的最短路距离\n{\n memset(dist, 0x3f, sizeof dist);\n dist[1] = 0;\n priority_queue<PII, vector<PII>, greater<PII>> heap;\n heap.push({0, 1});\n\n while (heap.size())\n {\n auto t = heap.top();\n heap.pop();\n\n int ver = t.second, distance = t.first;\n\n if (st[ver]) continue;\n st[ver] = true;\n\n for (int i = h[ver]; i != -1; i = ne[i])\n {\n int j = e[i];\n if (dist[j] > dist[ver] + w[i])\n {\n dist[j] = dist[ver] + w[i];\n heap.push({dist[j], j});\n }\n }\n }\n}\n",
"description": "void dijkstra - 最短路"
},
"int dinic - 最大流": {
"prefix": "int din",
"body": "bool bfs() // 创建分层图\n{\n int hh = 0, tt = 0;\n memset(d, -1, sizeof d);\n q[0] = S, d[S] = 0, cur[S] = h[S];\n while (hh <= tt)\n {\n int t = q[hh ++ ];\n for (int i = h[t]; ~i; i = ne[i])\n {\n int ver = e[i];\n if (d[ver] == -1 && f[i])\n {\n d[ver] = d[t] + 1;\n cur[ver] = h[ver];\n if (ver == T) return true;\n q[ ++ tt] = ver;\n }\n }\n }\n return false; // 没有增广路\n}\n\nint find(int u, int limit) // 在残留网络中增广\n{\n if (u == T) return limit;\n int flow = 0;\n for (int i = cur[u]; ~i && flow < limit; i = ne[i])\n {\n cur[u] = i; // 当前弧优化\n int ver = e[i];\n if (d[ver] == d[u] + 1 && f[i])\n {\n int t = find(ver, min(f[i], limit - flow));\n if (!t) d[ver] = -1;\n f[i] -= t, f[i ^ 1] += t, flow += t;\n }\n }\n return flow;\n}\n\nint dinic()\n{\n int r = 0, flow;\n while (bfs()) while (flow = find(S, INF)) r += flow;\n return r;\n}\n",
"description": "int dinic - 最大流"
},
"tarjan - e-无向图双连通分量": {
"prefix": "void tarjan",
"body": "void tarjan(int u, int from)\n{\n dfn[u] = low[u] = ++ timestamp;\n stk[ ++ top] = u;\n \n for (int i = h[u]; ~i; i = ne[i])\n {\n int j = e[i];\n if (!dfn[j])\n {\n tarjan(j, i);\n low[u] = min(low[u], low[j]);\n if (dfn[u] < low[j])\n is_bridge[i] = is_bridge[i ^ 1] = true;\n }\n else if (i != (from ^ 1))\n low[u] = min(low[u], dfn[j]);\n }\n \n if (dfn[u] == low[u])\n {\n ++ dcc_cnt;\n int y;\n do {\n y = stk[top -- ];\n id[y] = dcc_cnt;\n } while (y != u);\n }\n}\n",
"description": "void tarjan - e-无向图双连通分量"
},
"bool find - 匈牙利算法": {
"prefix": "bool find",
"body": "bool find(int x)\n{\n for (int i = h[x]; i != -1; i = ne[i])\n {\n int j = e[i];\n if (!st[j])\n {\n st[j] = true;\n if (match[j] == 0 || find(match[j]))\n {\n match[j] = x;\n return true;\n }\n }\n }\n \n return false;\n}\n",
"description": "bool find - 匈牙利算法"
},
"int lca - 倍增求LCA": {
"prefix": "int lca",
"body": "void bfs(int root) // 预处理倍增数组\n{\n memset(depth, 0x3f, sizeof depth);\n depth[0] = 0, depth[root] = 1; // depth存储节点所在层数\n int hh = 0, tt = 0;\n q[0] = root;\n while (hh <= tt)\n {\n int t = q[hh ++ ];\n for (int i = h[t]; ~i; i = ne[i])\n {\n int j = e[i];\n if (depth[j] > depth[t] + 1)\n {\n depth[j] = depth[t] + 1;\n q[ ++ tt] = j;\n fa[j][0] = t; // j的第二次幂个父节点\n for (int k = 1; k <= 15; k ++ )\n fa[j][k] = fa[fa[j][k - 1]][k - 1];\n }\n }\n }\n}\n\nint lca(int a, int b) // 返回a和b的最近公共祖先\n{\n if (depth[a] < depth[b]) swap(a, b);\n for (int k = 15; k >= 0; k -- )\n if (depth[fa[a][k]] >= depth[b])\n a = fa[a][k];\n if (a == b) return a;\n for (int k = 15; k >= 0; k -- )\n if (fa[a][k] != fa[b][k])\n {\n a = fa[a][k];\n b = fa[b][k];\n }\n return fa[a][0];\n}\n",
"description": "int lca - 倍增求LCA"
},
"tarjan - 有向图强连通分量": {
"prefix": "void tarjan",
"body": "void tarjan(int u)\n{\n dfn[u] = low[u] = ++ timestamp;\n stk[ ++ top] = u, in_stk[u] = true;\n \n for (int i = h[u]; ~i; i = ne[i])\n {\n int j = e[i];\n if (!dfn[j])\n {\n tarjan(j);\n low[u] = min(low[u], low[j]);\n }\n else if (in_stk[j])\n low[u] = min(low[u], dfn[j]);\n }\n \n if (dfn[u] == low[u])\n {\n ++ scc_cnt;\n int y;\n do {\n y = stk[top -- ];\n in_stk[y] = false;\n id[y] = scc_cnt;\n } while (y != u);\n }\n}\n",
"description": "void tarjan - 有向图强连通分量"
},
"int spfa - 最短路": {
"prefix": "int spf",
"body": "int spfa() // 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1\n{\n int hh = 0, tt = 0;\n memset(dist, 0x3f, sizeof dist);\n dist[1] = 0;\n q[tt ++ ] = 1;\n st[1] = true;\n\n while (hh != tt)\n {\n int t = q[hh ++ ];\n if (hh == N) hh = 0;\n st[t] = false;\n \n for (int i = h[t]; i != -1; i = ne[i])\n {\n int j = e[i];\n if (dist[j] > dist[t] + w[i])\n {\n dist[j] = dist[t] + w[i];\n if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入\n {\n q[tt ++ ] = j;\n if (tt == N) tt = 0;\n st[j] = true;\n }\n }\n }\n }\n\n if (dist[n] == 0x3f3f3f3f) return -1;\n return dist[n];\n}\n",
"description": "int spfa - 最短路"
},
"void spfa - 最短路": {
"prefix": "void spfa",
"body": "void spfa() // 求1号点到n号点的最短路距离\n{\n int hh = 0, tt = 0;\n memset(dist, 0x3f, sizeof dist);\n dist[1] = 0;\n q[tt ++ ] = 1;\n st[1] = true;\n\n while (hh != tt)\n {\n int t = q[hh ++ ];\n if (hh == N) hh = 0;\n st[t] = false;\n \n for (int i = h[t]; i != -1; i = ne[i])\n {\n int j = e[i];\n if (dist[j] > dist[t] + w[i])\n {\n dist[j] = dist[t] + w[i];\n if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入\n {\n q[tt ++ ] = j;\n if (tt == N) tt = 0;\n st[j] = true;\n }\n }\n }\n }\n}\n",
"description": "void spfa - 最短路"
},
"bool spfa - 判负环": {
"prefix": "bool spfa",
"body": "bool spfa() // 如果存在负环,则返回true,否则返回false。\n{\n // 不需要初始化dist数组\n // 原理:如果某条最短路径上有n个点(除了自己),那么加上自己之后一共有n+1个点,\n // 由抽屉原理一定有两个点相同,所以存在环。\n\n int hh = 0, tt = 0;\n \n for (int i = 1; i <= n; i ++ ) q[tt ++ ] = i, st[i] = true;\n \n while (hh != tt)\n {\n int t = q[hh ++ ];\n if (hh == N) hh = 0;\n st[t] = false;\n \n for (int i = h[t]; ~i; i = ne[i])\n {\n int j = e[i];\n if (dist[j] > dist[t] + w[i])\n {\n dist[j] = dist[t] + w[i];\n cnt[j] = cnt[t] + 1;\n if (cnt[j] >= n) return true;\n if (!st[j])\n {\n st[j] = true;\n q[tt ++ ] = j;\n if (tt == N) tt = 0;\n }\n }\n }\n }\n \n return false;\n}\n",
"description": "bool spfa - 判负环"
},
"void topsort - 拓扑排序": {
"prefix": "void topsort",
"body": "void topsort()\n{\n int hh = 0, tt = -1;\n\n // d[i] 存储点i的入度\n for (int i = 1; i <= n; i ++ )\n if (!d[i])\n q[ ++ tt] = i;\n\n while (hh <= tt)\n {\n int t = q[hh ++ ];\n\n for (int i = h[t]; i != -1; i = ne[i])\n {\n int j = e[i];\n if (-- d[j] == 0)\n q[ ++ tt] = j;\n }\n }\n}\n",
"description": "void topsort - 拓扑排序"
},
"bool topsort - 拓扑排序": {
"prefix": "bool topsort",
"body": "bool topsort()\n{\n int hh = 0, tt = -1;\n\n // d[i] 存储点i的入度\n for (int i = 1; i <= n; i ++ )\n if (!d[i])\n q[ ++ tt] = i;\n\n while (hh <= tt)\n {\n int t = q[hh ++ ];\n\n for (int i = h[t]; i != -1; i = ne[i])\n {\n int j = e[i];\n if (-- d[j] == 0)\n q[ ++ tt] = j;\n }\n }\n\n // 如果所有点都入队了,说明存在拓扑序列;否则不存在拓扑序列。\n return tt == n - 1;\n}\n",
"description": "bool topsort - 拓扑排序"
},
"tarjan - v-无向图双连通分量": {
"prefix": "void tarjan",
"body": "void tarjan(int u)\n{\n dfn[u] = low[u] = ++ timestamp;\n stk[ ++ top] = u;\n \n if (u == root && h[u] == -1)\n {\n dcc_cnt ++ ;\n dcc[dcc_cnt].push_back(u);\n return;\n }\n \n int cnt = 0;\n for (int i = h[u]; ~i; i = ne[i])\n {\n int j = e[i];\n if (!dfn[j])\n {\n tarjan(j);\n low[u] = min(low[u], low[j]);\n if (dfn[u] <= low[j])\n {\n cnt ++ ;\n if (u != root || cnt > 1) cut[u] = true;\n ++ dcc_cnt;\n int y;\n do {\n y = stk[top -- ];\n dcc[dcc_cnt].push_back(y);\n } while (y != j);\n dcc[dcc_cnt].push_back(u);\n }\n }\n else low[u] = min(low[u], dfn[j]);\n }\n}\n",
"description": "void tarjan - v-无向图双连通分量"
},
"int bsgs - BSGS": {
"prefix": "int bsgs",
"body": "bsgs(int a, int b, int p) // a ^ x ≡ b (mod p) 的最小非负整数解\n{\n if (b == 1) return 0;\n int k = sqrt(p) + 1;\n unordered_map<int, int> hash;\n for (int i = 0, j = b; i < k; i ++ )\n {\n hash[j] = i;\n j = (LL)j * a % p;\n }\n int ak = 1;\n for (int i = 0; i < k; i ++ ) ak = (LL)ak * a % p;\n for (int i = 1, j = ak; i <= k; i ++ )\n {\n if (hash.count(j) && (LL)i * k >= hash[j])\n return (LL)i * k - hash[j];\n j = (LL)j * ak % p;\n }\n return -1;\n}\n",
"description": "int bsgs - BSGS"
},
"void andrew - 求凸包": {
"prefix": "void andr",
"body": "int stk[N], top;\nPDD q[N];\nbool used[N];\n\nPDD operator- (PDD a, PDD b) // 向量减法\n{\n return {a.x - b.x, a.y - b.y};\n}\n\ndouble operator* (PDD a, PDD b) // 叉积、外积\n{\n return a.x * b.y - a.y * b.x;\n}\n\ndouble operator& (PDD a, PDD b) // 内积、点积\n{\n return a.x * b.x + a.y * b.y;\n}\n\ndouble area(PDD a, PDD b, PDD c) // 以a, b, c为顶点的有向三角形面积\n{\n return (b - a) * (c - a);\n}\n\ndouble get_len(PDD a) // 求向量长度\n{\n return sqrt(a & a);\n}\n\ndouble get_dist(PDD a, PDD b) // 求两个点之间的距离\n{\n return get_len(b - a);\n}\n\nvoid andrew() // Andrew算法, 凸包节点编号逆时针存于stk中,下标从0开始\n{\n sort(q, q + n);\n for (int i = 0; i < n; i ++ )\n {\n while (top >= 2 && area(q[stk[top - 2]], q[stk[top - 1]], q[i]) <= 0)\n {\n if (area(q[stk[top - 2]], q[stk[top - 1]], q[i]) < 0)\n used[stk[ -- top]] = false;\n else\n top -- ;\n }\n stk[top ++ ] = i;\n used[i] = true;\n }\n used[0] = false;\n for (int i = n - 1; i >= 0; i -- )\n {\n if (used[i]) continue;\n while (top >= 2 && area(q[stk[top - 2]], q[stk[top - 1]], q[i]) <= 0)\n top -- ;\n stk[top ++ ] = i;\n }\n top -- ; // 起点重复添加了一次,将其去掉\n}\n",
"description": "void andrew - 求凸包"
},
"half... - 求半平面交": {
"prefix": "void hal",
"body": "struct Line // 直线\n{\n PDD st, ed; // 直线上的两个点\n}line[N];\nint q[N]; // 双端队列\n\nint sign(double x) // 符号函数\n{\n if (fabs(x) < eps) return 0; // x为0,则返回0\n if (x < 0) return -1; // x为负数,则返回-1\n return 1; // x为正数,则返回1\n}\n\nint dcmp(double x, double y) // 比较两数大小\n{\n if (fabs(x - y) < eps) return 0; // x == y, 返回0\n if (x < y) return -1; // x < y, 返回-1\n return 1; // x > y, 返回1\n}\n\nPDD operator+ (PDD a, PDD b) // 向量加法\n{\n return {a.x + b.x, a.y + b.y};\n}\n\nPDD operator-(PDD a, PDD b) // 向量减法\n{\n return {a.x - b.x, a.y - b.y};\n}\n\ndouble operator* (PDD a, PDD b) // 外积、叉积\n{\n return a.x * b.y - a.y * b.x;\n}\n\nPDD operator* (PDD a, double t) // 向量数乘\n{\n return {a.x * t, a.y * t};\n}\n\ndouble area(PDD a, PDD b, PDD c) // 以a, b, c为顶点的有向三角形面积\n{\n return (b - a) * (c - a);\n}\n\nPDD get_line_intersection(PDD p, PDD v, PDD q, PDD w) // 求两直线交点:p + vt, q + wt\n{\n auto u = p - q;\n auto t = w * u / (v * w);\n return p + v * t;\n}\n\nPDD get_line_intersection(Line a, Line b) // 求两直线交点\n{\n return get_line_intersection(a.st, a.ed - a.st, b.st, b.ed - b.st);\n}\n\nbool on_right(Line& a, Line& b, Line& c) // bc的交点是否在a的右侧\n{\n auto o = get_line_intersection(b, c);\n return sign(area(a.st, a.ed, o)) <= 0;\n}\n\ndouble get_angle(const Line& a) // 求直线的极角大小\n{\n return atan2(a.ed.y - a.st.y, a.ed.x - a.st.x);\n}\n\nbool cmp(const Line& a, const Line& b) // 将所有直线按极角排序\n{\n double A = get_angle(a), B = get_angle(b);\n if (!dcmp(A, B)) return area(a.st, a.ed, b.ed) < 0;\n return A < B;\n}\n\nvoid half_plane_intersection() // 半平面交,交集的边逆时针顺序存于q[]中\n{\n sort(line, line + cnt, cmp);\n int hh = 0, tt = -1;\n for (int i = 0; i < cnt; i ++ )\n {\n if (i && !dcmp(get_angle(line[i]), get_angle(line[i - 1]))) continue;\n while (hh + 1 <= tt && on_right(line[i], line[q[tt - 1]], line[q[tt]])) tt -- ;\n while (hh + 1 <= tt && on_right(line[i], line[q[hh]], line[q[hh + 1]])) hh ++ ;\n q[ ++ tt] = i;\n }\n while (hh + 1 <= tt && on_right(line[q[hh]], line[q[tt - 1]], line[q[tt]])) tt -- ;\n while (hh + 1 <= tt && on_right(line[q[tt]], line[q[hh]], line[q[hh + 1]])) hh ++ ;\n \n q[ ++ tt] = q[hh];\n // 交集的边逆时针顺序存于q[]中\n \n // TODO: 求出半平面交后,根据题目要求求答案\n}\n",
"description": "half... - 求半平面交"
},
"int sign - 计算几何常用函数": {
"prefix": "int sig",
"body": "int sig(double x) // 符号函数\n{\n if (fabs(x) < eps) return 0; // x为0,则返回0\n if (x < 0) return -1; // x为负数,则返回-1\n return 1; // x为正数,则返回1\n}\n\nint dcmp(double x, double y) // 比较两数大小\n{\n if (fabs(x - y) < eps) return 0; // x == y, 返回0\n if (x < y) return -1; // x < y, 返回-1\n return 1; // x > y, 返回1\n}\n\nPDD operator+ (PDD a, PDD b) // 向量加法\n{\n return {a.x + b.x, a.y + b.y};\n}\n\nPDD operator- (PDD a, PDD b) // 向量减法\n{\n return {a.x - b.x, a.y - b.y};\n}\n\nPDD operator* (PDD a, double t) // 向量数乘\n{\n return {a.x * t, a.y * t};\n}\n\nPDD operator/ (PDD a, double t) // 向量除以常数\n{\n return {a.x / t, a.y / t};\n}\n\ndouble operator* (PDD a, PDD b) // 外积、叉积\n{\n return a.x * b.y - a.y * b.x;\n}\n\ndouble operator& (PDD a, PDD b) // 内积、点积\n{\n return a.x * b.x + a.y * b.y;\n}\n\ndouble area(PDD a, PDD b, PDD c) // 以a, b, c为顶点的有向三角形面积\n{\n return (b - a) * (c - a);\n}\n\ndouble get_len(PDD a) // 求向量长度\n{\n return sqrt(a & a);\n}\n\ndouble get_dist(PDD a, PDD b) // 求两个点之间的距离\n{\n return get_len(b - a);\n}\n\ndouble project(PDD a, PDD b, PDD c) // 求向量ac在向量ab上的投影\n{\n return ((c - a) & (b - a)) / get_len(b - a);\n}\n\nPDD rotate(PDD a, double b) // 向量a逆时针旋转角度b\n{\n return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};\n}\n\nPDD norm(PDD a) // 矩阵标准化(将长度变成1)\n{\n return a / get_len(a);\n}\n\nbool on_segment(PDD p, PDD a, PDD b) // 点p是否在线段ab上(包含端点a、b)\n{\n return !sign((p - a) * (p - b)) && sign((p - a) & (p - b)) <= 0;\n}\n\nPDD get_line_intersection(PDD p, PDD v, PDD q, PDD w) // 求两直线交点:p + vt, q + wt\n{\n auto u = p - q;\n auto t = w * u / (v * w);\n return p + v * t;\n}\n",
"description": "int sign - 计算几何常用函数"
},
"double simpson - 辛普森积分": {
"prefix": "double sim",
"body": "double f(double x)\n{\n // TODO: 实现所求的函数\n}\n\ndouble simpson(double l, double r) // 辛普森积分公式\n{\n auto mid = (l + r) / 2;\n return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;\n}\n\ndouble asr(double l, double r, double s) // 自适应\n{\n auto mid = (l + r) / 2;\n auto left = simpson(l, mid), right = simpson(mid, r);\n if (fabs(left + right - s) < eps) return left + right;\n return asr(l, mid, left) + asr(mid, r, right);\n}\n",
"description": "double simpson - 辛普森积分"
},
"int phi - 欧拉函数": {
"prefix": "int phi",
"body": "int phi(int x) // 欧拉函数\n{\n int res = x;\n for (int i = 2; i <= x / i; i ++ )\n if (x % i == 0)\n {\n res = res / i * (i - 1);\n while (x % i == 0) x /= i;\n }\n if (x > 1) res = res / x * (x - 1);\n\n return res;\n}\n",
"description": "int phi - 欧拉函数"
},
"get_eulers - 线性筛欧拉函数": {
"prefix": "void get_eulers",
"body": "void get_eulers(int n) // 线性筛法求1~n的欧拉函数\n{\n euler[1] = 1;\n for (int i = 2; i <= n; i ++ )\n {\n if (!st[i])\n {\n primes[cnt ++ ] = i;\n euler[i] = i - 1;\n }\n for (int j = 0; primes[j] <= n / i; j ++ )\n {\n int t = primes[j] * i;\n st[t] = true;\n if (i % primes[j] == 0)\n {\n euler[t] = euler[i] * primes[j];\n break;\n }\n euler[t] = euler[i] * (primes[j] - 1);\n }\n }\n}\n",
"description": "get_eulers - 线性筛欧拉函数"
},
"void fft - FFT": {
"prefix": "void ff",
"body": "struct Complex\n{\n double x, y;\n Complex operator+ (const Complex& t) const\n {\n return {x + t.x, y + t.y};\n }\n Complex operator- (const Complex& t) const\n {\n return {x - t.x, y - t.y};\n }\n Complex operator* (const Complex& t) const\n {\n return {x * t.x - y * t.y, x * t.y + y * t.x};\n }\n};\nint rev[N], bit, tot; // tot = 1 << bit\n\nvoid fft(Complex a[], int inv)\n{\n for (int i = 0; i < tot; i ++ )\n rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));\n for (int i = 0; i < tot; i ++ )\n if (i < rev[i])\n swap(a[i], a[rev[i]]);\n for (int mid = 1; mid < tot; mid <<= 1)\n {\n auto w1 = Complex({cos(PI / mid), inv * sin(PI / mid)});\n for (int i = 0; i < tot; i += mid * 2)\n {\n auto wk = Complex({1, 0});\n for (int j = 0; j < mid; j ++, wk = wk * w1)\n {\n auto x = a[i + j], y = wk * a[i + j + mid];\n a[i + j] = x + y, a[i + j + mid] = x - y;\n }\n }\n }\n}\n",
"description": "void fft - FFT"
},
"gauss - 高斯消元(浮点值)": {
"prefix": "int gauss",
"body": "int gauss() // 高斯消元,答案存于a[i][n]中,0 <= i < n\n{\n int c, r;\n for (c = 0, r = 0; c < n; c ++ )\n {\n int t = r;\n for (int i = r; i < n; i ++ ) // 找绝对值最大的行\n if (fabs(a[i][c]) > fabs(a[t][c]))\n t = i;\n \n if (fabs(a[t][c]) < eps) continue;\n \n for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]); // 将绝对值最大的行换到最顶端\n for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c]; // 将当前行的首位变成1\n for (int i = r + 1; i < n; i ++ ) // 用当前行将下面所有的列消成0\n if (fabs(a[i][c]) > eps)\n for (int j = n; j >= c; j -- )\n a[i][j] -= a[r][j] * a[i][c];\n \n r ++ ;\n }\n \n if (r < n)\n {\n for (int i = r; i < n; i ++ )\n if (fabs(a[i][n]) > eps)\n return 2; // 无解\n return 1; // 有无穷多组解\n }\n \n for (int i = n - 1; i >= 0; i -- )\n for (int j = i + 1; j < n; j ++ )\n a[i][n] -= a[i][j] * a[j][n];\n \n return 0; // 有唯一解\n}\n",
"description": "gauss - 高斯消元(浮点值)"
},
"gauss - 高斯消元(布尔值)": {
"prefix": "int gauss",
"body": "int gauss() // 高斯消元,答案存于a[i][n]中,0 <= i < n\n{\n int c, r;\n for (c = 0, r = 0; c < n; c ++ )\n {\n int t = r;\n for (int i = r; i < n; i ++ ) // 找非零行\n if (a[i][c])\n t = i;\n\n if (!a[t][c]) continue;\n\n for (int i = c; i <= n; i ++ ) swap(a[r][i], a[t][i]); // 将非零行换到最顶端\n for (int i = r + 1; i < n; i ++ ) // 用当前行将下面所有的列消成0\n if (a[i][c])\n for (int j = n; j >= c; j -- )\n a[i][j] ^= a[r][j];\n\n r ++ ;\n }\n\n if (r < n)\n {\n for (int i = r; i < n; i ++ )\n if (a[i][n])\n return 2; // 无解\n return 1; // 有多组解\n }\n\n for (int i = n - 1; i >= 0; i -- )\n for (int j = i + 1; j < n; j ++ )\n a[i][n] ^= a[i][j] * a[j][n];\n\n return 0; // 有唯一解\n}\n",
"description": "int gauss - 高斯消元(布尔值)"
},
"int gcd - 欧几里得算法": {
"prefix": "int gcd",
"body": "int gcd(int a, int b) // 欧几里得算法\n{\n return b ? gcd(b, a % b) : a;\n}\n",
"description": "int gcd - 欧几里得算法"
},
"LL gcd - 欧几里得算法": {
"prefix": "LL gcd",
"body": "LL gcd(LL a, LL b) // 欧几里得算法\n{\n return b ? gcd(b, a % b) : a;\n}\n",
"description": "LL gcd - 欧几里得算法"
},
"int exgcd - 扩展欧几里得算法": {
"prefix": "int exgcd",
"body": "int exgcd(int a, int b, int &x, int &y) // 扩展欧几里得算法, 求x, y,使得ax + by = gcd(a, b)\n{\n if (!b)\n {\n x = 1; y = 0;\n return a;\n }\n int d = exgcd(b, a % b, y, x);\n y -= (a / b) * x;\n return d;\n}\n",
"description": "int exgcd - 扩展欧几里得算法"
},
"int lucas - Lucas定理": {
"prefix": "int lucas",
"body": "int qmi(int a, int k, int p) // 快速幂模板\n{\n int res = 1 % p;\n while (k)\n {\n if (k & 1) res = (LL)res * a % p;\n a = (LL)a * a % p;\n k >>= 1;\n }\n return res;\n}\n\nint C(int a, int b, int p) // 通过定理求组合数C(a, b)\n{\n if (a < b) return 0;\n\n LL x = 1, y = 1; // x是分子,y是分母\n for (int i = a, j = 1; j <= b; i --, j ++ )\n {\n x = (LL)x * i % p;\n y = (LL) y * j % p;\n }\n\n return x * (LL)qmi(y, p - 2, p) % p;\n}\n\nint lucas(LL a, LL b, int p)\n{\n if (a < p && b < p) return C(a, b, p);\n return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;\n}\n",
"description": "int lucas - Lucas定理"
},
"bool is_prime - 判定质数": {
"prefix": "bool is_prime",
"body": "bool is_prime(int x) // 判定质数\n{\n if (x < 2) return false;\n for (int i = 2; i <= x / i; i ++ )\n if (x % i == 0)\n return false;\n return true;\n}\n",
"description": "bool is_prime - 判定质数"
},
"void get_primes - 线性筛质数": {
"prefix": "void get_primes",
"body": "void get_primes(int n) // 线性筛质数\n{\n for (int i = 2; i <= n; i ++ )\n {\n if (!st[i]) primes[cnt ++ ] = i;\n for (int j = 0; primes[j] <= n / i; j ++ )\n {\n st[primes[j] * i] = true;\n if (i % primes[j] == 0) break;\n }\n }\n}\n",
"description": "void get_primes - 线性筛质数"
},
"int qmi - 快速幂": {
"prefix": "int qmi",
"body": "int qmi(int a, int k, int p) // 求a^k mod p\n{\n int res = 1 % p;\n while (k)\n {\n if (k & 1) res = (LL)res * a % p;\n a = (LL)a * a % p;\n k >>= 1;\n }\n return res;\n}\n",
"description": "int qmi - 快速幂"
},
"int quick_power - 快速幂": {
"prefix": "int quick_power",
"body": "int quick_power(int a, int k, int p) // 求a^k mod p\n{\n int res = 1 % p;\n while (k)\n {\n if (k & 1) res = (LL)res * a % p;\n a = (LL)a * a % p;\n k >>= 1;\n }\n return res;\n}\n",
"description": "int quick_power - 快速幂"
},
"int main - 主函数": {
"prefix": "int main()",
"body": "int main(){\n $0\n\n return 0;\n}",
"description": "int main - 主函数"
},
"simulate_anneal - 模拟退火": {
"prefix": "void sim",
"body": "double calc()\n{\n // TODO: 计算当前方案的值\n \n ans = min(ans, res); // 更新全局答案\n return res;\n}\n\nvoid simulate_anneal() // 模拟退火\n{\n for (double t = 1e6; t > 1e-6; t *= 0.95) // 逐渐降温\n {\n double x = calc(); // 原方案的值\n // TODO: 随机一个新方案\n double y = calc(); // 新方案的值\n double delta = y - x;\n \n // 新方案更好,则必选新方案;否则以一定概率选新方案 \n if (exp(-delta / t) > (double)rand() / RAND_MAX)\n {\n // TODO: 换成新方案\n }\n }\n}\n",
"description": "simulate_anneal - 模拟退火"
},
"const int N = ": {
"prefix": "const int N",
"body": "const int N = 1e5",
"description": "const int N = 1e5"
},
"const double eps = 1e-8;": {
"prefix": "const double eps ",
"body": "const double eps = 1e-8;\n",
"description": "const double eps = 1e-8;"
},
"const double PI = acos(-1);": {
"prefix": "const double PI = acos(-1)",
"body": "const double PI = acos(-1);\n",
"description": "const double PI = acos(-1);"
},
"int h[N]...邻接表不带权": {
"prefix": "int h",
"body": "int h[N], e[M], ne[M], idx;\n",
"description": "int h[N]...邻接表不带权"
},
"int h[N]...邻接表spfa": {
"prefix": "int h",
"body": "int h[N], e[M], w[M], ne[M], idx;\nint q[N], dist[N];\nbool st[N];\n",
"description": "int h[N]...邻接表spfa"
},
"int h[N]...邻接表dijkstra": {
"prefix": "int h",
"body": "int h[N], e[M], w[M], ne[M], idx;\nint dist[N];\nbool st[N];\n",
"description": "int h[N]...邻接表dijkstra"
},
"int h[N]...邻接表最大流": {
"prefix": "int h",
"body": "int h[N], e[M], f[M], ne[M], idx;\nint q[N], d[N], pre[N];\nbool st[N];\n",
"description": "int h[N]...邻接表最大流"
},
"int h[N]...邻接表费用流": {
"prefix": "int h",
"body": "int h[N], e[M], f[M], w[M], ne[M], idx;\nint q[N], d[N], pre[N], incf[N];\nbool st[N];\n",
"description": "int h[N]...邻接表费用流"
},
"int h[N]...邻接表tarjan-scc": {
"prefix": "int h",
"body": "int h[N], e[M], ne[M], idx;\nint dfn[N], low[N], timestamp; // 时间戳\nint stk[N], top;\nbool in_stk[N];\nint id[N], scc_cnt; // 每个点所属分量编号\n",
"description": "int h[N]...邻接表tarjan-scc"
},
"int h[N]...邻接表tarjan-e-dcc": {
"prefix": "int h",
"body": "int h[N], e[M], ne[M], idx;\nint dfn[N], low[N], timestamp; // 时间戳\nint stk[N], top;\nint id[N], dcc_cnt; // 每个点所属分量编号\nbool is_bridge[M];\n",
"description": "int h[N]...邻接表tarjan-e-dcc"
},
"int h[N]...邻接表tarjan-v-dcc": {
"prefix": "int h",
"body": "int h[N], e[M], ne[M], idx;\nint dfn[N], low[N], timestamp; // 时间戳\nint stk[N], top;\nint dcc_cnt;\nvector<int> dcc[N]; // 每个分量有哪些点\nbool cut[N]; // 是否为割点\nint root;\n",
"description": "int h[N]...邻接表tarjan-v-dcc"
},
"#define x first": {
"prefix": "#define x first",
"body": "#define x first\n",
"description": "#define x first"
},
"#define y second": {
"prefix": "#define y second",
"body": "#define y second\n",
"description": "#define y second"
},
"#include - 常用头文件": {
"prefix": "#include ",
"body": "#include <iostream>\n#include <cstring>\n#include <algorithm>\nusing namespace std;\n",
"description": "#include - 常用头文件"
},
"#include <vector>": {
"prefix": "#include <vector>",
"body": "#include <vector>\n",
"description": "#include <vector>"
},
"#include <queue>": {
"prefix": "#include <queue>",
"body": "#include <queue>\n",
"description": "#include <queue>"
},
"#include <cmath>": {
"prefix": "#include <cmath>",
"body": "include <cmath>\n",
"description": "#include <cmath>"
},
"#include <unordered_map>": {
"prefix": "#include <unordered_map>",
"body": "#include <unordered_map>\n",
"description": "#include <unordered_map>"
},
"#include <unordered_set>": {
"prefix": "#include <unordered_set>",
"body": "#include <unordered_set>\n",
"description": "#include <unordered_set>"
},
"#include <map>": {
"prefix": "#include <map>",
"body": "#include <map>\n",
"description": "#include <map>"
},
"#include <set>": {
"prefix": "#include <set>",
"body": "#include <set>\n",
"description": "#include <set>"
},
"#include <sstream>": {
"prefix": "#include <sstream>",
"body": "#include <sstream>\n",
"description": "#include <sstream>"
},
"#pragma GCC optimize(2)": {
"prefix": "#pragma GCC optimize(2)",
"body": "#pragma GCC optimize(2)\n",
"description": "#pragma GCC optimize(2)"
},
"#pragma GCC optimize(3)": {
"prefix": "#pragma GCC optimize(3)",
"body": "#pragma GCC optimize(3)\n",
"description": "#pragma GCC optimize(3)"
},
"typedef long long LL;": {
"prefix": "typedef long long LL",
"body": "typedef long long LL;\n",
"description": "typedef long long LL;"
},
"typedef pair<int, int> PII;": {
"prefix": "typedef pair<int, int> PII",
"body": "typedef pair<int, int> PII;\n",
"description": "typedef pair<int, int> PII;"
},
"typedef pair<double, double> PDD;": {
"prefix": "typedef pair<double, double> PDD;",
"body": "typedef pair<double, double> PDD;\n",
"description": "typedef pair<double, double> PDD;"
},
"typedef unsigned long long ULL;": {
"prefix": "typedef unsigned long long ULL",
"body": "typedef unsigned long long ULL;\n",
"description": "typedef unsigned long long ULL;"
},
"using namespace std;": {
"prefix": "using namespace std",
"body": "using namespace std;\n",
"description": "using namespace std;"
},
}
本文来自博客园,作者:喝茶看猴戏,转载请注明原文链接:https://www.cnblogs.com/zdwzdwzdw/p/17487974.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号