高级数据结构-线段树
文章目录

AcWing 1275. 最大值
单点修改,单点查询
题目链接:acwing1275 最大值
题解

代码
#include <algorithm>
#include <cstdio>
#include <iostream>
using namespace std;
const int N = 200010;
int m, p;
struct Node {
int l, r;
int v; // [l,r]最大值
} tr[4 * N];
// 由子节点的信息,来计算父节点的信息
void pushup(int u) { tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v); }
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
// 查询l,r最大值
int query(int u, int l, int r) {
// 树中节点,已经被完全包含在[l, r]中了
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int mid = tr[u].l + tr[u].r >> 1;
int v = 0;
if (l <= mid) v = query(u << 1, l, r);
if (r > mid) v = max(v, query(u << 1 | 1, l, r));
return v;
}
// 修改x位位置值为v
void modify(int u, int x, int v) {
if (tr[u].l == x && tr[u].r == x) {
tr[u].v = v;
return;
}
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid)
modify(u << 1, x, v);
else
modify(u << 1 | 1, x, v);
pushup(u);
}
// 输入代码
int main() {
scanf("%d%d", &m, &p);
int n = 0, last = 0;
build(1, 1, m);
int x;
char op[2];
while (m--) {
scanf("%s%d", op, &x);
if (*op == 'Q') {
last = query(1, n - x + 1, n);
printf("%d\n", last);
} else {
modify(1, n + 1, (last + x) % p);
n++;
}
}
return 0;
}
AcWing 245. 你能回答这些问题吗
题解
单点修改,区间查询
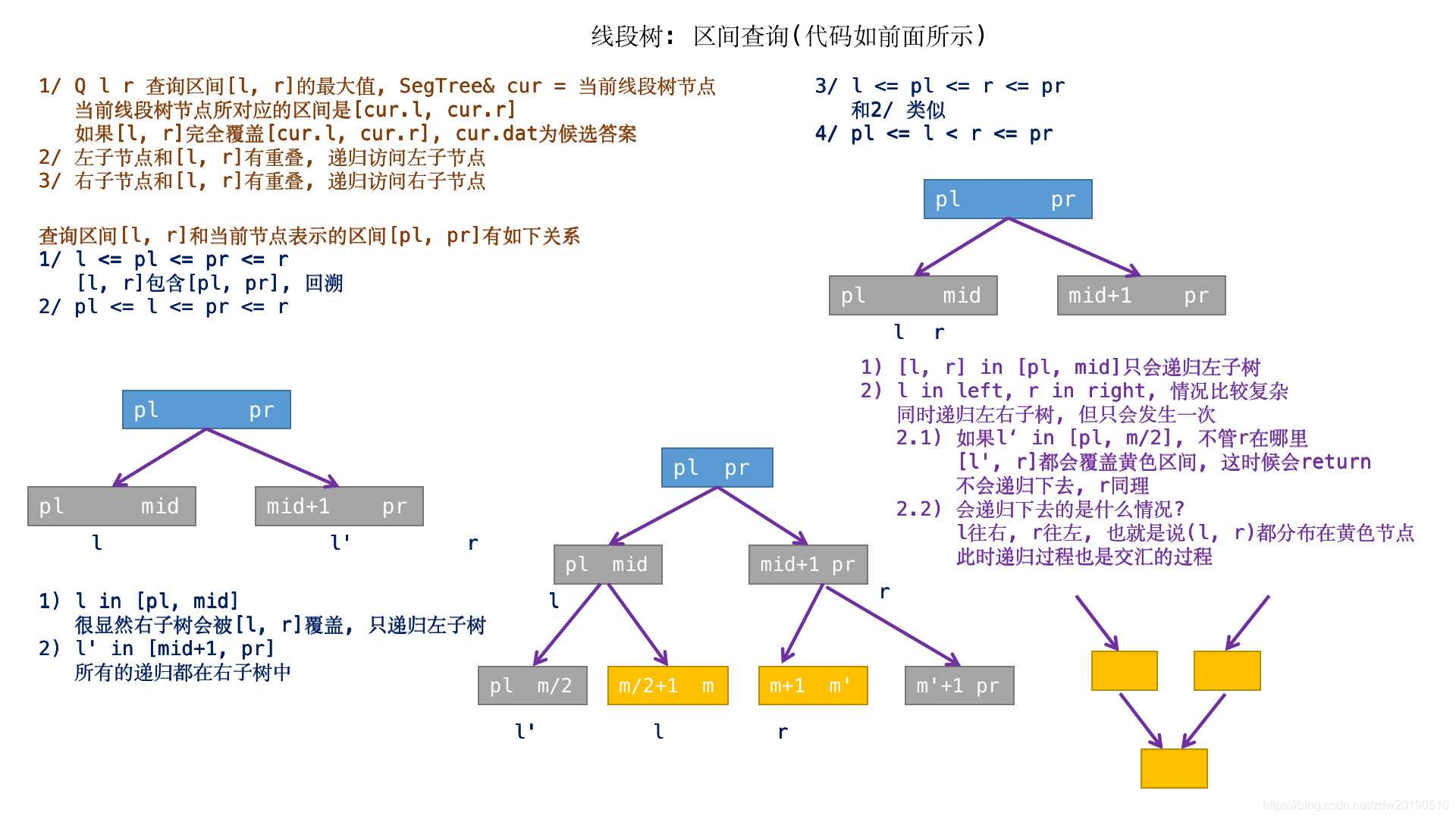
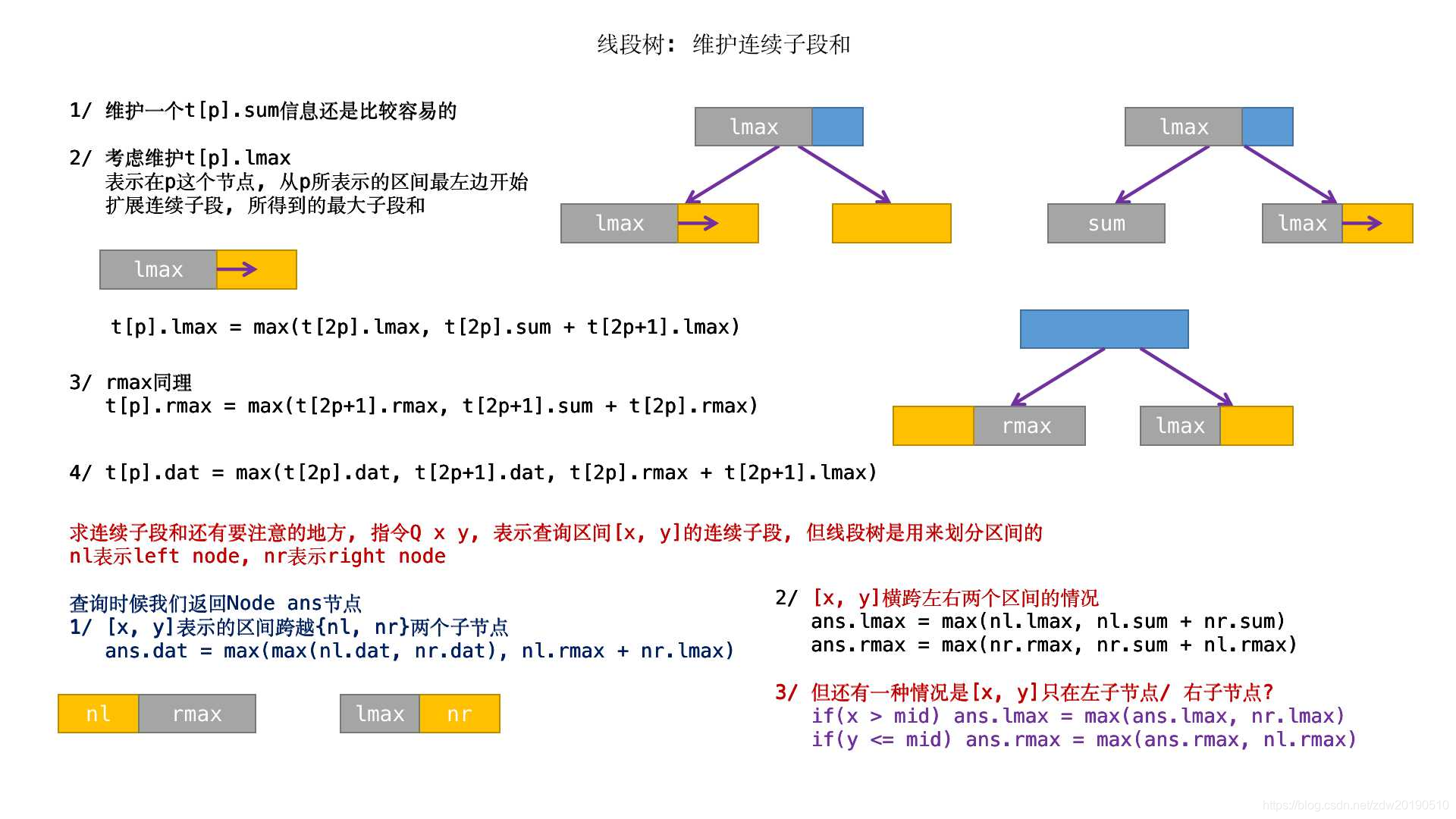
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 500010;
int n, m;
int w[N];
struct Node
{
int l, r;
int sum, lmax, rmax, tmax;
}tr[N * 4];
void pushup(Node &u, Node &l, Node &r)
{
u.sum = l.sum + r.sum;
u.lmax = max(l.lmax, l.sum + r.lmax);
u.rmax = max(r.rmax, r.sum + l.rmax);
u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
}
void pushup(int u)
{
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void build(int u, int l, int r)
{
if (l == r) tr[u] = {l, r, w[r], w[r], w[r], w[r]};
else
{
tr[u] = {l, r};
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void modify(int u, int x, int v)
{
if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v, v, v, v};
else
{
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(u << 1, x, v);
else modify(u << 1 | 1, x, v);
pushup(u);
}
}
Node query(int u, int l, int r)
{
if (tr[u].l >= l && tr[u].r <= r) return tr[u];
else
{
int mid = tr[u].l + tr[u].r >> 1;
if (r <= mid) return query(u << 1, l, r);
else if (l > mid) return query(u << 1 | 1, l, r);
else
{
auto left = query(u << 1, l, r);
auto right = query(u << 1 | 1, l, r);
Node res;
pushup(res, left, right);
return res;
}
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
build(1, 1, n);
int k, x, y;
while (m -- )
{
scanf("%d%d%d", &k, &x, &y);
if (k == 1)
{
if (x > y) swap(x, y);
printf("%d\n", query(1, x, y).tmax);
}
else modify(1, x, y);
}
return 0;
}
AcWing 246. 区间最大公约数
原题链接:AcWing 246. 区间最大公约数
题解
区间修改,区间查询公约数

代码
#include <iostream>
using namespace std;
const int N = 500010;
typedef long long LL;
struct Node {
LL l, r, sum, d;
} tr[4 * N];
LL w[N], m, n;
LL gcd(LL a, LL b) {
return b ? gcd(b, a % b) : a;
}
void pushUp(Node &u, Node &l, Node &r) {
u.sum = l.sum + r.sum;
u.d = gcd(l.d, r.d);
}
void pushUp(LL u) {
return pushUp(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void build(LL u, LL l, LL r) {
if (l == r) {
LL b = w[r] - w[r - 1];
tr[u] = {l, r, b, b};
} else {
tr[u].l = l, tr[u].r = r;
LL mid = (l + r) >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushUp(u);
}
}
void modify(LL u, LL x, LL v) {
if (tr[u].l == x && tr[u].r == x) {
LL b = tr[u].sum + v;
tr[u] = {x, x, b, b};
} else {
LL mid = (tr[u].l + tr[u].r) >> 1;
if (x <= mid) modify(u << 1, x, v);
else modify(u << 1 | 1, x, v);
pushUp(u);
}
}
Node query(LL u, LL l, LL r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u];
else {
LL mid = (tr[u].l + tr[u].r) >> 1;
if (r <= mid) return query(u << 1, l, r);
else if (l > mid) return query(u << 1 | 1, l, r);
else {
Node left = query(u << 1, l, r), right = query(u << 1 | 1, l, r);
Node res{};
pushUp(res, left, right);
return res;
}
}
}
int main() {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; i++) scanf("%lld", &w[i]);
build(1, 1, n);
LL l, r, d;
char op[2];
while (m--) {
scanf("%s%lld%lld", op, &l, &r);
if (*op == 'Q') {
Node left = query(1, 1, l), right = Node({0, 0, 0, 0});
if (l + 1 <= r) right = query(1, l + 1, r);
printf("%lld\n", abs(gcd(left.sum, right.d)));
} else {
scanf("%lld", &d);
modify(1, l, d);
if (r + 1 <= n) modify(1, r + 1, -d);
}
}
return 0;
}
AcWing 243. 一个简单的整数问题2
题解
线段树的完整代码敲一遍
代码
#include <cstdio>
const int N = 100010;
typedef long long LL;
int w[N], m, n;
struct Node {
int l, r;
LL sum, add;
} tr[4 * N];
void pushup(int u) {
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u) {
Node &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
if (root.add) {
left.add += root.add, left.sum += (left.r - left.l + 1ll) * root.add;
right.add += root.add, right.sum += (right.r - right.l + 1ll) * root.add;
root.add = 0;
}
}
void build(int u, int l, int r) {
if (l == r) {
tr[u] = {l, r, w[l], 0};
} else {
tr[u] = {l, r};
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void modify(int u, int l, int r, int d) {
if (tr[u].l >= l && tr[u].r <= r) {
tr[u].sum += (tr[u].r - tr[u].l + 1ll) * d;
tr[u].add += d;
} else {
// 此时是需要分裂修改了,需要pushdown一下
pushdown(u);
int mid = tr[u].r + tr[u].l >> 1;
if (l <= mid)
modify(u << 1, l, r, d);
if (r > mid)
modify(u << 1 | 1, l, r, d);
pushup(u);
}
}
LL query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r)
return tr[u].sum;
// 查询了,也是分裂查询,先pushdown一下
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
LL sum = 0;
if (l <= mid)
sum += query(u << 1, l, r);
if (r > mid)
sum += query(u << 1 | 1, l, r);
return sum;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", &w[i]);
build(1, 1, n);
char op[2];
int l, r, d;
while (m--) {
scanf("%s", op);
if (op[0] == 'Q') {
scanf("%d%d", &l, &r);
printf("%lld\n", query(1, l, r));
} else {
scanf("%d%d%d", &l, &r, &d);
modify(1, l, r, d);
}
}
return 0;
}
AcWing 247. 亚特兰蒂斯
扫描线
原题链接:AcWing 247. 亚特兰蒂斯


输入样例:
2
10 10 20 20
15 15 25 25.5
0
输出样例:
Test case #1
Total explored area: 180.00
样例解释
样例所示地图覆盖区域如下图所示,两个矩形区域所覆盖的总面积,即为样例的解。
题目给了n个矩形,每个矩形给了左下角和右上角的坐标,矩形可能会重叠,求的是矩形最后的面积。因为变化范围比较大,我们要用到离散化,离散化就不说了,重点说一说扫描线的过程:
下面有个矩形

题解

现在假设我们有一根线,从下往上开始扫描





- 如图所示,我们可以把整个矩形分成如图各个颜色不同的小矩形,那么这个小矩形的高就是我们扫过的距离,那么剩下了一个变量,那就是矩形的长一直在变化。
- 我们的线段树就是为了维护矩形的长,我们给每一个矩形的上下边进行标记,下面的边标记为1,上面的边标记为-1,每遇到一个矩形时,我们知道了标记为1的边,我们就加进来这一条矩形的长,等到扫描到-1时,证明这一条边需要删除,就删去,利用1和-1可以轻松的到这种状态。
还要注意这里的线段树指的并不是线段的一个端点,而指的是一个区间,所以我们要计算的时候r+1和r-1 - 再提一下离散化,离散化就是把一段很大的区间映射到一个小区间内,这样会节省大量空间,要进行离散化,我们先对端点进行排序,然后去重,然后二分找值就可以了
代码
// 看书+视频解答,扫描线
#include <algorithm>
#include <cstdio>
#include <vector>
const int N = 10010;
using namespace std;
struct Segment {
double x, y1, y2;
int k;
bool operator<(const Segment &t) const {
return x < t.x;
}
} seg[N * 2];
struct Node {
int l, r, cnt;
double len;
} tr[N * 8];
vector<double> ys;
int n;
int find(double y) {
return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}
void build(int u, int l, int r) {
tr[u] = {l, r, 0, 0};
if (l != r) {
int mid = (l + r) >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
}
void pushup(int u) {
if (tr[u].cnt) tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];
else if (tr[u].l != tr[u].r) tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
else tr[u].len = 0;
}
void modify(int u, int l, int r, int k) {
if (tr[u].l >= l && tr[u].r <= r) {
tr[u].cnt += k;
pushup(u);
} else {
int mid = (tr[u].l + tr[u].r) >> 1;
if (l <= mid) modify(u << 1, l, r, k);
if (r > mid) modify(u << 1 | 1, l, r, k);
pushup(u);
}
}
int main() {
int T = 1;
double x1, y1, x2, y2;
while (scanf("%d", &n), n) {
ys.clear();
for (int j = 0, i = 0; i < n; i++) {
scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
seg[j++] = {x1, y1, y2, 1};
seg[j++] = {x2, y1, y2, -1};
ys.push_back(y1), ys.push_back(y2);
}
sort(ys.begin(), ys.end());
ys.erase(unique(ys.begin(), ys.end()), ys.end());
build(1, 0, ys.size() - 2);
sort(seg, seg + n * 2);
double res = 0;
for (int i = 0; i < n * 2; i++) {
res += tr[1].len * (seg[i].x - seg[i - 1].x);
modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);
}
printf("Test case #%d\nTotal explored area: %.2lf\n\n", T++, res);
}
return 0;
}
AcWing 1277. 维护序列
原题链接:AcWing 1277. 维护序列

题解
由于乘法和加法两种修改,lazy标记不能确定的指出当前待修改的操作是乘法在前还是加法在前,亦或是两者混合存在,所以我们标记两个 lazy:add 和 mul.
更新的时候add更新为add×mul′+add′ ,mul 更新为mul×mul′+add′ ,sum
更新为sum×mul+add∗(u.len)
代码
// 打卡链接:https://www.acwing.com/activity/content/code/content/1082167/
#include <istream>
using namespace std;
const int N = 1e5 + 4;
typedef long long LL;
struct Node {
int l, r;
LL sum, mul, add;
Node(int l, int r, LL sum, LL add, LL mul)
: l(l), r(r), mul(mul), add(add), sum(sum) {}
Node() {}
} tr[N * 4];
int w[N];
int n, p, m;
void pushup(int u) { tr[u].sum = (tr[u << 1].sum + tr[u << 1 | 1].sum) % p; }
void eval(Node &t, int add, int mul) {
t.sum = (t.sum * mul + (t.r - t.l + 1ll) * add) % p;
t.mul = t.mul * mul % p;
t.add = (t.add * mul + add) % p;
}
void pushdown(int u) {
// 传递给左右儿子
eval(tr[u << 1], tr[u].add, tr[u].mul);
eval(tr[u << 1 | 1], tr[u].add, tr[u].mul);
// 清空标记
tr[u].add = 0, tr[u].mul = 1;
}
void build(int u, int l, int r) {
if (l == r)
tr[u] = Node(l, r, w[l], 0, 1);
else {
tr[u] = Node(l, r, 0, 0, 1);
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void modify(int u, int l, int r, int add, int mul) {
if (tr[u].l >= l && tr[u].r <= r)
eval(tr[u], add, mul);
else {
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) modify(u << 1, l, r, add, mul);
if (r > mid) modify(u << 1 | 1, l, r, add, mul);
pushup(u);
}
}
int query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
int sum = 0;
if (mid >= l) sum = query(u << 1, l, r);
if (r > mid) sum = (0ll + sum + query(u << 1 | 1, l, r)) % p;
return sum;
}
int main() {
scanf("%d%d", &n, &p);
for (int i = 1; i <= n; i++)
scanf("%d", &w[i]);
build(1, 1, n);
scanf("%d", &m);
for (int i = 0, t, g, c, op; i < m; i++) {
scanf("%d%d%d", &op, &t, &g);
if (op == 1) {
scanf("%d", &c);
modify(1, t, g, 0, c);
} else if (op == 2) {
scanf("%d", &c);
modify(1, t, g, c, 1);
} else {
printf("%d\n", query(1, t, g));
}
}
return 0;
}
总结
线段树支持单点修改,单点查询,区间修改,区间查询
pushup:子节点更新父节点
pushdown:把懒标记向下传
build:初始化一颗树
modify:修改一个区间
query:查询一个区间
push_down:区间修改,懒标记
节点存储信息:
- l,r表示区间的左右
- sum:当前区间的总和
- add: 懒标记,给以当前节点为根的子树中的每一个节点(不包含根节点,也可包含,这里是不包含)加上 add,凡是需要裂开的时候就往下面传,保证标记适用于整个区间。
void pushdown(int u) {
Node &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
if (root.add) {
left.add += root.add, left.sum += (left.r - left.l + 1ll) * root.add;
right.add += root.add, right.sum += (right.r - right.l + 1ll) * root.add;
root.add = 0;
}
}
本文来自博客园,作者:喝茶看猴戏,转载请注明原文链接:https://www.cnblogs.com/zdwzdwzdw/p/15914671.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号