8.8模拟赛总结
T1:

直接秒,维护可删除并查集即可
好像在赛场上犯了一个很唐的问题(好像是忘输入了?),然后就花了1h中途输入法还坏了,运气非常不好
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2005,M=4e6+5,inf=1e9;
int n,m,ans1,ans=inf;
int fa[M],siz[M],a[N][N];
char s[N];
struct delate{
int x,y,sz;
};
vector<delate>del;
int id(int i,int j){
if(i>n||i<1||j>m||j<1) return 0;
return (i-1)*m+j;
}
void init(){
for(int i=1;i<=n*m;i++) fa[i]=i,siz[i]=1;
}
int find(int x){
if(x==fa[x]) return x;
return find(fa[x]);
}
void merge(int x,int y,int op){
int xx=find(x),yy=find(y);
if(xx==yy) return;
if(siz[xx]>siz[yy]) swap(xx,yy);
if(op) del.push_back({xx,yy,siz[yy]});
siz[yy]+=siz[xx];
fa[xx]=yy;
return;
}
int main(){
freopen("plague.in","r",stdin);
freopen("plague.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%s",s+1);
for(int j=1;j<=m;j++){
if(s[j]=='0') a[i][j]=0;
else a[i][j]=1,ans1++;
}
}
init();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i][j]){
if(id(i-1,j)&&a[i-1][j]) merge(id(i-1,j),id(i,j),0);
if(id(i,j-1)&&a[i][j-1]) merge(id(i,j-1),id(i,j),0);
if(id(i+1,j)&&a[i+1][j]) merge(id(i+1,j),id(i,j),0);
if(id(i,j+1)&&a[i][j+1]) merge(id(i,j+1),id(i,j),0);
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(!a[i][j]){
if(id(i-1,j)&&a[i-1][j]) merge(id(i-1,j),id(i,j),1);
if(id(i,j-1)&&a[i][j-1]) merge(id(i,j-1),id(i,j),1);
if(id(i+1,j)&&a[i+1][j]) merge(id(i+1,j),id(i,j),1);
if(id(i,j+1)&&a[i][j+1]) merge(id(i,j+1),id(i,j),1);
ans=min(ans,siz[find(id(i,j))]);
// printf("%d %d %d %d %d\n",i,j,id(i,j),find(id(i,j)),siz[find(id(i,j))]);
}
while(!del.empty()){
delate g=del.back();
del.pop_back();
// printf("del %d %d %d\n",g.x,g.y,g.sz);
fa[g.x]=g.x;
siz[g.y]=g.sz;
}
}
}
printf("%.9lf",(double)ans/(ans1+1));
}
T2:

T2看到了,直接就想到了找中心肯定是不好找的,所以应当从两边往中间跳,然后应该是又过了20min,观察到数据范围 1e6,可以预处理每个位置的前一个和后一个图腾的位置
其实再加一个记忆化搜索就是正解了,考虑到
\(\sum_{i=1}^n n/i=O(n\log n)\)
证明:

因为上式小于下式所以得证
所以我们加上一个记忆化搜索就可以过了此题
我考场上竟然觉得这个是暴力。。。
然后白白又想了一个小时。。。
最后也没加记忆化,但还是侥幸过了此题
用时 > 1h30min
trick+1
T3:
考场上打了10pts暴力
发现自己的快速幂不会了。。。
然后花了20分钟终于把快速幂调过了。。。
但是赛后发现挂了

原因是什么呢?
原因是考虑道它这是实数,我们考虑的不是端点之间的整数点,而是两个端点之间的段数
对于实数的思想:
我们显然不能枚举每一种情况,因为实数的数量是无穷的
所以我们可以规定一个大范围,往上加条件,然后满足某个条件的概率就可以求出来
大范围:假如我们有 \(n\) 个 \([0,m]\) 的随机实变量 \(b_1∼b_n\)
设 \(l_i^′=max(l_i,a_i−d),r_i^′=min(r_i,a_i+d)\)
设下述条件满足的概率是 \(P\):
对于所有 \(i,b_i≤b_i+1\) 且 \(b_i∈[l_i,r_i]\)
设下述条件满足的概率是 \(Q\):
对于所有 \(i,b_i≤b_i+1\) 且 \(b_i∈[l′_i,r′_i]\)
那么 \(Q/P\) 应当等于原问题的答案
注意到 \(P\) 和 \(Q\) 形式相同,现在分析如何计算 \(P\)
非常巧妙的trick
注意到 \(b_i≤b_i+1\) 是相对条件(不好满足),\(b_i∈[l_i,l_i]\) 是绝对条件(好满足)
所以我们应当遵循绝对条件,在绝对条件的各种约束下,计算满足相对条件的概率
具体计算如下

Q1:两个数取相同情况怎么办?
A1:实数有无穷个,相同概率为0
注意:在实际计算中不用算 \(m^x\) 这一项,因为 \(Q/P\) 消掉了
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1005,mod=1e9+7,M=63;
int st[M+5],f[N*2],g[N*2],l[N],r[N],dp[N*2][N],a[N];
int n,m,ans1,ans2,d;
int qp(int x,int p){
int cnt=1;
st[0]=x;
for(int i=1;i<=M;i++){
st[i]=st[i-1]*st[i-1]%mod;
}
for(int i=0;i<=M;i++){
if(1&(p>>i)) cnt=cnt*st[i]%mod;
}
return cnt;
}
int inv(int x){
return qp(x,mod-2);
}
void init(){
f[0]=1;
for(int i=1;i<=N-2;i++){
f[i]=f[i-1]*inv(i)%mod;
// printf("f=%lld\n",f[i]);
}
}
void update(int &x,int nx){
x=(x+nx)%mod;
}
int query(){
memset(g,0,sizeof(g));
memset(dp,0,sizeof(dp));
m=0;
for(int i=1;i<=n;i++){
g[++m]=l[i],g[++m]=r[i];
}
sort(g+1,g+1+m);
m=unique(g+1,g+1+m)-g-1;
dp[1][0]=1;
for(int x=1;x<m;x++){
for(int i=0;i<=n;i++){
update(dp[x+1][i],dp[x][i]);
for(int j=i+1,w=(g[x+1]-g[x]);j<=n&&(l[j]<=g[x]&&g[x+1]<=r[j]);j++,w=w*(g[x+1]-g[x])%mod){
// printf("%lld %lld %lld %lld %lld\n",x,i,j,dp[x-1][i],f[j-i]);
update(dp[x+1][j],dp[x][i]*w%mod*f[j-i]%mod);
}
}
}
// for(int x=0;x<m;x++){
// for(int i=0;i<=n;i++){
// printf("%lld ",dp[x][i]);
// }
// printf("\n");
// }
return dp[m][n];
}
signed main(){
freopen("wizard.in","r",stdin);
freopen("wizard.out","w",stdout);
scanf("%lld%lld",&n,&d);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
for(int i=1;i<=n;i++){
scanf("%lld%lld",&l[i],&r[i]);
}
init();
ans1=query();
ans2=-1;
for(int i=1;i<=n;i++){
l[i]=max(l[i],a[i]-d);
r[i]=min(r[i],a[i]+d);
if(l[i]>=r[i]) ans2=0;
}
if(ans2==-1) ans2=query();
printf("%lld",ans2*inv(ans1)%mod);
}
T4:

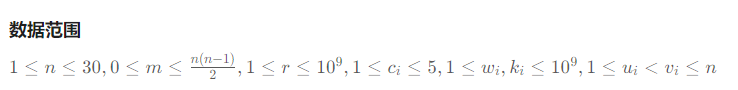
赛时背包忘了,遂放弃思考。。。
老师讲的正解正确性证明没听懂,但pjy大菊赛场上切了这道题,他的做法可能会被hack,但是看上去真的很正确,遂采用他的方法
考虑我们如果找到一条路径后,就给他转化成了一个序列上的问题
因为值域在1e9无法背包,考虑贪心,先选性价比 \(w/c\) 高的物品,但是正确性?
如果只有容量为5的背包,当w相同时,选一个c=4的不如c=2,3的更优
又考虑到c<=5,所以我们是不是可以新进行贪心,预留25格容量进行背包?
把因为n<=30,看起来就不像是什么正经的复杂度,遂考虑爆搜路径+剪枝
剪枝就是我们希望路径尽可能地长,所以如果一条边的起点不通过这条路径也能到达终点,就把它剪掉
代码:(注释地方都是调试中出现的问题)
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=35;
int n,m,r,ans;
int vis[N],e[N][N],dp[N];
struct dot{
int c,w,k;
}a[N];
vector<int>b[N];
vector<dot>S,G;
bool arr(int u,int v){
for(int i=1;i<=n;i++) vis[i]=0;
queue<int>q;
q.push(u);
while(!q.empty()){
int i=q.front();
q.pop();
for(int j=1;j<=n;j++){
if(e[i][j]&&!vis[j]){
vis[j]=1;
q.push(j);
}
}
}
if(vis[v]) return 0;
return 1;
}
bool cmp(dot i,dot j){
return i.w*j.c>j.w*i.c;
}
void solve(){
int cnt=0;
G=S;
sort(G.begin(),G.end(),cmp);
int mon=r,d=0,num=G.size()-1;
while(mon>25ll&&d<=num){
int k=min((mon-25)/G[d].c,G[d].k);
mon-=k*G[d].c;
cnt+=k*G[d].w;
if(G[d].k==k) d++;
else{
G[d].k-=k;
break;
}
}
memset(dp,0,sizeof(dp));
// printf("d %lld\n",mon);
for(int i=d;i<=num;i++){
// printf("%lld %lld %lld\n",G[i].c,G[i].w,G[i].k);
for(int j=1;j<=min(G[i].k,mon);j++){
for(int g=mon;g>=G[i].c;g--){
dp[g]=max(dp[g],dp[g-G[i].c]+G[i].w);
// printf("%lld ",dp[g]);
}
// printf("\n");
}
}
if(d<=num) cnt+=dp[mon];//万一mon很大就会RE
ans=max(cnt,ans);
}
void dfs(int u){
S.push_back(a[u]);
if(u==n){
solve();
S.pop_back();//一定要记得在return 前也要加
return;
}
for(int v:b[u]){
dfs(v);
}
S.pop_back();
}
signed main(){
freopen("rider.in","r",stdin);
freopen("rider.out","w",stdout);
scanf("%lld%lld%lld",&n,&m,&r);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&a[i].c,&a[i].w,&a[i].k);
}
for(int i=1;i<=m;i++){
int u,v;
scanf("%lld%lld",&u,&v);
e[u][v]=1;
}
for(int u=1;u<=n;u++){
for(int v=1;v<=n;v++){
if(!e[u][v]) continue;
e[u][v]=0;
if(arr(u,v)){
e[u][v]=1;
b[u].push_back(v);
}
}
}
// for(int i=1;i<=n;i++){
// for(int j:b[i]){
// printf("%d %d\n",i,j);
// }
// }
dfs(1);
if(!ans) ans=-1;
printf("%lld\n",ans);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号