可持久化数据结构

思想

以下为个人的理解，可供参考

考虑到一次修改只会影响到一个节点，那我们就直接另存一下这个节点就好了呗

但是不行，因为访问时我询问时间为 t 的节点，我找不到 t 时间这个点的改动什么的

而线段树有一个好的性质，就是它修改一个节点最多会动log个节点，其余的节点都是以前的，所以可以每一次修改，就把变化了的节点新开一棵树，以前的没有动的节点，就直接把旧节点连在新节点上就行

然后操作时你就把一个时间内的树考虑成一颗独立的树就行，其它的节点并不会产生任何影响

新思想

在写博客时，我就想，既然我们只是做不到查询t时间点修改了哪些位置

对于可持久化数组，我对每个节点开一个 vector 存储的是它变化的时间位置，对于每次查询 \(t\) 时间 \(x\) 上的位置，直接二分，找到最后一次修改，这样不行吗？

然而考虑题目是在历史版本上进行修改，也就是历史版本它也会有别的修改，你无法全部统计入档次修改，假了

主席树

用途：会在线段树上进行很多次修改，还会查询历史节点信息

然后考虑到修改一个节点，只会改变其下的log个节点，于是就新整了log个节点，建立在原树之上

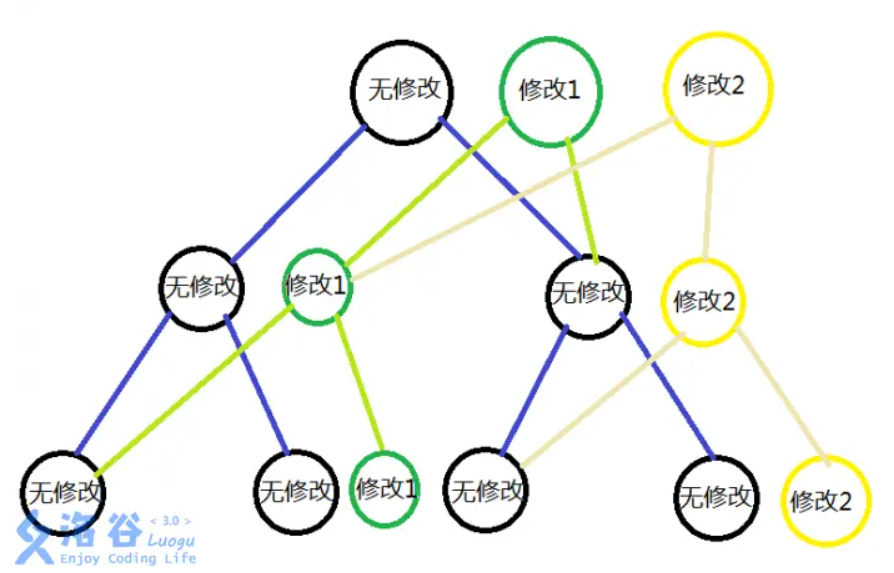
m 次修改操作，相当于是建立了 \(m\) 棵树，试想一下，你从修改一节点往下进行查询，是不是依旧是一棵树呢

代码实现（真的不难）：

void change(int k, int l, int r, int x,int v,int &g) {
        k = newnode(k);
        g = k;
        if (l == r) {
            sum(k)=v;
            return;
        }
        int mid = (l + r) >> 1;
        if (x <= mid)
            change(ls(k), l, mid, x, ls(k));
        else
            change(rs(k), mid + 1, r, x, rs(k));
        sum(k) = sum(ls(k)) + sum(rs(k));
    }
change(top[i-1],1,n,i,a[i],top[i]);//top[i-1]表示上一次修改的根节点，top[i]表示这次的根节点

T1：

区间下标为时间节点，线段树维护值域

先离散化（因为要线段树维护）

查询，就当作正常线段树上二分即可，为什么要 \(l-1,r\) 端点一起进行query呢？

因为线段树上二分，我们只知道你在这个值域区间里排老几，而想求这个值域区间有多少数，我们只能通过前缀和，同时求前缀和后缀的方法

#include<bits/stdc++.h>
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define sum(x) tr[x].sum
using namespace std;
const int N=2e5+5;
struct dot{
    int ls,rs,sum;
}tr[N*40];
int cnt,n,m,len;
int a[N],st[N];
vector<int>tmp;
struct tree{
    int newnode(int k){
        tr[++cnt]=tr[k];
        return cnt;
    }
    void change(int k,int l,int r,int x,int &g){
        k=newnode(k);
        g=k;
        if(l==r){
            sum(k)++;
            return;
        }
        int mid=(l+r)>>1;
        if(x<=mid)  change(ls(k),l,mid,x,ls(k));
        else  change(rs(k),mid+1,r,x,rs(k));
        sum(k)=sum(ls(k))+sum(rs(k));
    }
    int query(int k,int p,int l,int r,int x){
        if(l==r){
            return l;
        }
        int mid=(l+r)>>1;
        int sum=sum(ls(k))-sum(ls(p));
        if(sum>=x)  return query(ls(k),ls(p),l,mid,x);
        else  return query(rs(k),rs(p),mid+1,r,x-sum);
    }
}tree;
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        tmp.push_back(a[i]);
    }
    sort(tmp.begin(),tmp.end());
    tmp.erase(unique(tmp.begin(),tmp.end()),tmp.end());
    len=tmp.size();
    for(int i=1;i<=n;i++){
        a[i]=lower_bound(tmp.begin(),tmp.end(),a[i])-tmp.begin()+1;
    }
    for(int i=1;i<=n;i++){
        tree.change(st[i-1],1,len,a[i],st[i]);
    }
    for(int i=1;i<=m;i++){
        int l,r,k;
        scanf("%d%d%d",&l,&r,&k);
        printf("%d\n",tmp[tree.query(st[r],st[l-1],1,len,k)-1]);
    }
}

T2：

调了好久，注意，你就把split操作要分开的的地方全都复制成新节点即可（因为你的1变化一定不能影响到原来的节点）

有的题解说merge操作也要复制原来的节点，我不敢苟同这个观点，事实证明，最后我没复制也过了

一定要注意题目中的这个条件

和原本平衡树不同的一点是，每一次的任何操作都是基于某一个历史版本，同时生成一个新的版本。

点击查看代码

#include<bits/stdc++.h>
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define siz(x) tr[x].siz
#define pri(x) tr[x].pri
#define key(x) tr[x].key
using namespace std;
const int N=5e5+5,inf=2147483647;
int cnt,t,n;
int root[N];
struct dot{
    int ls,rs,siz,pri,key;
    void ins(int x){
        ls=rs=0;
        key=x;
        siz=1;
        pri=rand();
    }
}tr[N<<7];
struct tree{
    void init(){
        srand(time(NULL));
    }
    int newnode(int u){
        tr[++cnt]=tr[u];
        tr[cnt].pri=rand();
        return cnt;
    }
    int makenode(int x){
        // if(x==0)  return 0;
        tr[++cnt].ins(x);
        return cnt;
    }
    void update(int u){
        siz(u)=siz(ls(u))+siz(rs(u))+1;//+1一定注意
    }
    void split(int u,int x,int &L,int &R){
        if(u==0){
           L=R=0; 
           return;
        }  
        u=newnode(u);
        if(key(u)<=x){//
            L=u;
            split(rs(u),x,rs(u),R);
        }
        else{
            R=u;
            split(ls(u),x,L,ls(u));
        }
        update(u);
    }
    int merge(int L,int R){
        if(L==0||R==0)  return L+R;
        if(pri(L)>=pri(R)){
            // L=newnode(L);
            rs(L)=merge(rs(L),R);
            update(L);
            return L;
        }
        else{
            // R=newnode(R);
            ls(R)=merge(L,ls(R));
            update(R);
            return R;
        }
    }
    void insert(int v,int x){
        int L,R;
        split(root[v],x,L,R);
        root[++t]=merge(merge(L,makenode(x)),R);
    }
    void delite(int v,int x){
        int L,R,p;
        split(root[v],x,L,R);
        split(L,x-1,L,p);
        if(p)  p=merge(ls(p),rs(p));
        root[++t]=merge(merge(L,p),R);
    }
    int kth(int u,int k){
        if(siz(ls(u))+1==k)  return u;
        if(siz(ls(u))>=k)  return kth(ls(u),k);
        return kth(rs(u),k-siz(ls(u))-1);
    }
    int pre(int v,int x){
        int L,R,res=-inf;
        split(root[v],x-1,L,R);
        if(siz(L))  res=key(kth(L,siz(L)));//
        root[v]=merge(L,R);
        return res;
    }
    int lst(int v,int x){
        int L,R,res=inf;
        split(root[v],x,L,R);
        if(siz(R))  res=key(kth(R,1));
        root[v]=merge(L,R);
        return res;
    }
    int query(int v,int x){
        int L,R;
        split(root[v],x-1,L,R);
        int res=siz(L)+1;
        root[v]=merge(L,R);
        return res;
    }
}FHQ;
int main(){
    FHQ.init();
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        int v,op,x;
        scanf("%d%d%d",&v,&op,&x);
        if(op==1){
            FHQ.insert(v,x);
        }
        else if(op==2){
            FHQ.delite(v,x);
        }
        else{
            root[++t]=root[v];//
            if(op==3){
                printf("%d\n",FHQ.query(v,x));
            }
            else if(op==4){
                printf("%d\n",key(FHQ.kth(root[v],x)));
            }
            else if(op==5){
                printf("%d\n",FHQ.pre(v,x));
            }
            else{
                printf("%d\n",FHQ.lst(v,x));
            }
        }
        
    }
}