笛卡尔树

算法理解

解决序列上的最值问题。

本质：把序列转化成二叉堆

序列上的编号用 \(id\) 表示，每个点的权值用 \(v\) 代替

对于一个最基本的二叉结构，\(fa\) 的左右儿子分别为 \(s1,s2\)，遵循：

$s1.id < fa.id < s2.id $

\(fa.v < s1.v,s2.v\)（小根堆）

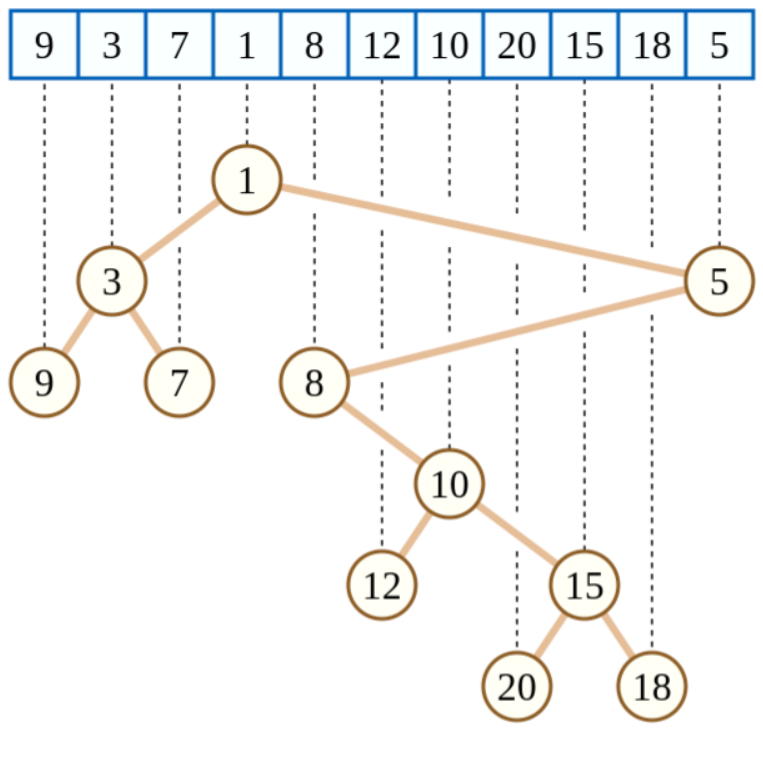
根据这种结构，得到以下性质：

1. 一个节点的左子树的所有编号小于当前节点的编号，右子树则全部大于

2. \(g1.id <= lca(g1,g2) <= g2.id\)

证明：

当 \(gcd(g1,g2)=g1/g2\) 时，显然成立

否则，\(g1\) 在 \(gcd(g1,g2)\) 的左子树上，\(g2\) 在 \(gcd(g1,g2)\) 的右子树上，根据性质 1 ，结论成立

区间求最值

区间 \((l,r)\) 求最值，找到 \(l,r\) 在区间上对应的值，在笛卡尔树上取 \(gcd(l,r)\)，根据性质 2，即得 \(gcd(l,r)\) 为区间上最值

单调栈建树

总结出的三大铁律：

1. 单调栈里记录的是最右链，栈头是链底，栈底是链首

2. 新加入的节点是它的父亲的右儿子

3. 新加入一个节点的的时候，栈内弹掉的最后一个节点是新加入点的左儿子