虚树

算法目标

现在给出一棵树，有给出一些关键点，然后现在我们只关注关键点于关键点之间的关系，也就是我们要在各个关键点之间建树，这棵树就叫虚树

实现方法

我们考虑虚树中要包含两两关键点的 \(lca\) 和它自己，然后需要将它们按照父子关系连接边建树，考虑最简单的容易表示父子关系和子树关系的东西 dfs序

把节点按照 dfs 序排好

找出一个集合 S 包含所有虚树中的点的 dfs 序，这个集合包含所有的关键点，然后考虑将两个相邻点的 lca 加入集合去重，此时这个集合必然包含所有的关键点和关键点的 lca，证明如下：

对集合 S 进行排序，我们就要考虑怎么将集合中的点建树

单调栈求法

维护一个单调递增栈，这个单调栈里面的点按照 dfs 序是连续的，我们依次按照排好序的 S 里的顺序加入把点加入栈，可以发现此时栈里的点构成了一条链，并且栈中的 \(a[i-1]\) 元素在虚树上是 \(a[i]\) 的父亲

当加入一个点时，设 \(a[top]\) 为栈顶元素，\(g\) 为当前元素，求一下 \(lca(a[top],g)\)，然后用 \(lca(a[top],g)\) 弹掉栈中大于它的元素，再加入 \(g\) 即可

当弹出栈头 \(a[top]\) 时， \(a[top-1]\) 是它的父亲，连边即可

lca连边求法（更简便）

设序列中两个相邻的点为 \(x,y\)，结论：每个 \(lca(x,y)\) 是 \(y\) 的父亲

证明：

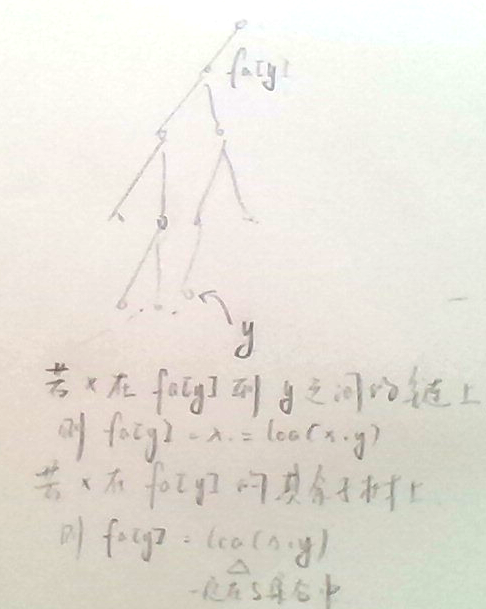
证毕。

模板代码

练习