网络流
最大流
基本概念
原点s,汇点t,流量,容量
最大流问题原型:水渠问题,有一些水渠,由很多阀门连接,阀门控制水的流速,水渠内水单向流动,给定起点和终点,求最大流速
容量:每条边最大流速
流量:每条边水的流速
最大流:从s到t的最大流量
增广路:一条从s到t的可行路径
原理
每次找到一条增广路后就将整个路径的容量减去路径上的流量,然后再在整个路径的所有边的反边的容量上加上流量
EK算法
每一次bfs找到一条最短的路径,进行增广(就是原理所述操作),直到s与t不连通,\(O(nm^2)\)
dinic算法
我们先将图用bfs分层,然后再用dfs,然而dfs的路径只能从当前层走到更深一层,我们会发现,这样找出的所有路径一定都是当前能找到的最短路径,就统一进行增广操作
如此进行多次bfs和dfs,直到s与t不连通,\(O(n^2m)\)
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=205,M=5005,inf=1e12;
int n,m,s,t,cnt=1,ans;
int head[N],dep[N],now[N];
struct Node{
int to,nxt,w;
}e[2*M];
void add(int u,int v,int w){
cnt++;
e[cnt].to=v;
e[cnt].nxt=head[u];
e[cnt].w=w;
head[u]=cnt;
}
bool bfs(){
for(int i=1;i<=n;i++) dep[i]=inf,now[i]=head[i];
dep[s]=0;
queue<int>q;
q.push(s);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=e[i].nxt){
if(e[i].w&&dep[e[i].to]==inf){
q.push(e[i].to);
dep[e[i].to]=dep[u]+1;
if(e[i].to==t) return 1;
}
}
}
return 0;
}
int dfs(int u,int sum){
if(u==t) return sum;
int flow=0;
for(int i=now[u];i&∑i=e[i].nxt){
now[u]=i;
if(e[i].w&&dep[e[i].to]==dep[u]+1){
int k=dfs(e[i].to,min(sum,e[i].w));
if(k==0) dep[e[i].to]=inf;
e[i].w-=k;e[i^1].w+=k;
flow+=k;sum-=k;
}
}
return flow;
}
signed main(){
scanf("%lld%lld%lld%lld",&n,&m,&s,&t);
for(int i=1;i<=m;i++){
int u,v,w;
scanf("%lld%lld%lld",&u,&v,&w);
add(u,v,w);add(v,u,0);
}
while(bfs()) ans+=dfs(s,inf);
printf("%lld\n",ans);
return 0;
}
经典模型
最小割
去掉一些边,使得原点到汇点不连通,求去掉的边的容量总和的最小值
定理:最大流=最小割
尝试解释,最大流相当于是利用了所有的增广路中的最小容量的那一条边,同时也覆盖了所有的增广路,使得选了这些边之后图不连通
二分图最大匹配问题
我们建一个原点,一个汇点,原点向二分图一边的所有点连一条容量为1的边,另一边的所有点向汇点连一条容量为1的边,原来图上的边容量为1,然后跑一遍网络流,就是最后的答案
尝试解释,原点向左边的点连一条容量为1的边,表示我们最多这个点最多只能选择一条边,从右边向汇点连的一条容量为1的边也是一样,相当于也是只能选一次,然后我们求出来的最大流相当于是能选的最大数量
最小点覆盖问题
题目:选定一些点使得这些点能覆盖到所有的边,求能选的最小的点
定理:最小点覆盖问题等价于二分图最大匹配问题
尝试解释
最大权闭合子图
闭合子图:对于子图内每一个点的后继节点都属于子图
问题:每一个点有权值(有正有负),然后求一个最大的闭合子图使得包含的总权值最大
首先正的越多越好,负的越少越好,根据经典套路,我们建一张二分图,正的点和原点连边边权即为点权,负的点和汇点连边,边权为点权的绝对值,然后跑一下最小割
我们考虑闭合子图,一个点如果被选了,它的后续节点,也就是所有能到达汇点的增广路就必须选所以说要么我们不选这个点,就砍掉其连向原点的边,或者说我们选这个点,但是选了的点的后续节点,就是能与它相连的点都不与汇点连通,就是砍掉那些点与汇点的边
所以说所有与原点连通的点相当于我们保留的点,与汇点连通的点就是要删去的点,然后考虑跑一遍最小割就会把图分为两部分,同时最小割的答案由两部分组成,一部分正权点,就是我们不选的正权点,删去的代价,另一部分是我们选的负权点的代价的绝对值
最后答案=正权点和-(删去的正权点代价+选择的负权点价值绝对值)=正权点和-最小割
例题
P2763 试题库问题
板子题,把题目与原点相连,类型与汇点相连,题目和对应的类型相连
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5,inf=1e9;
int k,n,cnt,s,t,m,ans;
int head[N],dep[N],now[N],w[N];
struct edge{
int to,nxt,w;
}e[10*N];
vector<int>num[N];
void add(int u,int v,int w){
e[++cnt]={v,head[u],w};
head[u]=cnt;
}
bool bfs(){
for(int i=s;i<=t;i++) dep[i]=inf,now[i]=head[i];
dep[s]=0;
queue<int>q;
q.push(s);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(dep[v]==inf&&e[i].w){
q.push(v);
dep[v]=dep[u]+1;
if(v==t) return 1;
}
}
}
return 0;
}
int dfs(int u,int sum){
if(u==t) return sum;
int flow=0;
for(int i=now[u];i&∑i=e[i].nxt){
now[u]=i;
int v=e[i].to;
if(e[i].w&&dep[v]==dep[u]+1){
int k=dfs(v,min(sum,e[i].w));
if(k==0) dep[v]=inf;
e[i].w-=k;e[i^1].w+=k;
flow+=k;sum-=k;
}
}
return flow;
}
int main(){
scanf("%d%d",&k,&n);
s=0,t=n+k+1;
for(int i=1;i<=k;i++){
scanf("%d",&w[i]);
add(n+i,t,w[i]);
add(t,n+i,0);
m+=w[i];
}
for(int i=1;i<=n;i++){
int p,r;
scanf("%d",&p);
add(s,i,1);
add(i,s,0);
while(p--){
scanf("%d",&r);
add(i,n+r,1);
add(n+r,i,0);
}
}
while(bfs()) ans+=dfs(s,inf);
if(ans!=m) printf("No Solution!");
else{
for(int i=1;i<=n;i++){
for(int j=head[i];j;j=e[j].nxt){
if(e[j].w==0&&e[j].to>n){
num[e[j].to-n].push_back(i);
}
}
}
for(int i=1;i<=k;i++){
printf("%d: ",i);
for(int g:num[i]){
printf("%d ",g);
}
printf("\n");
}
}
}
【例题1】任务分配
建图模型+1:任务放中间,然后向原点向任务流 \(b[i]\) ,任务向汇点流 \(a[i]\) 两个任务之间如果有约束,建 \(v\) 的双向边,求最小割
为什么是最小割,因为是选择总花费最小
中间建双向边的用建反边吗?
不用,我们设被连的点为 \(x,y\)
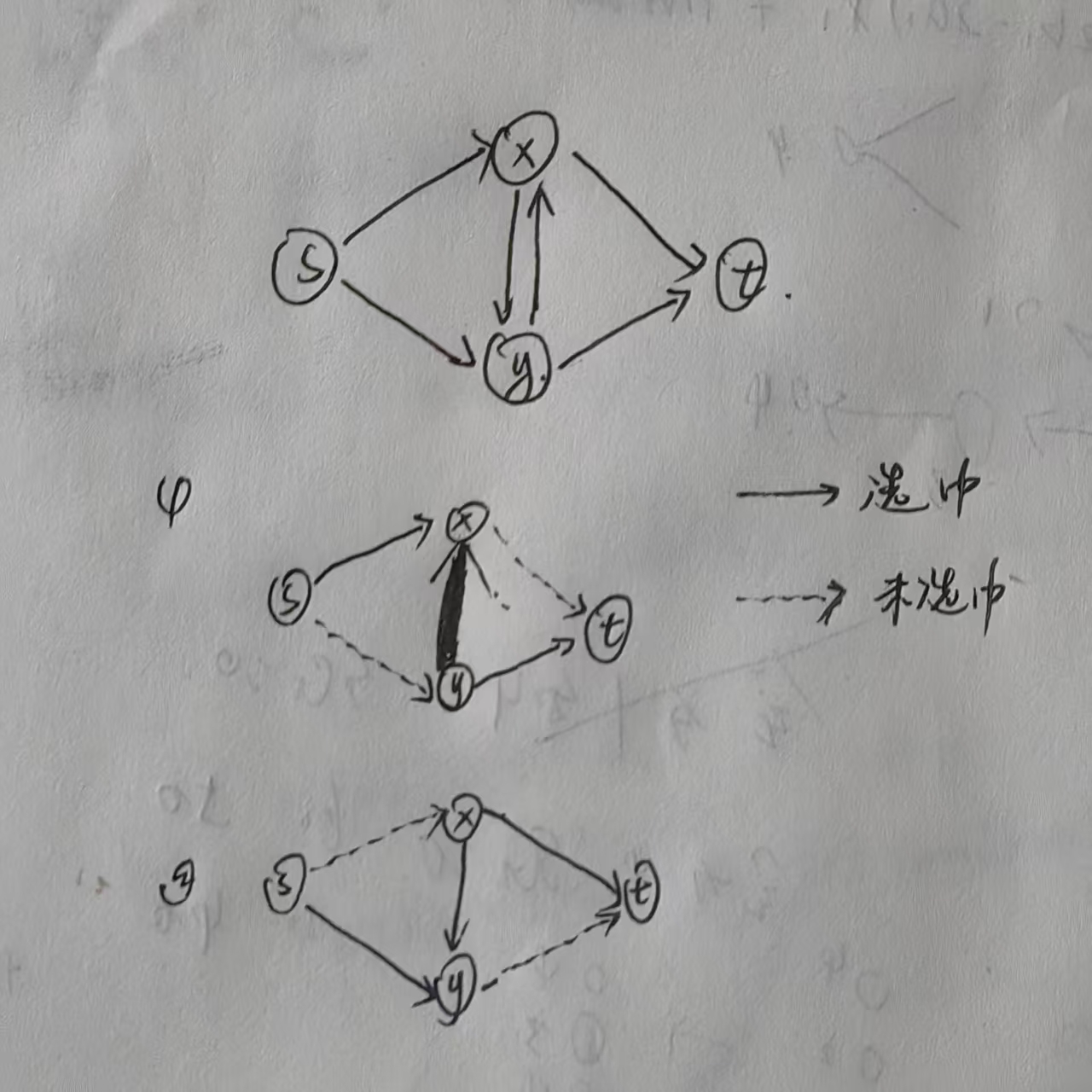
有这两种情况,我们发现,双向边正向和反向不可能同时被选择,此时流量为 \(v\) 的边的反向边就充当了0 容量的边,所以不用建反边
注意:cnt下标从0开始,因为存在权值为0的点所以head数组初始化为-1,原点向任务的流量是 \(b[i]\) ,调了好久这几个错误
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e4+5,M=5e5+5,inf=1e17;
struct edge{
int to,nxt,w;
}e[M];
int cnt,s,t,n,m,ans;
int head[N],now[N],dep[N],a[N],b[N];
void add(int u,int v,int w){
e[++cnt]={v,head[u],w};
head[u]=cnt;
}
bool bfs(){
for(int i=s;i<=t;i++) now[i]=head[i],dep[i]=inf;
dep[s]=0;
queue<int>q;
q.push(s);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i!=-1;i=e[i].nxt){
int v=e[i].to,w=e[i].w;
if(w&&dep[v]==inf){
q.push(v);
dep[v]=dep[u]+1;
if(v==t) return 1;
}
}
}
return 0;
}
int dfs(int u,int sum){
if(u==t) return sum;
int flow=0;
for(int i=now[u];i!=-1&∑i=e[i].nxt){
now[u]=i;
int v=e[i].to,w=e[i].w;
if(w&&dep[v]==dep[u]+1){
int k=dfs(v,min(sum,w));
if(k==0) dep[v]=inf;
e[i].w-=k;e[i^1].w+=k;
sum-=k;flow+=k;
}
}
return flow;
}
void init(){
cnt=-1;//从0开始
memset(head,-1,sizeof(head));
}
signed main(){
init();
scanf("%lld%lld",&n,&m);
s=0,t=n+1;
for(int i=1;i<=n;i++){
scanf("%lld%lld",&a[i],&b[i]);
add(s,i,b[i]);add(i,s,0);//说明断了一个链所以是b[i]
add(i,t,a[i]);add(t,i,0);
}
for(int i=1;i<=m;i++){
int x,y,v;
scanf("%lld%lld%lld",&x,&y,&v);
add(x,y,v);
add(y,x,v);
}
while(bfs()) ans+=dfs(s,inf);
printf("%lld\n",ans);
}
【例题2】幸福值
建议看这篇
转化思路:求最大幸福值,就用总量-最小割
然后我们套用上题的模型,往里填值,解方程即可
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int M=1e4+5,N=105,inf=1e16;
int n,m,cnt,ans1,ans,s,t;
int head[M],now[M],a[N][N],b[N][N],c1[N][N],c2[N][N],d1[N][N],d2[N][N],dep[M];
struct edge{
int to,nxt,w;
}e[20*M];
void add(int u,int v,int w){
e[cnt]={v,head[u],w};
head[u]=cnt++;
}
void init(){
memset(head,-1,sizeof(head));
}
bool bfs(){
for(int i=s;i<=t;i++) dep[i]=inf,now[i]=head[i];
dep[s]=0;
queue<int>q;
q.push(s);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i!=-1;i=e[i].nxt){
int v=e[i].to,w=e[i].w;
// printf("%d %d\n",u,v);
if(w&&dep[v]==inf){
q.push(v);
dep[v]=dep[u]+1;
if(v==t) return 1;
}
}
}
return 0;
}
int dfs(int u,int sum){
if(u==t) return sum;
int flow=0;
for(int i=now[u];i!=-1&∑i=e[i].nxt){//sum减为0时退出
now[u]=i;
int v=e[i].to,w=e[i].w;
if(w&&dep[v]==dep[u]+1){
int k=dfs(v,min(sum,w));
if(k==0) dep[v]=inf;
e[i].w-=k;e[i^1].w+=k;
flow+=k,sum-=k;
}
}
return flow;
}
int id(int x,int y){
return (x-1)*m+y;
}
signed main(){
// freopen("a.in","r",stdin);
// freopen("a.out","w",stdout);
init();
scanf("%lld%lld",&n,&m);
s=0,t=n*m+1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%lld",&a[i][j]);
ans1+=a[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%lld",&b[i][j]);
ans1+=b[i][j];
}
}
for(int i=1;i<n;i++){
for(int j=1;j<=m;j++){
scanf("%lld",&c1[i][j]);
ans1+=c1[i][j];
}
}
for(int i=1;i<n;i++){
for(int j=1;j<=m;j++){
scanf("%lld",&d1[i][j]);
ans1+=d1[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<m;j++){
scanf("%lld",&c2[i][j]);
ans1+=c2[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<m;j++){
scanf("%lld",&d2[i][j]);
ans1+=d2[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int u=id(i,j),v;
add(s,u,2*a[i][j]+c1[i][j]+c1[i-1][j]+c2[i][j]+c2[i][j-1]);//c1,d1都是i操作,并且要-1
add(u,s,0);
add(u,t,2*b[i][j]+d1[i][j]+d1[i-1][j]+d2[i][j]+d2[i][j-1]);
add(t,u,0);
if(i!=n){
v=id(i+1,j);
add(u,v,c1[i][j]+d1[i][j]);
add(v,u,c1[i][j]+d1[i][j]);
}
if(j!=m){
v=id(i,j+1);
add(u,v,c2[i][j]+d2[i][j]);
add(v,u,c2[i][j]+d2[i][j]);
}
}
}
while(bfs()) ans+=dfs(s,inf);
printf("%lld\n",ans1-ans/2);
}
T3:
切了
但是输出有一点问题
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int M=1e4+5,N=105,inf=1e13;
int n,m,cnt,ans1,ans,s,t;
int head[M],now[M],dep[M],val[M],w[M],vis1[M],vis2[M];
struct edge{
int to,nxt,w;
}e[M];
void add(int u,int v,int w){
e[cnt]={v,head[u],w};
head[u]=cnt++;
}
void init(){
memset(head,-1,sizeof(head));
s=0,t=m+n+1;
}
bool bfs(){
for(int i=s;i<=t;i++) dep[i]=inf,now[i]=head[i];
dep[s]=0;
queue<int>q;
q.push(s);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i!=-1;i=e[i].nxt){
int v=e[i].to,w=e[i].w;
// printf("%lld %lld\n",u,v);
if(w&&dep[v]==inf){
q.push(v);
dep[v]=dep[u]+1;
if(v==t) return 1;
}
}
}
return 0;
}
int dfs(int u,int sum){
if(u==t) return sum;
int flow=0;
for(int i=now[u];i!=-1&∑i=e[i].nxt){//sum减为0时2退出
now[u]=i;
int v=e[i].to,w=e[i].w;
if(w&&dep[v]==dep[u]+1){
int k=dfs(v,min(sum,w));
if(k==0) dep[v]=inf;
e[i].w-=k;e[i^1].w+=k;
flow+=k,sum-=k;
}
}
return flow;
}
void read(int i){
char tools[10000];
memset(tools,0,sizeof tools);
cin.getline(tools,10000);
int ulen=0,tool;
while (sscanf(tools+ulen,"%lld",&tool)==1)//之前已经用scanf读完了赞助商同意支付该实验的费用
{//tool是该实验所需仪器的其中一个
//这一行,你可以将读进来的编号进行储存、处理,如连边。
int v=tool+m;
add(i,v,inf);
add(v,i,0);
if (tool==0)
ulen++;
else {
while (tool) {
tool/=10;
ulen++;
}
}
ulen++;
}
}
void visit(){
for(int i=head[s];i!=-1;i=e[i].nxt){
// printf("fff %d %d\n",e[i].to,e[i].w);
if(!e[i].w) vis1[e[i].to]=1;
}
for(int i=head[t];i!=-1;i=e[i].nxt){
// printf("%d %d\n",e[i].to-m,e[i].w);
if(e[i].w) vis2[e[i].to-m]=1;
}
}
signed main(){
// freopen("b.in","r",stdin);
// freopen("b.out","w",stdout);
scanf("%lld%lld",&m,&n);
init();
for(int i=1;i<=m;i++){
scanf("%lld",&val[i]);
ans1+=val[i];
add(s,i,val[i]);
add(i,s,0);
read(i);
}
for(int i=1;i<=n;i++){
scanf("%lld",&w[i]);
int v=i+m;
add(v,t,w[i]);
add(t,v,0);
}
while(bfs()) ans+=dfs(s,inf);
visit();
for(int i=1;i<=m;i++) if(dep[i]!=inf) printf("%d ",i);
printf("\n");
for(int i=1;i<=n;i++) if(dep[i+m]!=inf) printf("%d ",i);
printf("\n");
printf("%lld",ans1-ans);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号