关于简单线性代数——矩阵乘法与行列式
惨淡经营中...（过几天同学们就要去参加中考了诶 ##狗头## 好紧张！！！真替他们紧张，还好我不用考！）
今天记录的是矩阵乘法还有行列式求值
矩阵：就像二维数组一样，是一个以长方形排列的集合。
矩阵乘法：
对于两个矩阵A和B：
将他们相乘的结果记为C
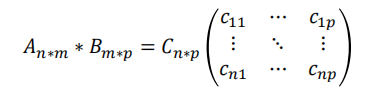
不难发现，C的行数与A的行数相同，C的列数与B的列数相同，A的列数与B的行数相同。
那怎么求出C中的元素呢？
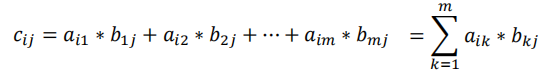
举个简单的例子：
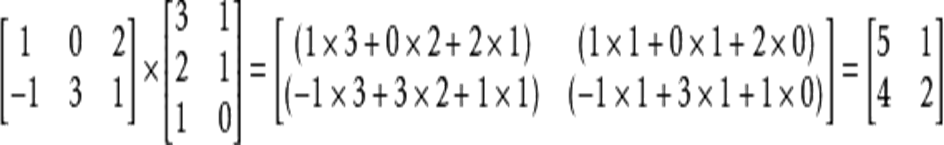
咳咳，矩阵乘法满足的运算性质有：矩阵间的乘法结合律、数乘和矩阵乘结合律、矩阵间的乘法分配律，但是不满足乘法交换律！！
若矩阵A是n阶方阵，那么A的i次幂乘A的j次幂就是A的i+j次幂，A的i次幂的j次幂等于A的ij次幂。
矩阵转置：把矩阵 A 的行换成同序数的列得到的新矩阵，叫做A的转置矩阵，记作AT。
转置矩阵的运算性质：
1、（AT）T=A
2、（A+B）T=AT+BT
3、
4、（AB）T=BTAT
矩阵加法：
对于两个形状相同的矩阵A，B：
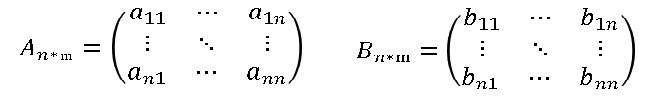
设两集合之和组成的集合为C：
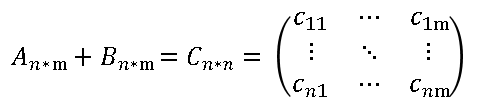
C中每个元素都是A、B集合相应位置的元素之和，即：
嘿嘿，如果这个矩阵的行数和列数均等于n，那我们就叫他n阶方阵，记作
只有一行的就是行矩阵，只有一列的就是列矩阵，元素全是0的叫做零矩阵
如果两个矩阵行数列数均相同，他们就成为同型矩阵
如果两个同型矩阵的对应元素相等，那这两个矩阵就相等
如果A是一个n阶方阵，如果满足：A=AT，即aij=aji，那么A就是一个对称阵
如果A=-AT，那么A就是反对称阵。
很显然，对称阵的特点就是沿着从左上角到右下角的对角线，其两侧对称。
而对于反对称矩阵，就要满足对角线上的元素都为0，且关于对称轴位置对称的两个元素，其互为相反数。
行列式：有点难解释，下面会有所体现的
行列式求值：
如图：对于行列式A，他的值为：
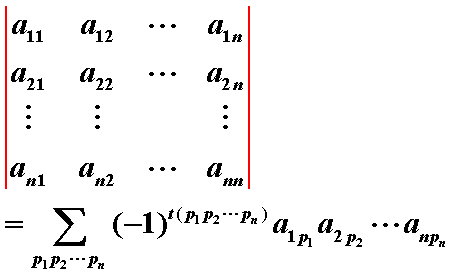
其中 t(p1,p2,...,pn)代表数列p1,p2,...,pn数列中逆序对的个数
如果t为偶数，那就加上这一项，如果t是奇数，那就减去这一项。
根据图中解释的那样，每行选取任意选取一个a[i,j]，且保证每行选取的元素不在同一列（选取的元素的j各不相同）。那么将枚举的元素乘起来，判断按照行数排列的列数数列中一共有几个逆序对来判断正负，最后将所有得到的乘积相加即可得到行列式的值。
偶对了，再提一句，行列式的行数和列数要一样才行
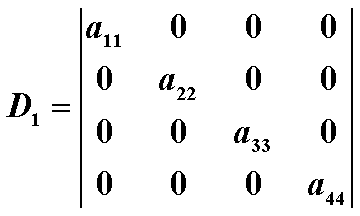
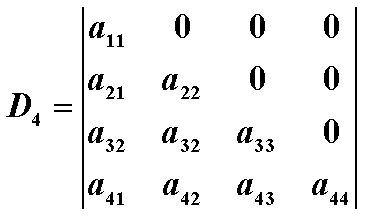
不难发现，以上这四个行列式都等于a11+a22+a33+a44，这个结论对后面的行列式转移有很大帮助
行列式的性质：
1，若我们将一个行列式D旋转90度得到新的行列式称作转置行列式（DT），那么D=DT
2、如果将行列式的两行（或两列）交换位置，那么新得到的行列式D1与原行列式D的关系为：D=-D1（交换后t的奇偶性变了）
那么得到进一步推论：推论 如果行列式有两行（列）完全相同，则此行列式为零。
3、如果行列式某一行（或列）的所有元素都乘了k，那么整个行列式的值就变成了原来的k倍。（很好证明，每次都会选取这一行的某个元素相乘，总结果就会扩大k倍，举一个例子加以证明，如下：）
通过这个结论我们也可以得出：
行列式的某一行（列）中所有元素的公因子可以提到行列式符号的外面
4、 行列式中如果有两行（列）元素成比例，则此行列式为零
证明起来也很简单，假设这两行的对应元素比值为k，由于性质3，我们可以将其中的k提出来，这样就有两行（列）是相同的，那么由性质2可以推出整个行列式的值为0
5、若行列式的某一列（行）的元素都是两数之和,则可写作两个行列式之和，例如：
，
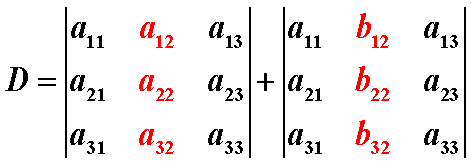
证明也很简单：
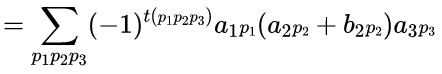
6、把行列式的某一列（行）的各元素乘以同一个倍数然后加到另一列(行)对应的元素上去，行列式不变
证明：
设：
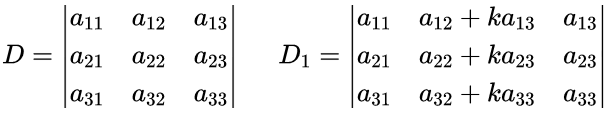
由性质5可以将D1展开：
由性质4可知：
也就是说，D1就是前面的那一项，即：
证毕
通过这些性质，我们可以将任意一个行列阵转换成上三角形式：
比如：
将第一列中的第一个作为基准，将其乘上某个数再加到其他的行中，是其他行中的第一个数都变成0，即：
交换第2行和第3行得：
将第4行加上第2行的1值，得：
现在将第3行加到第4行并将第3行*2加到第5行：
将第4行乘2加到第5行：
此时的行列式就变成了一个可以简单求解的新行列式，即：（十分抱歉，上面换行的时候忘记乘-1了，就凑合凑合看吧）
除此之外，行列式还有一种计算方法：
首先我们知道，将一个行列式展开可以得到：
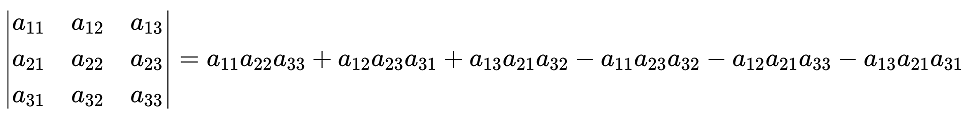
将其合并同类项，我们得到：
再将其转化成行列式得：
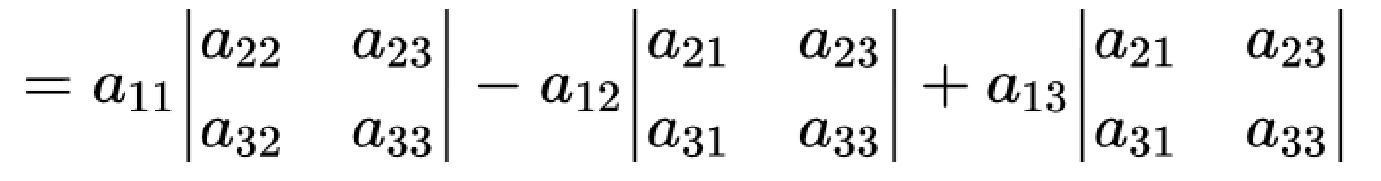
也就是说，任何一个行列式都可以用较低阶的行列式表示。
接下来引入一些概念：
1.将在n 阶行列式中，把元素 
所在的第 i 行和第 j 列划去后，留下来的n－1阶行列式叫做元素
的余子式，记作
，而将
称为元素
的代数余子式
那么我们进一步发现，在一个n阶行列式中，如果第i行（或列）除aij外其他的元素都是0，那么这个行列式就等于aij与其代数余子式Aij的乘积，即：
嘿嘿，这样的话，就可以对任意一个行列式做点什么了：
对于一个行列式，用一项将其所在的行或列上的元素全都消成0（除了他自己），再将其像刚才提到的方法降阶，即可得到低阶行列式。
想要实现这种perfect的方法，除了直接消项变成0外还可以用补0大法，举个小例子：
对于一个3*3的行列式D：
通过上文提及的行列式性质，可以将其转换成：
也就变成了：
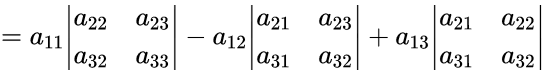
简直完美！！
下面来介绍：克拉默法则
对于一个线性方程组
如果他的系数行列式不等于0，即：
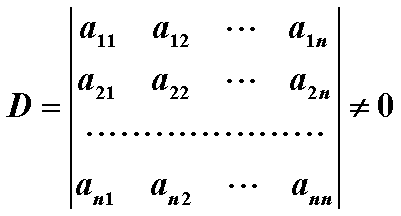
那么这个方程组的解集就是唯一的
对于解集中的任意一个解 xi，他都可以表示成：Di/D
其中Di就是将D数组的第i列换成等号右面的那一行，即
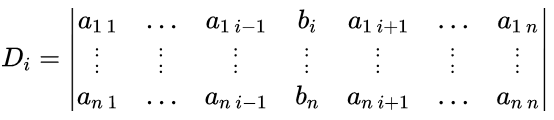
（这个竖着的省略号真难打！！）
那么，如果这个方程有无数组解或者无解，则系数行列式一定为0
接下来在介绍几个定义：
对于一个线性方程组，如果等号右边全都是0，则称这个线性方程组叫做齐次线性方程组，否则就称为非齐次线性方程组。
根据定义可知，齐次线性方程租一定有组解集全为零，我们将这组解集称作零解。
然而齐次线性方程组会不会有非零解呢？
如果齐次线性方程组的系数行列式不=0，则只有零解，没有非零解。如果齐次线性方程组有非零解,则它的系数行列式必为零！！！
终于，我们可以进入正题了！！
行列式A的各个元素的代数余子式所构成的矩阵叫做矩阵A的伴随矩阵，即A*
对于一个n阶矩阵A：
他的伴随矩阵A*就是：
注意到没？下标是不一样的！关于对角线对称！！！
下面是一条重要的性质：
那就让我来小小地证明一下吧！！
众所周知，A乘A*所得到的矩阵为：
而aiiAii不就是元素乘他的代数余子式吗？他就等于|A|，即：
现在我们构造一个新的矩阵，使得原矩阵与新矩阵完全等价：
对于其他的不在对角线上的元素，尝试构造一个与其等价的新矩阵
比如原式是a12A11+a22A21+...，构造一个b11B11+b21B21+...，这样的话b11=a12，b21=a22，也就是说有两行是相等的，那这个矩阵不就等于零？
那原矩阵就变成了：
那就等于|A|乘上一个单位矩阵，完事儿！
下面引入关于逆矩阵的概念：
对于n阶单位矩阵E和同阶方阵A，都满足：
如果存在矩阵B，使得：
那么我们说B是A的逆矩阵，记作：
如何求A的逆矩阵呢？
我们可以用刚才我们得到的结论来证明：
我们知道：
两边同时除以|A|，得：
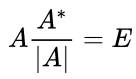
根据逆矩阵的定义，可以轻松得出：
性质：
1、
2、
3、
4、
我们进行线性变换的时候，就有了新的思路：
对于方程组：
设其系数组成的n阶方阵为A，再设：
则可以将上述线性变换记作：
变换可得：
若想要求出解集（也就是X），我们就求n阶系数方阵的逆矩阵与列矩阵Y的乘积就好
当然，求逆矩阵的方法不是唯一的！
比如：
也就是将n*2n的矩阵（先写Ann再写Enn）进行初等行变换将A变成E，此时E的位置就是A的逆。
证明如下：
寻找一个P矩阵，使得：
（1）
由于矩阵之间满足乘法结合律：
（2）
由于A经过了操作变成了E，所以：
（3）
由（2）与（3）得：
（4）
由（1）和（4）得：
即得到：
换句话说，也就是E经过操作（乘P）变成了A的逆
证毕！
总结：
求A的逆矩阵的方法：（当然还有很多，我好像都不会...）
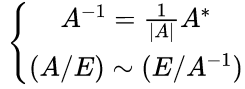
当然，想要求解一个线性方程组还还还有别的方法：就是变换增广矩阵
其实就是将方程组的系数和右侧的常数放在一个矩阵中
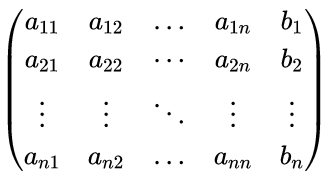
再将其转换成上三角形式，就可以对方程组进行求解了！
现在我们需要讨论方程解的存在性问题：
定义：线性方程如果有解，就称他是相容的，否则就是不相容的
对解集的三种情况进行分析：
1、相容且有无穷多解：
转换成上三角形式如下：
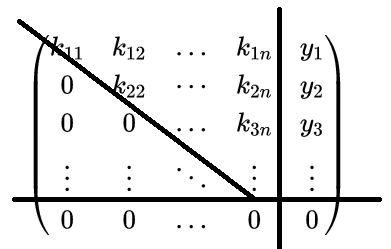
不难看出用竖线将这个矩阵隔成两部分，左部分最后一列非0元素个数（称其R(a)）和右部分y的个数（称之R(A,b)）是相等的，且大小都小于未知数个数n。
2、相容且有唯一解：
亦不难看出R(A)=R(A,b)=n
3、不相容：
亦不难看出
此时R(A)<R(A,b)
总结一下，当R(A)=R(A,b)=n时有唯一解，因为自由度和约束条件大小相等
当R(A)<R(A,b)时，显然最后0=y（y！=0）不成立，所以无解
当R(A)=R(A,b)<n时，显然自由度大于约束条件，肯定是有无穷多解的。
OK就现讲这些吧（我只会这些了。。。），会日臻完善的，祝你好运！
bye
2022/6/9
