关于倍增思想——LCA

倍增思想的应用有很多，快速幂、之前介绍的ST表等等，今天主要是谈谈关于倍增求LCA的思想以及实现

LCA，最近公共祖先，就是一棵树上的两个节点的公共的所有祖先中层数最大（即离他们最近）的祖先节点。

比如下面的这棵树中，LCA(9,12)=2，LCA(8,11)=1

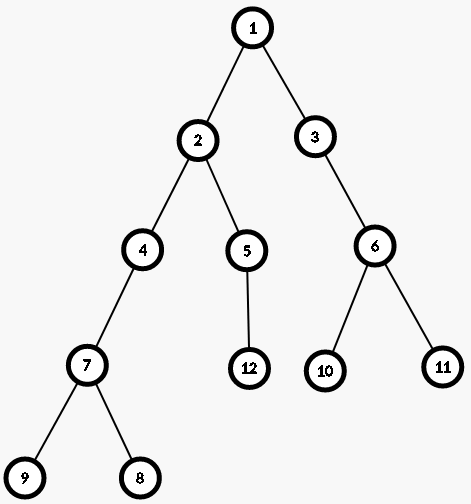
思想很简单，就是先找到比较靠下的点，让它一直往上走一直到两点处在同一层，再让两个点一直一起向上走，直到两者走到同一点，这个点就是他们的LCA

然而真的有那么简单吗？？那不免也太没有技术含量了吧！找到两个十分耗费时间的问题：

1、对于第一步将两者中的较低点一步一步向上走，非常的没必要，因为目的地是确定的，就是这个点的与另一个点齐平的祖先，直接跳到那里就行，没必要一步一步向上走。

2、对于后来两个点一起向上走的时候，如果两个点的LCA离他们特别远，一层一层地判断未免太消耗时间。尝试找到一种更优的方法：

先倍增求出LCA的具体位置，也就是从下到上倍增，如果无法满足两个点的公共祖先一样，就开始向上遍历，直到找到LCA为止

问题来了：为什么不能找到上一次满足两点祖先相同的点，再从上向下遍历呢？仔细想想，如果这么干，从父节点向下遍历子节点，如果子节点只有一个还好说，子节点万一有多个，那我怎么知道应该向下遍历哪一个子节点呢？与其这样左右为难，还不如从下向上枚举，因为每个节点有且仅有一个父节点（否则不符合社会伦理问题），能够有效避免这种尴尬的问题

关于代码实现：

 

 

#include<iostream>
#include<cstdio>

using namespace std;

const int N=5e5+10;
int nxt[N],to[N],head[N],num,deep[N],father[N][21],n,m,p,a,b,c;

void add(int _from,int _to)//加边建图 
{
    //head[i]表示以第i的点为起点的所有边中最后一条边的编号
    //nxt[i]表示上一个与边i同起点的边的编号 
    nxt[++num]=head[_from];
    to[num]=_to;
    head[_from]=num;
}

void dfs(int x)
{//father[i][j]代表以点i向上走2^j到的点 
    deep[x]=deep[father[x][0]]+1;
    for(int i=0;father[x][i];i++)
    {
        father[x][i+1]=father[father[x][i]][i];
    }   
    for(int i=head[x];i;i=nxt[i])
    {
        if(!deep[to[i]])
        {
            father[to[i]][0]=x;
            dfs(to[i]);
        }
    } 
        
}
int lca(int x,int y)
{
    if(deep[x]>deep[y])
    {
        swap(x,y);
    }
    for(int i=20;i>=0;i--)
    {
        if(deep[father[y][i]]>=deep[x])
        {
            y=father[y][i];
        }    
    } 
    if(x==y)
    {
        return y;
    } 
    for(int i=20;i>=0;i--)
    {
        if(father[y][i]!=father[x][i]){
            y=father[y][i];
            x=father[x][i];
        }
    }
    return father[x][0];
}
int main()
{
    scanf("%d%d%d",&n,&m,&p);
    for(int i=1;i<n;++i)
    {
        scanf("%d%d",&a,&b);
        add(a,b);
        add(b,a);
    }
    dfs(p);
    for(int i=1;i<=m;++i){
        scanf("%d%d",&a,&b);
        printf("%d\n",lca(a,b));
    }
    return 0;
}

 

当然，求LCA的方法除了倍增之外还有还很多种，比如：

1、线段树

2、树链剖分

3、Tarjian

由于上述难度较大（For me），我只简单的介绍思想，至于代码实现，就不是我的能力范畴之内的了：

 

 

1、线段树求法：

先介绍一下什么叫欧拉序：

就是用DFS遍历一棵树，但是回溯的时候经过的点也要加入序列，举个最简单的例子：

 

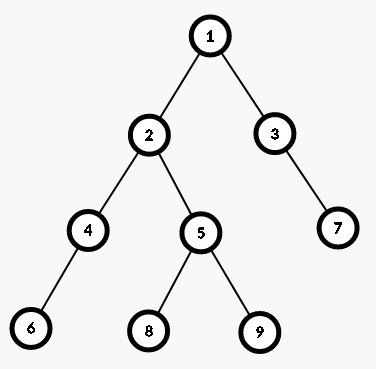
这棵树的欧拉序就是： 1 2 4 6 4 2 5 8 5 9 2 1 3 7 3 1

那我们如果想找到任意两个点的LCA，就找到这两个点在欧拉序中的位置，以他们为起点和终点的区间内就一定有他们的LCA（感性理解一下，从一个目标点出发到另一个目标点，如果两个点不在同一条线上，那一定会往上跳到出发点的一个个祖先，再向下遍历，直到遍历到另一个目标点），而且他们的LCA就是这个区间中序号最小的点（确保是在一棵保证序号严格从上到下递增的，十分抱歉的是上图好像并不遵循这样的规律，是我图画错了。。。），因为比他大的点还没有遍历到，而比它更小的点无法满足成为LCA的条件

但是还有一个小问题就是万一目标点在序列中有好几个，那我取那个点作为区间的端点呢？ 

其实取哪个都OK，因为遍历的时候一定保证两个目标点之间有相对应的LCA，

这样的话，问题就变成了：

给定一个序列，n次询问，每次给出询问区间左右端点，求这个区间的最小值。

这不就是纯裸的线段树吗？！连区间修改都不用！！

 

 

2、树链剖分：

首先介绍几个概念：

重儿子：将此节点的两个子节点作为根节点，其中两个子树节点较多的那棵对应的根节点就是重儿子

轻儿子：此节点除了重儿子之外的儿子就是轻儿子。

（一个节点的重儿子只能有一个，轻儿子可以有很多个。如果有一些儿子对应的节点数一样多，那就随便取一个当做重儿子，其他都是轻儿子）

链：起点为轻儿子或根节点，其余节点均为重儿子的边相连得到的长边

而树链剖分，就是将树所有的边划分成不同的链集

对于两个目标节点，如果他们在同一条链上，就直接返回深度较小的点。

如果他们不在同一条链上，就将编号较大的点进行更新，更新成他的父节点，直到两个点在同一条链上为止。

而代码比较难实现，在这里直接推荐我“大哥”的博客，那里有代码（虽然没有详解）

https://www.cnblogs.com/z-2-we/p/16016269.html

 

 

3、Tarjan

 

我要是想求得两个节点的LCA，先从根节点开始查找他所有的子节点，再记两个目标节点已经被访问，选取一个节点，查找所有与他有关系的祖先，若查找到的祖先已经被访问，就像上找父亲节点，直到找到的父亲节点未被访问，这个父节点就是两个节点的公共祖先。

相关大佬链接：https://www.cnblogs.com/z-2-we/p/16010245.html

 

那LCA有啥用呢？

1、求出路径从点U到点V的点权之和

　　可以设LCA（U，V）=W，d[i]表示为i到根节点的权值之和，a[i]表示点i的权值，则可以将U到V点权之和表示为：d[U]-d[W]+d[V]-d[W]+a[W]=d[U]+d[V]-2d[W]+a[W]，如图所示：

 

 

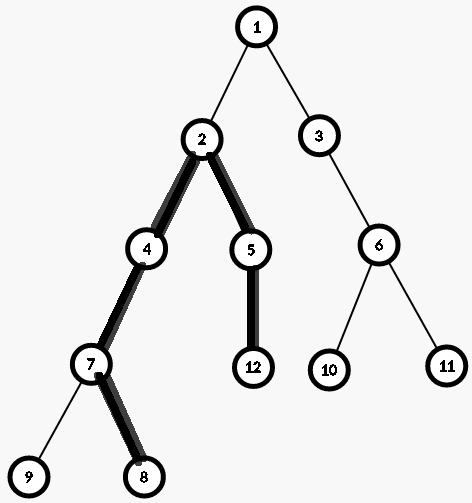
2、求一棵次小生成树

先求出最小生成树，再枚举所有的非树边，每次将其加入最小生成树中，一定能组成一个环（因为每个点最小生成树中都有），再用树上倍增求出LCA的位置，LCA以下的就是一个环了，找出这个环中除新添的那条边外的最大边，将其删除，这样就变成了一颗新树。记录新的树中边权之和，诶个遍历边每次比较树中所有边权之和找出最小值，即次小生成树。