关于组合数学基础

今天学了一些基础数论，简单记录一下：

首先是前备基础：

1.小学奥数之排列组合

排列：

 

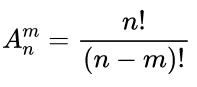
组合：

组合重要公式：

 

  

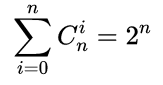
 这些显而易见的东西也不过多赘述，本质就是杨辉三角与组合还有完全多项式系数之间的关系

 

2.基础数论算法：

假设x≡y (%p)
x+a ≡ y+a (% p)
x-a ≡ y-a (% p)
x*a ≡ y*a (% p)

(a + b)%p = (a%p + b%p)%p
(a - b)%p = (a%p + b%p)%p
(a - b)%p = (a - b + p)%p
由此得知：
a*b%p = (a%p)*(b%p) %p

 

关于逆元

众所周知，在取模的意义下是不能直接作除法的。

所以引进逆元这个概念，意义是：

 

除以一个数，等于乘上这个数的逆元；

乘以一个数，等于除以这个数的逆元

所以只要求出一个式子的逆元，就可以将取模意义下的除法转化成驱魔意义下的乘法从而直接进行计算。

对于正整数a,b，如果能找到正整数x使得ax ≡ 1 (% b)，我们称x是a在模b意义下的逆元（gcd(a,b)=1时才满足，要不然还可以约分）

关于逆元的求法，我只介绍有关费马小定理的算法和线性求逆元

费马小定理应该没有人不知道吧

建立一个p的完备剩余系{1,2,3.....,p-1}，因为gcd{a,p}=1，所以{a,2a,3a,.....,(p-1)a}也是p的完备剩余系。将这两个完备剩余系分别相乘，由于其中定没有p的因数，所以有

 由于p是质数，所以得到：

  两边同时再乘p的负一次方，就得到：

 

 

线性求逆元

int[i]代表i的逆元，即

 设p=g*k+r，则g*k+r ≡ 0 (mod p)

 

由于p是质数，所以

移项得出：

 

 

 

进一步得出：

 

 

得到递推式：

 

 

(实在抱歉，本人能力有限，无法在LaTex上将‘%’打出，因此用“mod”以替之）

OK，就讲这么多，接下来步入正轨：

其实接下来的也是一些不证自明的数学推算：

 

 

 只要找到这道题的规律就好了，寻找杨辉三角与组合数位之间的关系：

不难发现：

 

不难发现，组合数与杨辉三角的每个数都是相互对应的，其实这规律也是由于组合数的性质得出的，即：

 

所以原问题就变成了暴力递推杨辉三角，找出符合条件的元素个数

但是复杂度O（n2）的确让人难以接受，因此还需要前缀和优化

代码如下：

#include<iostream>
#define ll long long
int const N=2000; 
using namespace std;
ll t,n,m,k,f[N+10][N+10],s[N+10][N+10];
int main()
{
    cin>>t>>k;
    for(int i=0;i<=N;i++)
    {
        f[i][i]=f[i][0]=1;
    }
    for(int i=1;i<=N;i++)
    {
        for(int j=1;j<i;j++)
        {
            f[i][j]=(f[i-1][j-1]+f[i-1][j])%k;
        }
    }
    for(int i=1;i<=N;i++)//直接用前缀和递推 
    {
        for(int j=1;j<=N;j++)
        {
            s[i][j]+=s[i][j-1]+s[i-1][j]-s[i-1][j-1];
            if(f[i][j]==0&&j<=i) s[i][j]++;        
        }
    } 
    for(int i=1;i<=t;i++)
    {
        ll ans=0;
        cin>>n>>m;
        cout<<s[n][m]<<endl;
    }
    return 0;
} 

 其实还有一些很明朗的性质，比如：

如果两项式的幂指数n为偶数，则中间项T（n/2+1）的系数最大，若n为奇数，则中间两项T((n+1)/2）与T((n+1)/2+1)系数最大

 

关于卢卡斯定理（Lucas' Theorem）

 

边界条件：Lucas(x,0,p)=1

简单点来说，cm指的是，

由于

所以用我们刚才讲得逆元表示的话就是：

ll c(int n,int m){
    if(m>n) return 0;
    return (num[n]*inv(num[m])%p)*inv(num[n-m])%p;
}
ll lucas(ll n,ll m){
    if(m==0) return 1;
    return lucas(n/p,m/p)*c(n%p,m%p)%p;
}

 

谢谢观看，再见