张量计算符

张量有加、减、点乘、叉乘、并乘运算

1、张量的加减：即对应的分量加减；

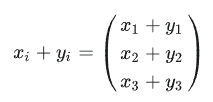
2、张量的点乘（缩并）

点乘是降阶的！

假如a有4阶，b有2阶，那么a点乘b得到的就是4-2=2阶

假如a有2阶，b有1阶，那么a点乘b得到的就是2-1=1阶（矩阵乘向量）

假如a有2阶，b有2阶，那么a点乘b得到的就是2-2=0阶（矩阵乘矩阵）

假如a有1阶，b有1阶，那么a点乘b得到的就是1-1=0阶（向量乘向量）

所以我们还明白了：点乘结果的阶数就是阶数大的减去阶数小的。

3、二阶张量的双点积

向量（也就是一阶张量）的点乘都写成一个点的点积。

而二阶张量的点乘都写成两个点的点积。如 a:b, 假如写上下标就是 a_ijb_ij

ij都是哑标，直接就加没了。所以两个2阶张量点乘的结果是0阶张量，即一个数，或者说是标量。

为什么要写两个点呢？这是因为有两个下标被爱因斯坦求和约定给求和了，同时它又是两个二阶的张量相乘，所以就写成两个点。

双点积应该很常见，因为它其实就是两个矩阵对应分量一对一的相乘。

假如写成矩阵形式的话，

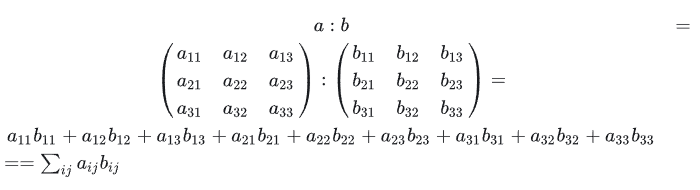
4、张量的并乘（张量积）

并乘是升阶的！

并乘结果的阶数就是阶数之和。

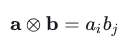
并乘除了写圈圈里面一个叉子，还可以什么都不写，就紧贴着。

ab = a_ib_j

可以想象，i和j都是自由下标，结果为2阶张量，所以这其实是9个分量

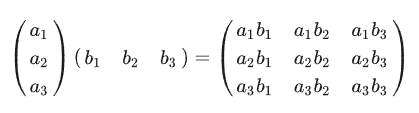
向量并乘又被称为外积(outer product)（与内积相对应）

矩阵并乘又被称为克罗内克积(kronecker product)

张量的并乘又被称为直积(direct product)，或者就叫张量积（tensor product)。

(PS 张量积这种说法比较普遍)

5、张量的叉乘

叉乘是不升不降的。

例如向量的叉乘

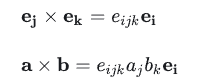
这里e_i代表坐标轴的单位向量

e_ijk叫做置换符号(又叫Racci符号）

6、克罗内克三角（函数）（Kronecker delta）

它是一个二阶张量

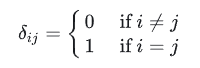
可见，它其实就是单位阵。

可用克罗内克三角来化简许多运算

他有一条很好的性质，那就是他能换下标。

比如

其实这个换了相当于没换，因为只有一个下标。假如有两个，那就有区别了

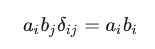
可见后面那个 \(\delta\) 把 b 的下标 j 换成了下标 i