E 走呀走

二维DP。
#include<cstdio>
#include<iostream>
#define ll long long
using namespace std;
ll a[2000][2000];
ll ans[2000][2000];
int main(){
ll n,m;
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=n;i++){
for(ll j=1;j<=m;j++){
scanf("%lld",&a[i][j]);
//第i行 第j个
}
}
ans[1][1]=a[1][1];
for(ll i=1;i<=n;i++){
for(ll j=1;j<=m;j++){
ans[i][j]=max(max(
ans[i-1][j]+a[i][j],
ans[i][j-1]+a[i][j]),
ans[i][j]);
}
}
cout<<ans[n][m]<<endl;
return 0;
}
F 关灯问题(二)

埃氏筛法。
#include<cstdio>
#include<iostream>
using namespace std;
const int MAXN=2e6;
int n;//上界
int cnt[MAXN];
void init(int val){
for(int i=1;i<=n&&i*val<=n;i++){
cnt[i*val]++;
}
}
int main(){
int m,q;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=m;i++){
init(i);
}
for(int i=1;i<=q;i++){
int val;
scanf("%d",&val);
printf("%d\n",cnt[val]);
}
return 0;
}
H 觉悟排列(Easy Version)
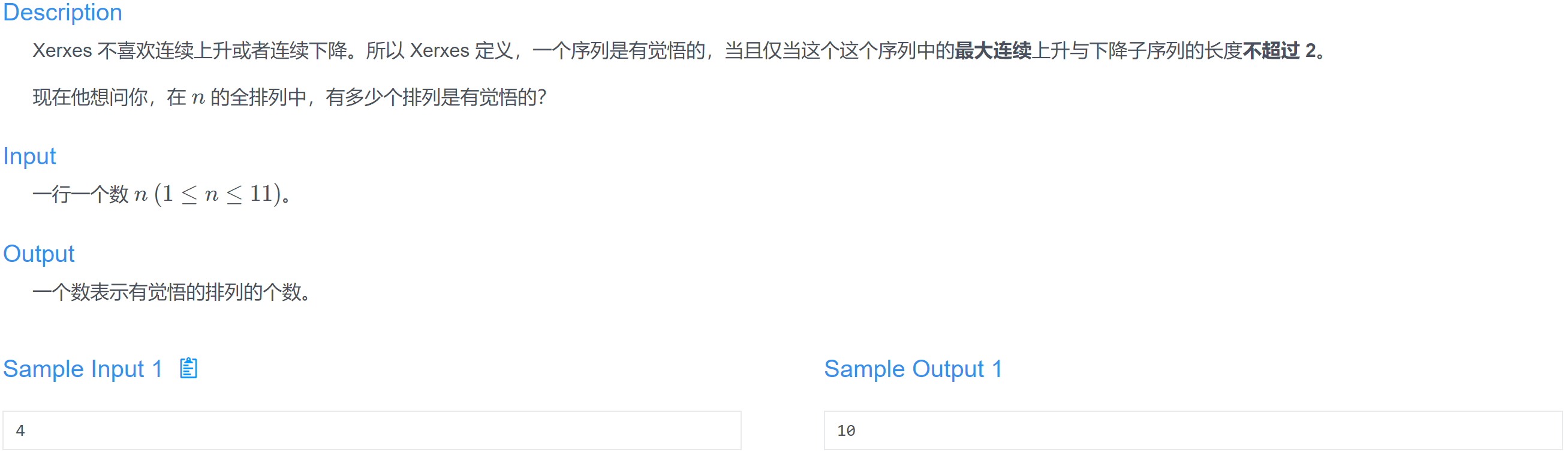
打表。暴力也可以(更简单)
J 最大公约数


观察z的式子,可以发现z=x/y,然后进行修改。总结样例,不难发现答案为x/gcd(x,y)*y/gcd(x,y)。
#include<cstdio>
#include<iostream>
#define ll long long
using namespace std;
ll gcd(ll a,ll b){
if(b>a)swap(a,b);
if(b==0)return a;
return gcd(a%b,b);
}
int main(){
ll t;
scanf("%lld",&t);
for(ll i=1;i<=t;i++){
ll x,y;
scanf("%lld%lld",&x,&y);
ll val=gcd(x,y);
ll num=(x/val)*(y/val);
cout<<num<<endl;
}
return 0;
}
l 植物大战僵尸

带修主席树。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=3e5+10;
int n,m,tot,sz,num,a[N],b[N],rt[N],s[N],sum[N*300],ls[N*300],rs[N*300],rootl[N],rootr[N],cntl,cntr;
struct node{
int l,r,k,op;
}q[N];
int get(int x){return lower_bound(b+1,b+sz+1,x)-b;}
int lowbit(int x){return x&(-x);}
struct Tree{
void update(int &o,int pre,int l,int r,int x){
o=++tot;
sum[o]=sum[pre]+1;
ls[o]=ls[pre];
rs[o]=rs[pre];
if(l==r) return;
int mid=l+r>>1;
if(x<=mid) update(ls[o],ls[pre],l,mid,x);
else update(rs[o],rs[pre],mid+1,r,x);
}
void add_update(int &o,int l,int r,int x,int val){
if(o==0) o=++tot;
sum[o]+=val;
if(l==r) return;
int mid=l+r>>1;
if(x<=mid) add_update(ls[o],l,mid,x,val);
else add_update(rs[o],mid+1,r,x,val);
}
void add_update(int k,int val){
int x=get(a[k]);int y=get(val);
a[k]=val;
while(k<=n){
add_update(s[k],1,sz,x,-1);
add_update(s[k],1,sz,y,1);
k+=lowbit(k);
}
}
int query(int last,int now,int l,int r,int x){
if(l==r) return l;
int cnt=sum[ls[now]]-sum[ls[last]];
for(int i=1;i<=cntl;++i) cnt-=sum[ls[rootl[i]]];
for(int i=1;i<=cntr;++i) cnt+=sum[ls[rootr[i]]];
int mid=l+r>>1;
if(cnt>=x){
for(int i=1;i<=cntl;++i) rootl[i]=ls[rootl[i]];
for(int i=1;i<=cntr;++i) rootr[i]=ls[rootr[i]];
return query(ls[last],ls[now],l,mid,x);
}else{
for(int i=1;i<=cntl;++i) rootl[i]=rs[rootl[i]];
for(int i=1;i<=cntr;++i) rootr[i]=rs[rootr[i]];
return query(rs[last],rs[now],mid+1,r,x-cnt);
}
}
int kth(int l,int r,int k){
cntl=cntr=0;
for(int i=l-1;i;i-=lowbit(i)) rootl[++cntl]=s[i];
for(int i=r;i;i-=lowbit(i)) rootr[++cntr]=s[i];
int ans=query(rt[l-1],rt[r],1,sz,k);
return b[ans];
}
}tr;
int main(){
scanf("%d%d",&n,&m);//n个高坚果 m个操作
for(int i=1;i<=n;++i) scanf("%d",&a[i]),b[++sz]=a[i];
for(int i=1;i<=m;++i){
int opt;
scanf("%d",&opt);//m个操作
if(opt==1){//查找
q[i].op=1;
q[i].l=1;
q[i].r=n;
scanf("%d",&q[i].k);
}else{//修改
q[i].op=2;
scanf("%d%d",&q[i].l,&q[i].r);b[++sz]=q[i].r;
}
}
sort(b+1,b+sz+1);
int num=unique(b+1,b+sz+1)-b-1;
sz=num;
for(int i=1;i<=n;++i) tr.update(rt[i],rt[i-1],1,sz,get(a[i]));
for(int i=1;i<=m;++i){
if(q[i].op==1){
printf("%d\n",tr.kth(q[i].l,q[i].r,q[i].k));
}else{
tr.add_update(q[i].l,q[i].r);
}
}
return 0;
}
Q 杠杆の套娃
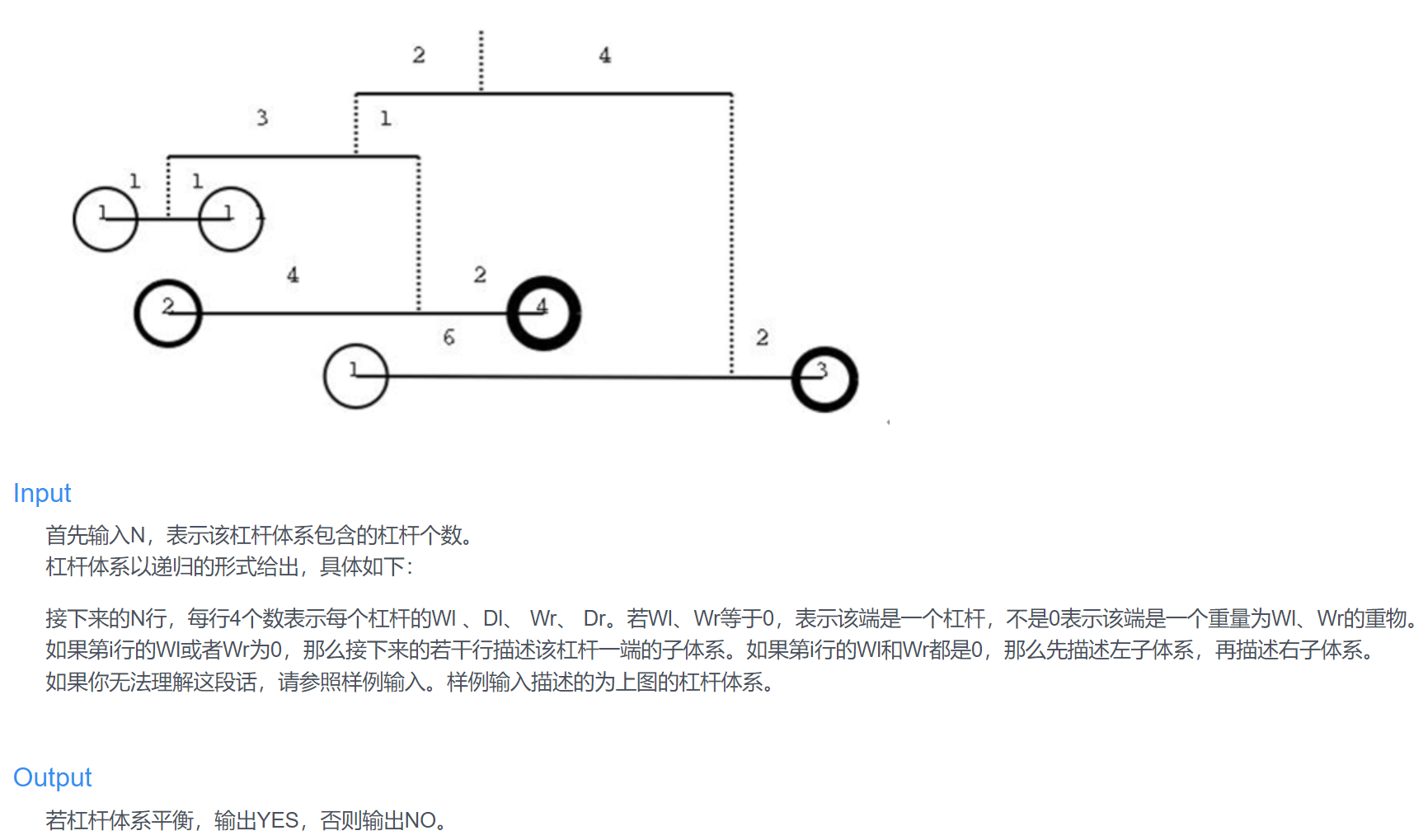
利用二叉树的性质,发现递归有着同样的性质。
#include<cstdio>
#include<iostream>
using namespace std;
bool solve(int &w){
int w1,w2,dis1,dis2;
bool canSolve1=1,canSolve2=1;//两端能否平衡
scanf("%d%d%d%d",&w1,&dis1,&w2,&dis2);//当前杠杆两端的重量
if(w1==0){
canSolve1=solve(w1);
}
if(w2==0){
canSolve2=solve(w2);
}
w=w1+w2;//总重量
return canSolve1&&canSolve2&&(w1*dis1==w2*dis2);
}
int main(){
int n;
scanf("%d",&n);
int w;
if(solve(w)){
printf("YES\n");
}else{
printf("NO\n");
}
return 0;
}



