CF830C Bamboo Partition

---

 对式子进行化简后可得

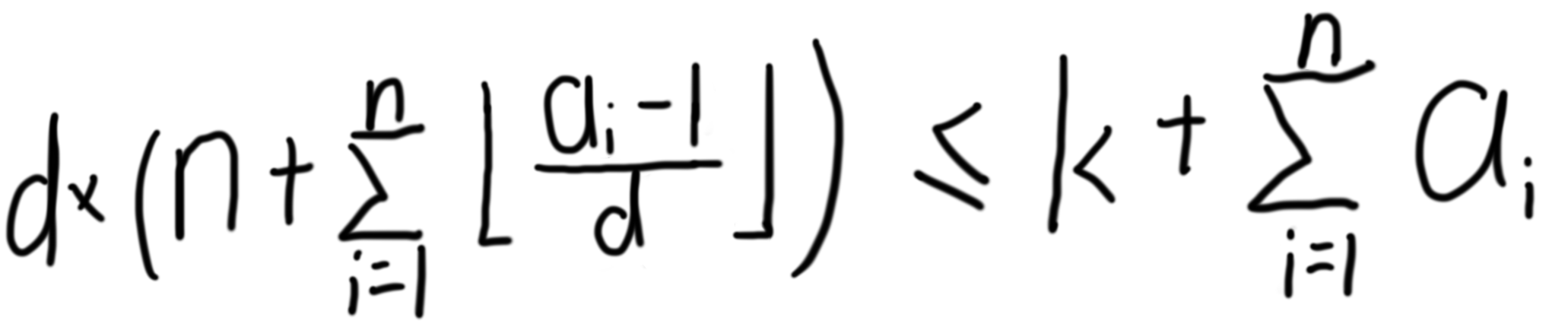
对左边的式子整体进行因式分解，可以发现d和另一个元素的值最多有一个>=sqrt(k+sigma(a_i))（可由反证法证得）

考虑到可以枚举i，范围为1--sqrt(k+sigma(a_i))，每次将d设为i和(k+sigma(a_i))/i，就可以将所有可能性全部遍历。

---

 

#include<cstdio>
#include<iostream>
#include<cmath> 
#define ll long long
using namespace std;
ll a[200],n,maxValue;

bool isOk(ll d){
	ll tmpSum=0;
	for(ll i=1;i<=n;i++){
		tmpSum+=(a[i]-1)/d;
	}
	tmpSum+=n;
	return maxValue>=(d*tmpSum);
}

int main(){
	ll k;
	scanf("%lld%lld",&n,&k);
	
	maxValue=k;
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
		maxValue+=a[i];
	}
	
	ll ans=0;
	for(ll i=1;i*i<=maxValue;i++){
		if(isOk(i))ans=max(ans,i);
		if(isOk(maxValue/i))ans=max(ans,maxValue/i);
	}
	printf("%lld\n",ans);
	return 0;
}