
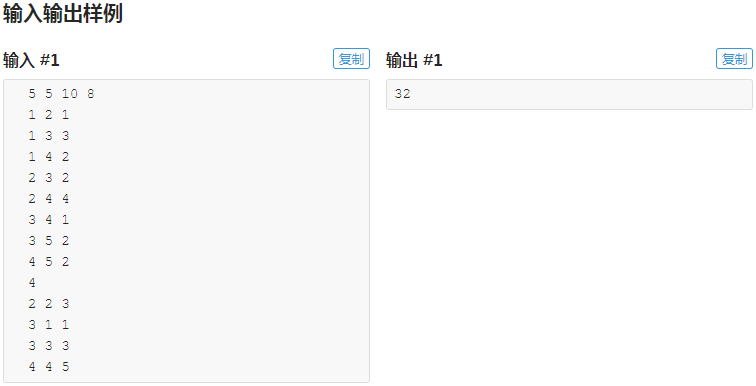
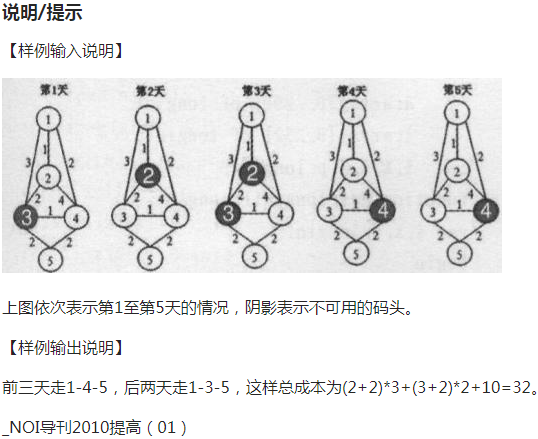
转移方程:
- dis[i][j]:时间i~j不改变线路的最短路.
- cost[i]:从第1天到第i天的最低代价.
- cost[i]=cost[j]+dis(j+1,i)*(i-j)+k(0<=j<i).
初始值:
- cost[0]=-k.
基本思路:
- 预处理dis[i][j],进行cost[]转移即可.
#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
#define ll long long
using namespace std;
const int MAXN=40,MAXM=8e2,MAXTIME=2e2;
struct Edge{
int from,to,w,nxt;
}e[MAXM];
int head[MAXN],edgeCnt=1;
void addEdge(int u,int v,int w){
e[++edgeCnt].from=u;
e[edgeCnt].to=v;
e[edgeCnt].w=w;
e[edgeCnt].nxt=head[u];
head[u]=edgeCnt;
}
struct Node{
int v,dis;
bool operator <(Node another)const{
return dis>another.dis;
}
};
int m;
int dis_dijktra[MAXN];
bool canGo[MAXN];
void dijkstra(){
memset(dis_dijktra,0x3f,sizeof(dis_dijktra));
priority_queue<Node> q;
if(canGo[1])q.push(Node{1,0});
dis_dijktra[1]=0;
while(!q.empty()){
Node nowNode=q.top();
q.pop();
int nowU=nowNode.v;
if(dis_dijktra[nowU]!=nowNode.dis)continue;
for(int i=head[nowU];i;i=e[i].nxt){
int nowV=e[i].to;
if(!canGo[nowV])continue;
if(dis_dijktra[nowV]>dis_dijktra[nowU]+e[i].w){
dis_dijktra[nowV]=dis_dijktra[nowU]+e[i].w;
q.push(Node{nowV,dis_dijktra[nowV]});
}
}
}
}
bool timeCanGo[MAXTIME][MAXN];
int getDis(int l,int r){//时间l到r的距离
memset(canGo,1,sizeof(canGo));
for(int i=1;i<=m;i++){
for(int j=l;j<=r;j++){
if(!timeCanGo[j][i])canGo[i]=0;
}
}
dijkstra();
return dis_dijktra[m];
}
ll dis[MAXTIME][MAXTIME];
int n,k;
ll cost[MAXTIME];
int main(){
int e;
scanf("%d%d%d%d",&n,&m,&k,&e);
for(int i=1;i<=e;i++){
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
addEdge(a,b,w);
addEdge(b,a,w);
}
int d;
scanf("%d",&d);
memset(timeCanGo,1,sizeof(timeCanGo));
for(int i=1;i<=d;i++){
int p,a,b;
scanf("%d%d%d",&p,&a,&b);
for(int j=a;j<=b;j++){
timeCanGo[j][p]=0;
}
}
for(int l=1;l<=n;l++){
for(int r=1;r<=n;r++){
dis[l][r]=getDis(l,r);
}
}
memset(cost,0x3f,sizeof(cost));
cost[0]=-k;
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++){
cost[i]=min(cost[i],cost[j]+dis[j+1][i]*(i-j)+k);
}
}
printf("%d\n",cost[n]);
return 0;
}


