2个长度为k的连续子序列和最大

链接：https://ac.nowcoder.com/acm/problem/15553
来源：牛客网

今天qwb要参加一个数学考试，这套试卷一共有n道题，每道题qwb能获得的分数为ai，qwb并不打算把这些题全做完，
他想选总共2k道题来做，并且期望他能获得的分数尽可能的大，他准备选2个不连续的长度为k的区间,
即[L,L+1,L+2,....,L+k-1]，[R,R+1,R+2,...,R+k-1]（R >= L+k）。

输入描述:

第一行一个整数T（T<=10）,代表有T组数据
接下来一行两个整数n,k,(2<=n<=200,000),(1<=k,2k <= n)
接下来一行n个整数a1,a2,...,an，（-100,000<=ai<=100,000）

输出描述:

输出一个整数，qwb能获得的最大分数




ans和add[],f[]因为保存和，要开浪浪
数据中有负数，一定要清数组和ans为无穷小，ans定义到里面

#include<cstdio>
#include<algorithm>
#include <cstring>
using namespace std;
const int maxn=200010;
long long add[maxn],f[maxn];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        memset(f,-0x7f,sizeof(f));
        long long ans=-1e18;
        int n,k;
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;i++)
        {
            int x;
            scanf("%d",&x);
            add[i]=add[i-1]+x;
        }
        for(int i=k;i<=n-k;i++)
        {
            f[i]=max(f[i-1],add[i]-add[i-k]);
            ans=max(f[i]+add[i+k]-add[i],ans);
            
            //printf("%d %d\n",f[i],ans);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

前缀和+dp维护第一个区间最大值，枚举第二个区间起点。

f [i] = max(f [i-1] , ai+ai-1+ai-2+...ai-k+1)

即 每引入一个新元素，新元素向前k个之和可能更新答案

---

#include<cstdio>
#include<algorithm>
#include <cstring>
using namespace std;
const int maxn=200010;
long long add[maxn],fl[maxn],fr[maxn];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        memset(fr,-0x7f,sizeof(fr));
        memset(fl,-0x7f,sizeof(fl));
        long long ans=-1e18;
        int n,k;
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;i++)
        {
            int x;
            scanf("%d",&x);
            add[i]=add[i-1]+x;
        }
        for(int i=k;i<=n-k;i++)
            fl[i]=max(fl[i-1],add[i]-add[i-k]);
        for(int i=n-k+1;i>=k+1;i--)    
            fr[i]=max(fr[i+1],add[i+k-1]-add[i-1]);
//         for(int i=k;i<=n;i++)
//             printf("%lld ",fl[i]);
//         putchar('\n');
//         for(int i=n-k+1;i>0;i--)    
//             printf("%lld ",fr[i]);
        for(int i=k;i<=n-k;i++)
            ans=max(fr[i+1]+fl[i],ans);
        printf("%lld\n",ans);
    }
    return 0;
}

 

 

 

 

 

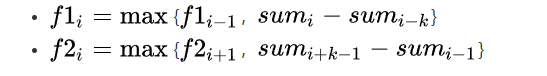
另一种做法，正反dp，最后相加，注意最后fr[i+1] + fl [i]