KMP模式匹配
KMP 模式匹配
\(\text{Update 2021.7.2}\):用 \(\rightarrow\) 代替了 \(\LaTeX\) 公式中的 \ to\ ,更新了代码中一句不必要的边界判断。
KMP 算法得名的缘由:由三位计算机科学家 \(\text{Knuth}\) ,\(\text{Morris}\),\(\text{Pratt}\) 共同设计。不是什么看毛片啦
Part 1 KMP算法可以做什么
KMP 算法,又称模式匹配算法,能够在线性时间内判定字符串 \(A_1\rightarrow A_N\) 是否为字符串 \(B_1\rightarrow B_M\) 的子串,并且求出字符串 \(A\) 在字符串 \(B\) 中各次出现的位置。
通常的 \(O(NM)\) 做法是,尝试枚举字符串 \(B\) 中的每个位置 \(i\) ,把字符串 \(A\) 与 字符串 \(B\) 的后缀 \(B_i\rightarrow B_M\) 对齐,向后扫描注意比较 \(A_1\) 与 \(B_i\) ,\(A_2\) 与 \(B_{i+1}\) ... 是否相等。我们把这种比较过程成为 \(A\) 与 \(B\) 尝试进行“匹配”。
Part 2 KMP算法原理
KMP 算法分为两步:
-
对字符串 \(A\) 进行自我“匹配”,同时求出一个数组 \(next\) ,其中 \(next_i\) 表示 “ \(A\) 中以 \(i\) 为结尾的非前缀子串”与 “ \(A\) 的前缀”能够匹配的最长长度,即:
\[next_i=max\{j\},j<i,A_{i-j+1}\rightarrow A_i=A_1\rightarrow A_j \]特别地,当 \(j\) 不存在时,令 \(next_i=0\) 。
叙述比较难懂,如图:
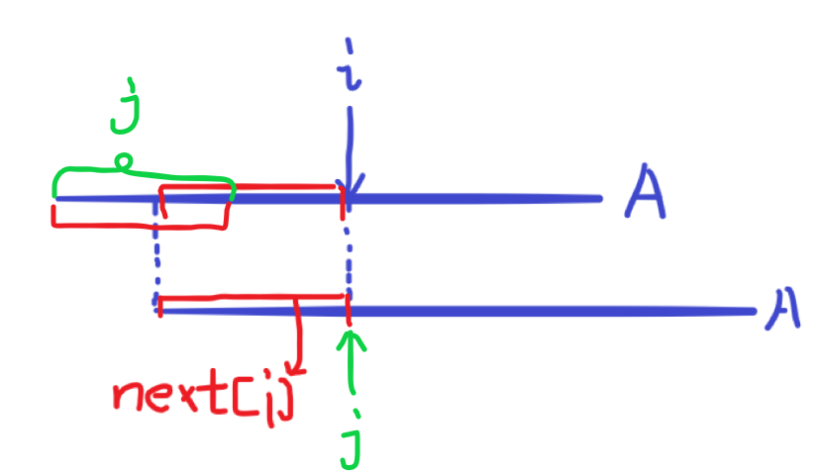
简单来说,在下面的 \(A\) 中,找到一个最大的 \(j\) ,把 \(i,j\) 对齐后使得下面的 \(A\) 串从开头到 \(j\) 和上面的 \(A\) 串从 \(i-j+1\) 到 \(i\) 完全一样。此时,三段标为红色的字符串都应该完全相同。
-
对字符串 \(A\) 与 \(B\) 进行匹配,求出一个数组 \(f\) ,其中 \(f_i\) 表示“ \(B\) 中以 \(i\) 结尾的子串”与“ \(A\) 的前缀”能够匹配的最长长度,即:
\[f_i=max\{j\},j\leq i ,B_{i-j+1}\ to\ B_i=A_1\rightarrow A_j \]步骤 2 和步骤 1 十分相似,只是把上面的字符串换成了 \(B\) 串而已,不再多做解释。
由于 \(f\) 数组和 \(next\) 数组的相似性,下面只讨论 \(next\) 数组的求法,而 \(f\) 数组可以根据相似的方法求出。根据定义,\(next_1=0\) 。接下来我们按照 \(i=2\rightarrow N\) 的顺序依次计算 \(next_i\) 。
假设 \(next_1...next_{i-1}\) 已经计算完毕,当计算 \(next_i\) 时,根据定义,我们需要找到所有满足 \(j<i\) 且 \(A_{i-j+1}\rightarrow A_i=A_1\rightarrow A_j\) 的整数 \(j\) 并取最大值。为了叙述方便,我们称满足这两个条件的 \(j\) 为 \(next_i\) 的“候选项”。
使用朴素算法计算 next 数组
朴素的做法是枚举 \(j\in [1,i-1]\) 并检查 \(A_{i-j+1}\rightarrow A_i\) 与 \(A_1\rightarrow A_j\) 是否相等。
这种算法对于每个 \(i\) 枚举了 \(i-1\) 个非前缀子串,时间复杂度约为 \(O(N^2)\) 。能否更快的求出 \(next_i\) 呢?
引理
若 \(j_0\) 是 \(next_i\) 的一个“候选项”,即 \(j_0<i\) 且 \(A_{i-j+1}\rightarrow A_i=A_1\rightarrow A_j\) ,则小于 \(j_0\) 的最大的 \(next_i\) 的“候选项”是 \(next_{j_0}\) 。换言之,\(next_{j_0}+1\rightarrow j_0-1\) 之间一定没有 \(next_i\) 的候选项。
证明:
反证法。假设存在 \(next_{j_0}<j_1<j_0\) 使得 \(j_1\) 为 \(next_i\) 的“候选项”,即 \(A_{i-j_1+1}\rightarrow A_i=A_1\rightarrow A_{j_1}\) 。
分别取 \(A_{i-j_0+1}\ to\ A_i\) 和 \(A_1\ to\ A_{j_0}\) 的后 \(j_1\) 个字符,显然也相等,即\(A_{i-j_1+1}\rightarrow A_i=A_{j_0-j_1+1}\rightarrow A_{j_0}\) 。从而 \(A_{j_0-j_1+1}\rightarrow A_{j_0}=A_1\rightarrow A_{j_1}\) ,这与 \(next_{j_0}\) 最大的性质矛盾,故假设不成立。
另一方面,\(next_{j_0}\) 显然是 \(next_i\) 的候选项。
证毕。
证明看懂需要花时间,这里放一张我自己画的图帮助理解(原谅画图能力有限):
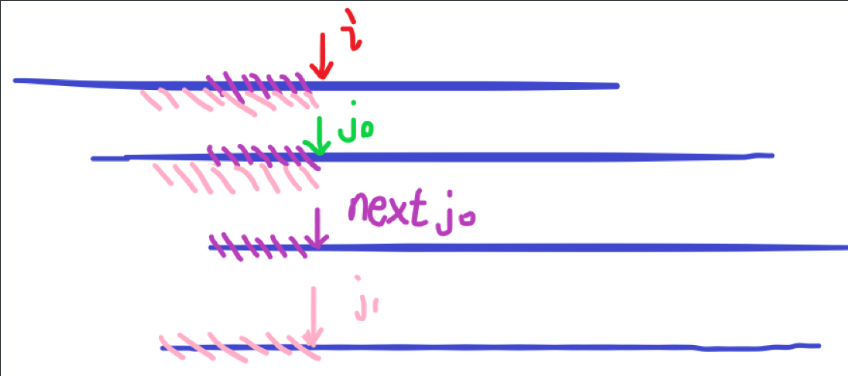
把 4 个指针都对齐,使得 \(j_0\) 为 \(next_i\) 的候选项,根据 \(next\) 数组的定义,图中划紫色斜线的部位一定相同,也就有了证明中最后一句的“另一方面,\(next_{j_0}\) 显然是 \(next_i\) 的候选项”。
现在假设出现 \(j_1\) ,且 \(next_{j_0}<j_1<j_0\) (如图),如果 \(j_1\) 为 \(next_i\) 的候选项,根据 \(next\) 数组的定义,那么图中划粉色斜线的部位一定相等,那么 \(next_{j_0}\) 的值应该为 \(j_1\) ,而不是 \(next_{j_0}\) (粉色显然长度比紫色长),这与 \(next\) 数组的“最长”定义相违背,所以 \(j_1\) 一定不存在。
Part 3 使用以上定理优化求解 next 数组
根据引理,当 \(next_{i-1}\) 计算完毕时,我们可以得知 \(next_{i-1}\) 的所有候选项,从大到小依次为:(这里用 LaTeX 不太方便,于是用代码块给出)
next[i-1],next[next[i-1]],next[next[next[i-1]]]...
另外,如果一个整数 \(j\) 是 \(next_i\) 的候选项,那么很显然 \(j-1\) 也应该是 \(next_{i-1}\) 的候选项(整体前移一位)。因此,在计算 \(next_i\) 的时候,候选项从大到小依次为:
next[i-1]+1,next[next[i-1]]+1,next[next[next[i-1]]]+1...
像下面,就是求解 \(next_8\) 的全过程:
1 2 3 4 5 6 7 8 9
i
A = a b a b a b a|a c
a b a b a|b a a c Fail(next[7]=5)
a b a|b a b a a c Fail(next[5]=3)
a|b a b a b a a c Fail(next[3]=1)
|a b a b a b a a c next[1]=0,A[1]==A[8],next[8]=1
j j+1
可以看到,我们从长到短尝试把 8 前面的字符匹配上( | 符号之前的元素),但是 8 这一位始终不能匹配。于是到最后,只能找到 \(A_8=A_1\) ,故 \(next_8=1\) 。
当然,如果在找完 next[i-1],next[next[i-1]],next[next[next[i-1]]]... 之前已经匹配上了,那么 \(next_i\) 就是匹配上的那个 \(next\) 值 \(+1\) ,这里不再赘述。
这里因为 \(j\) 始终非负,所以 \(j\) 的变化次数不会超过模式串的长度,故总复杂度 \(O(N+M)\) 。
Part 4 KMP 代码实现
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
//using namespace std;
const int maxn=1000005;
int next[maxn],f[maxn];
char A[maxn],B[maxn];//A为原串,B为匹配串
int n,m;
inline void Init(){
scanf("%s %s",A+1,B+1);
n=std::strlen(A+1),m=std::strlen(B+1);
}
inline void KMP(){
next[1]=0;//定义,next[1]=0
for(int i=2,j=0;i<=m;++i){//j表示next[i-1]
while(j>0 && B[i]!=B[j+1]) j=next[j];//next[i-1]+1先尝试匹配,然后依次变为next[next[i-1]]...
if(B[i]==B[j+1]) j++;//下一个字符相等,匹配长度++
next[i]=j;
}
for(int i=1,j=0;i<=n;++i){
while(j>0 && A[i]!=B[j+1]) j=next[j];//同next数组求解f
if(A[i]==B[j+1]) j++;
f[i]=j;
if(f[i]==m) printf("%d\n",i-m+1);//这说明在A串中找到了B串,输出开头位置
}
}
int main(){
Init();
KMP();
return 0;
}
本博客部分证明参考《算法竞赛进阶指南》,作者李煜东,特此注明。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号