人类分块精华(二)
人类分块精华(二)
优雅,永不过时。
艺术的暴力,暴力的艺术——分块。
Part 1 问题引入
在很久很久以前,程序设计师们遇到了这样一个问题。
对于一个长度为 \(n(n\leq 2e5)\) 的数组 \(A\) 有以下几种操作一共 \(m(m\leq 2e5)\) 次 :
- $ \text{Insert}$ :给定一个坐标 \(p\) ,在 \(A_p\) 后面插入一个数 \(x\) 。
- \(\text{Delete}\):给定一个坐标 \(p\) ,删除 \(A_p\) 。
- \(\text{Query}\):给定一个坐标 \(p\) ,询问 \(A_p\) 的值 。
时空限制:1s,128 MB 。
很显然又是一道毒瘤数据结构题。
看到在数组中快速插入、删除,你可能会想到链表。
但是链表不支持随机访问元素,这时 3 操作对于程序就有毁天灭地的效果。极限情况下程序复杂度达到了 \(O(mn)\) 级别,在 1s 之内显然无法完成任务。
那么数组直接模拟?显然也不行,大量的插入删除操作让你不得不移动整个数组的元素来维护下标,极限复杂度也达到了 \(O(mn)\) 级别,无法完成任务。
那么有没有办法让这两种操作的复杂度均衡一下呢?
Part 2 均衡的链表
当然是有解决办法的,谈到如何均衡链表的复杂度,先来看看链表和数组的两种操作。
众所周知,链表支持以下操作:
- \(O(1)\) 插入、删除。
- \(O(n)\) 访问单个元素。
链表的优势在于插入删除,但它使用内存不连续,故不支持随机访问,因而访问速度较慢,为\(O(n)\)。
与链表相对应的,来看看常用的数组:
- \(O(n)\) 插入、删除。
- \(O(1)\) 访问单个元素。
数组的优势体现在访问上,但因为要维护内存连续性,所以插入删除相对慢了一些,为\(O(n)\)。
今天介绍一种神奇的数据结构:块状链表。
什么是块状链表?
很简单的,字面意思,块状链表的意思就是链表套分块,像下图一样:
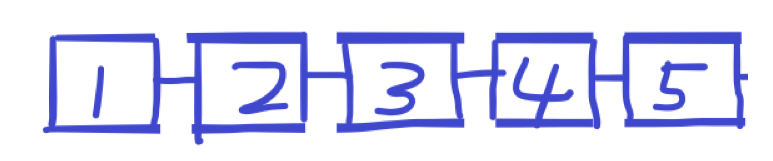
这是一个双向链表,唯一不同的是:它的每一个元素都是一个数组,而这个数组中的元素个数就是块长。
换一种说法就是先分块,分完块之后用链表的方式来链接相邻块。
来看看这样操作后的插入、删除、询问元素的时间复杂度吧:
- 先来看 \(\text{Query}\) 操作。从第一块开始遍历整个块状链表,每次检查 \(p\) 的剩余值,如果剩余值大于当前块块长,那么
p-=lenth,跳到下一个块的开始。直到 \(p\) 小于当前块块长,说明该元素在当前块内,遍历块内数组找到该元素,输出即可。这样每一次跳跃 \(\sqrt n\) 个元素寻找,最坏情况下跳 \(\sqrt n\) 次一定能找到元素所在块,所以总复杂度约为 \(O(\sqrt n)\) ,最坏情况下常数为 2 。 - 再来看 \(\text{Delete}\) 操作。和 \(\text{Query}\) 操作相同的方法,找到要删除的元素。直接删除它,然后把这个元素所在块内并且排在这个元素后面的所有元素前移一位,同时
lenth--。复杂度同上为 \(\sqrt n\) ,最坏常数为 2 。 - \(\text{Insert}\) :同 \(\text{Delete}\) ,找到元素之后把当前块内排在该元素后面的元素后移一位,然后插入,同时
lenth++。复杂度同上为 \(\sqrt n\) ,最坏常数为 2 。
这样我们就获得了一个单次插入、删除单个元素,询问单个元素复杂度为 \(O(\sqrt n)\) 的数据结构。
维护你的块状链表
如果用块状链表解决文章开头的问题,总复杂度似乎为 \(O(m\sqrt n)\) ,完全可以满足需求。
然而事实并非如此!
假设在 \(k\) 次插入之后,某一个块的长度变成了 \(L(L>>\sqrt n)\) ,也就是这个块非常长,长度远远大于我们设定的原始分块长度(有时候甚至可能爆掉块内数组)。那么假设现在有一次查询操作且 \(A_p\) 在这个超长块内,那么我们以 \(O(\sqrt n)\) 的复杂度跳到这个块之后势必要暴力遍历这个超长块,复杂度为 \(O(L)\) 而不是我们所希望的 \(O(\sqrt n)\) 。此时为了保证块长正常,需要分裂这个超长块,如下图:
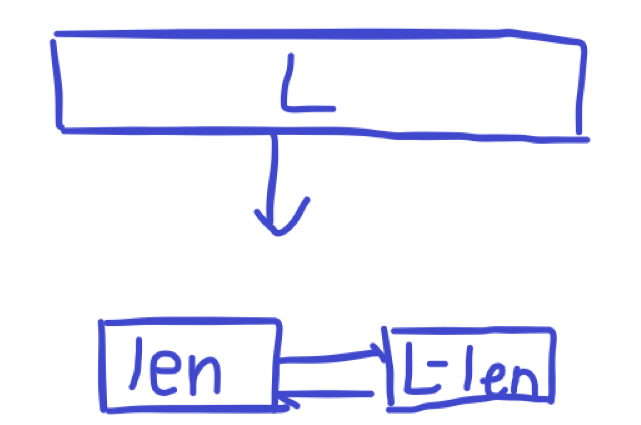
实际上就是在超长块之后新建一个块,然后把一部分元素挪到新建块里就好,建议在块长超过 2 倍设定长度的时候就进行分裂。实际操作相当于在链表中插入节点,然后复制元素即可,复杂度 \(O(\sqrt n)\) 。(我习惯于前段长度为分块设定长度,后段长度为 \(L-len\) )
还有一种情况:假设在进行 \(k\) 次删除之后,出现了一些长度非常小的块,这样我们在整块跳跃寻找 \(A_p\) 时,每次跳过的就不是我们希望的 \(\sqrt n\) 个元素,而是接近小常数个。这样查找元素复杂度会退化到接近 \(O(n)\) ,此时需要合并两个小长度块,使其长度接近 \(\sqrt n\) ,以保证时间复杂度正确,如下图:
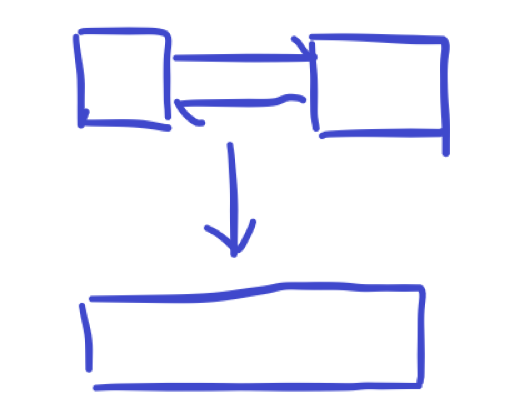
实际上就是把后面短块的元素复制到前面短块内,然后直接删除后面的短块。建议在两个块块长之和小于 \(\sqrt n\) 时就进行合并。复制块内元素,总复杂度 \(O(\sqrt n)\) 。
在正常插入删除的同时,在适当时机合并、分裂异常块,才能保证时间复杂度正确,为 \(O(m\sqrt n)\) 。
多元素插入删除
显然每次只能插入一个元素的数据结构十分鸡肋,程序设计师们想一次性插入、删除 \(k\) 个元素。
-
\(\text{Ex-Insert}\)
如果一次就把所有元素直接扔到指定位置之后,显然会导致上面所说的“超长块”的形成。如果这时候再去分裂它,白白损失了 \(O(\sqrt n)\) 的复杂度,十分不合算(直接插入也可能爆掉块内数组)。
考虑块状链表链表的性质,它支持 \(O(1)\) 在某一个整块后插入另一个整块。那么可以新建一些块,把要插入的元素都放在这些新建块里,然后整块整块 \(O(1)\) 插入。
但是要插入的位置不一定正好在某一块的末尾,那怎么办?分裂啊!在指定位置后面分裂指定位置所在块,然后在所在块后面整块插入就 OK 了。如下图:
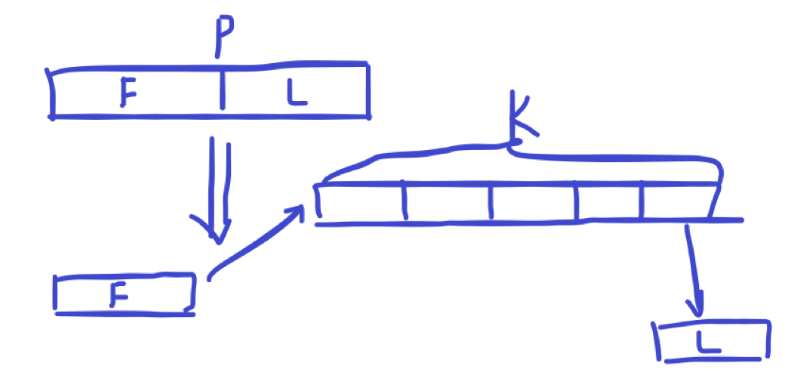
由于最后一段的长度可能很小,所以插入的最后要注意合并。
-
\(\text{Ex-Delete}\)
删除比较简单,分两种情况讨论。如果指定位置后有大于 \(k\) 个元素,直接暴力删除。否则,先直接删除指定位置后的当前块所有元素,然后整块删除。最后不足一整块的单独暴力删除,或者分裂后再整块删除。如图:

这类似于分块的“零散段暴力、整段维护思想”,另外,删除后也要注意合并。
Part 3 例题
令我没有想到的是 NOI 2003 出过一个这么简单暴力的数据结构板子题。
NOI 2003 文本编辑器
题目中的几种函数操作上面都提到过,唯一不同的是它要维护一个光标位置。这也很简单,就是我们前面讲的整块跳跃,零散块暴力的方法,找到更新光标位置即可。
代码:
#include<bits/stdc++.h>
using namespace std;
char xch,xB[1<<15],*xS=xB,*xTT=xB;//超级快读
#define getc() (xS==xTT&&(xTT=(xS=xB)+fread(xB,1,1<<15,stdin),xS==xTT)?0:*xS++)
inline int read()
{
int x=0,f=1;char ch=getc();
while(ch<'0'|ch>'9'){if(ch=='-')f=-1;ch=getc();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
return x*f;
}
int t,cursor,now,tot,len=466;
struct Node{
int pre,nxt;
int lenth;
char a[2005];
}Block[8005];
int Trashcan[100005],top,used;
inline void clear(const int id){//回收被清除的块
Trashcan[++top]=id;
memset(Block[id].a,0,sizeof Block[id].a);
Block[id].nxt=Block[id].pre=Block[id].lenth=0;
}
inline void Block_delete(const int id){//删除编号为id的块
int Nxt=Block[id].nxt;
int Pre=Block[id].pre;
Block[Pre].nxt=Nxt;
Block[Nxt].pre=Pre;
clear(id);
}
inline void Block_insert(int id){//在id后面创建一个空块
int ip;
if(used<top) ip=Trashcan[++used];
else ip=++tot;
Block[ip].nxt=Block[id].nxt;
Block[Block[ip].nxt].pre=ip;
Block[ip].pre=id;
Block[id].nxt=ip;
}
inline void split(const int id,const int pos){//分裂编号为id的块,第一段为pos,第二段为lenth-pos
Block_insert(id);
int ip=Block[id].nxt;
for(int i=pos+1;i<=Block[id].lenth;++i)
Block[ip].a[i-pos]=Block[id].a[i];
Block[ip].lenth=Block[id].lenth-pos;
Block[id].lenth=pos;
}
inline void merge(const int id){//合并编号为id和它后面的块
int ip=Block[id].nxt;
for(int i=1,j=Block[id].lenth+1;i<=Block[ip].lenth;++i,++j)
Block[id].a[j]=Block[ip].a[i];
Block[id].lenth+=Block[ip].lenth;
Block[id].nxt=Block[ip].nxt;
Block[Block[ip].nxt].pre=id;
clear(ip);
}
inline void Move(int n){
if(n==0) now=0,cursor=0;
else{
now=Block[0].nxt,cursor=0;
while(n>Block[now].lenth){
n-=Block[now].lenth;
now=Block[now].nxt;
}
cursor=n;
}
}
char str[2000005];
inline void Insert(const int n){//插入一个n的串
if(cursor==0 && now==0){
Block_insert(0);
now=Block[0].nxt;
}
if(Block[now].lenth+n<=len){
for(int i=Block[now].lenth;i>=cursor+1;--i)
Block[now].a[i+n]=Block[now].a[i];
for(int i=cursor+1,j=1;j<=n;++i,++j)
Block[now].a[i]=str[j];
Block[now].lenth+=n;
}else{
int iterator=0,k=n,Nxt;
if(cursor>=1){
split(now,cursor);
Nxt=now;
}else Nxt=0;
while(k>len){
k-=len;
Block_insert(Nxt);
Nxt=Block[Nxt].nxt;
for(int i=1;i<=len;++i)
Block[Nxt].a[i]=str[++iterator];
Block[Nxt].lenth=len;
}
if(k>=1){
Block_insert(Nxt);
Nxt=Block[Nxt].nxt;
for(int i=1;i<=k;i++)
Block[Nxt].a[i]=str[++iterator];
Block[Nxt].lenth=k;
if(Block[Nxt].lenth+Block[Block[Nxt].nxt].lenth<=len && Block[Nxt].nxt) merge(Nxt);
}
}
}
inline void Delete(int n){
if(cursor+n<=Block[now].lenth){
for(int i=cursor+1;i<=Block[now].lenth-n;++i)
Block[now].a[i]=Block[now].a[i+n];
Block[now].lenth-=n;
}else{
int k=n-(Block[now].lenth-cursor);
int Nxt=Block[now].nxt;
Block[now].lenth=cursor;//先把这一段后面的元素都删除
while(k>Block[Nxt].lenth){
int Del=Nxt;
k-=Block[Del].lenth;
Nxt=Block[Del].nxt;
Block_delete(Del);
//整块删除
}
Block[Nxt].lenth-=k;
for(int i=1;i<=Block[Nxt].lenth && k>=1;++i)
Block[Nxt].a[i]=Block[Nxt].a[i+k];
}
if(Block[now].lenth+Block[Block[now].nxt].lenth<=len && Block[now].nxt)
merge(now);
}
inline void Get(const int n){
if(cursor+n<=Block[now].lenth)
for(int i=cursor+1,j=1;j<=n;++i,++j)
putchar(Block[now].a[i]);
else{
int k=n-(Block[now].lenth-cursor);
int Nxt=Block[now].nxt;
for(int i=cursor+1;i<=Block[now].lenth;++i)
putchar(Block[now].a[i]);//先输出左段的
while(k>Block[Nxt].lenth){//整段输出
for(int i=1;i<=Block[Nxt].lenth;++i)
putchar(Block[Nxt].a[i]);
k-=Block[Nxt].lenth;
Nxt=Block[Nxt].nxt;
}
for(int i=1;i<=k;++i)//输出右段的
putchar(Block[Nxt].a[i]);
}
putchar('\n');
}
inline void Prev(){
if(cursor-1>=1) cursor--;
else{
now=Block[now].pre;
cursor=Block[now].lenth;
}
}
inline void Next(){
if(cursor+1<=Block[now].lenth) cursor++;
else{
now=Block[now].nxt;
cursor=1;
}
}
inline char opt(){
char c=getc();
while(c!='M'&&c!='I'&&c!='D'&&c!='G'&&c!='P'&&c!='N') c=getc();
return c;
}
inline void Solve(){
t=read();
while(t--){
char ch=opt();
switch(ch){
case 'M':Move(read());break;
case 'I':{
int tmp=read();
for(int i=1;i<=tmp;++i){
str[i]=getc();
if(str[i]<32 || str[i]>126)
--i;
}
Insert(tmp);
break;
}
case 'D':Delete(read());break;
case 'G':Get(read());break;
case 'P':Prev();break;
case 'N':Next();break;
}
}
}
signed main(){
Solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号