算法基础1.6位运算

前言

位运算这东西其实我一直都是能避免就避免，但是前一段时间老师上课突然讲了一个位运算的用法，而今天刚好又在算法课上学到了位运算（算法课上没有深究，只是讲了两个用法），所以我想着干脆直接借着这次机会把这方面搞得全面一点一劳永逸得了，所以我查了大量的资料，也大概总结出来了一些知识。

这篇文章将不再依托于课上所讲的东西，文章内容基本都是我自己总结得到的，算法课上讲的两个用法我会总结到位运算用法的部分里面

常见的用法其实用语言都不是很好解释，所以我基本都是自己做的图片，快累死我了。ProcessOn真是个好网站，让免费在线作图。

正文

基础知识

• & 按位与

  • 如果两个相应的二进制位都为1，则该位的结果值为1，否则为0

• | 按位或

  • 两个相应的二进制位中只要有一个为1，该位的结果值为1

• ^ 按位异或

  • 若参加运算的两个二进制位值相同则为0，否则为1

• ~ 取反

  • ~是一元运算符，用来对一个二进制数按位取反，即将0变1，将1变成0

• << 左移

  • 用来将一个数的各二进制位全部左移n位，低位以0补充，高位越界后舍弃。
  • 左移一位相当于乘2，但是要保证左移的过程中不会导致符号位发生改变

• >> 右移

  • 将一个数的各二进制位右移N位，移到右端的低位被舍弃，高位以符号位填充
  • 右移一位相当于整除2，向下取整，（-3）>> 1 = -2 ,3 >> 1 = 1
  • C++中使用/2为整除2，向0取整， （-3）/ 2 = -1，3 / 2 = 1
  • 这个在竞赛里挺常用的，虽然目前来说右移带来的时间效益微乎其微，但是似乎已经成为了一种习惯。快排，归并中求中间值一般都是直接用右移
  • 8+9 >> 1是先运算加法，因为加法有限度比位移要高

优先级：

常见用法

先把y总讲的两个写下来

1. 求n二进制下的第k位

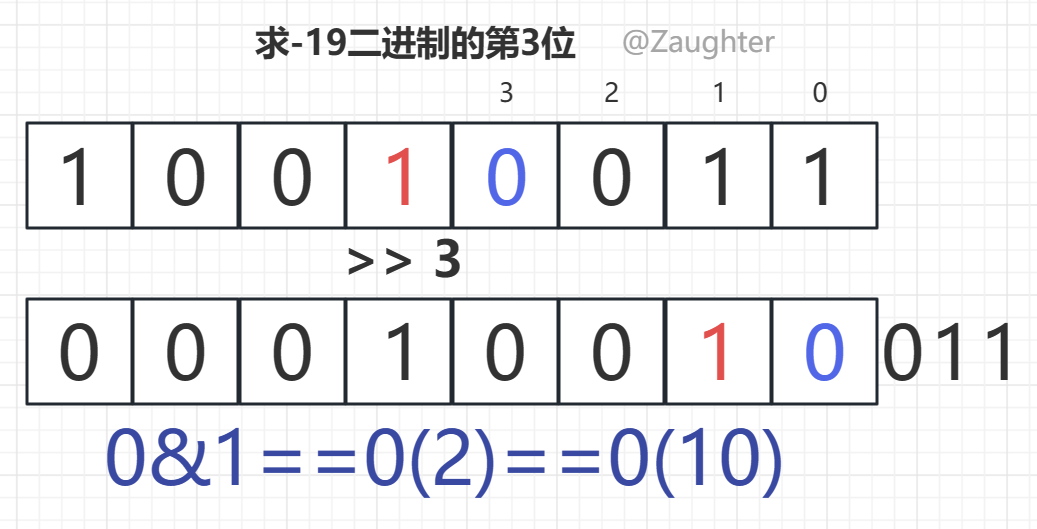
使用(n >> k) & 1，注意，对于二进制来说，个位为第0位

我们先让二进制数右移k位，这样就能让原本第k位的数移动到第0位（也就是个位），然后让他与1进行按位与的操作。注意这里的1是十进制，转换为二进制为000....01，前面的0会让n的除了个位数的其他位都变成0，只有个位有判断的必要。如果个位为1，与1进行与运算就是1，反之为0 。而这两个结果转换为十进制后数值不变，所以刚刚好

2. 返回x的最后一位1

这个方法俗称lowbit

使用x & (~x+1)，这个~x+1就相当于是-x，~将符号位也进行了取反，其实就是先将x的符号位取反变成-x的反码形式，然后再对其他位进行取反并且+1，后面的这部操作就是计算-x补码的过程，而程序中-x用的就是补码。

这个原理可以通过一个例子就能解释的很清楚：

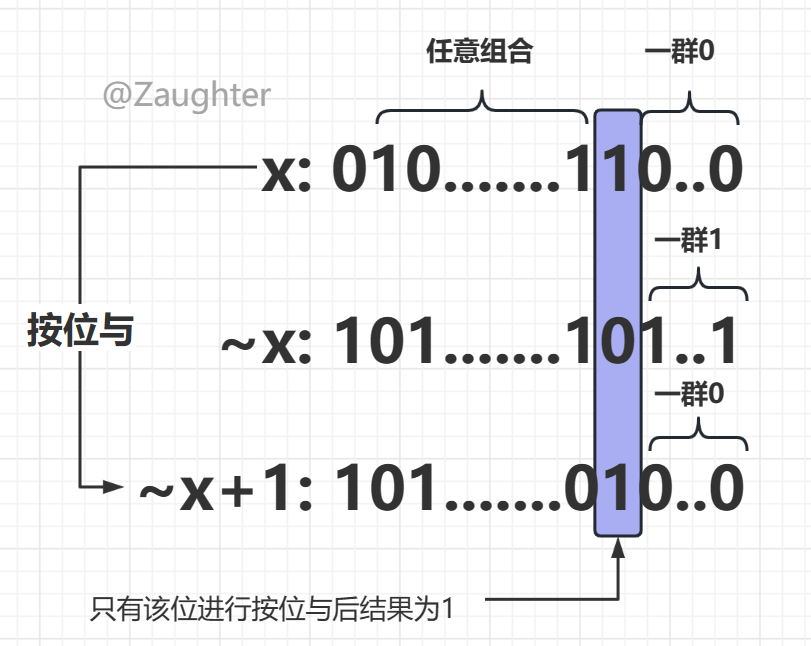
这里输出结果就是100...0这一串的十进制

这里有一道题可以用到lowbit

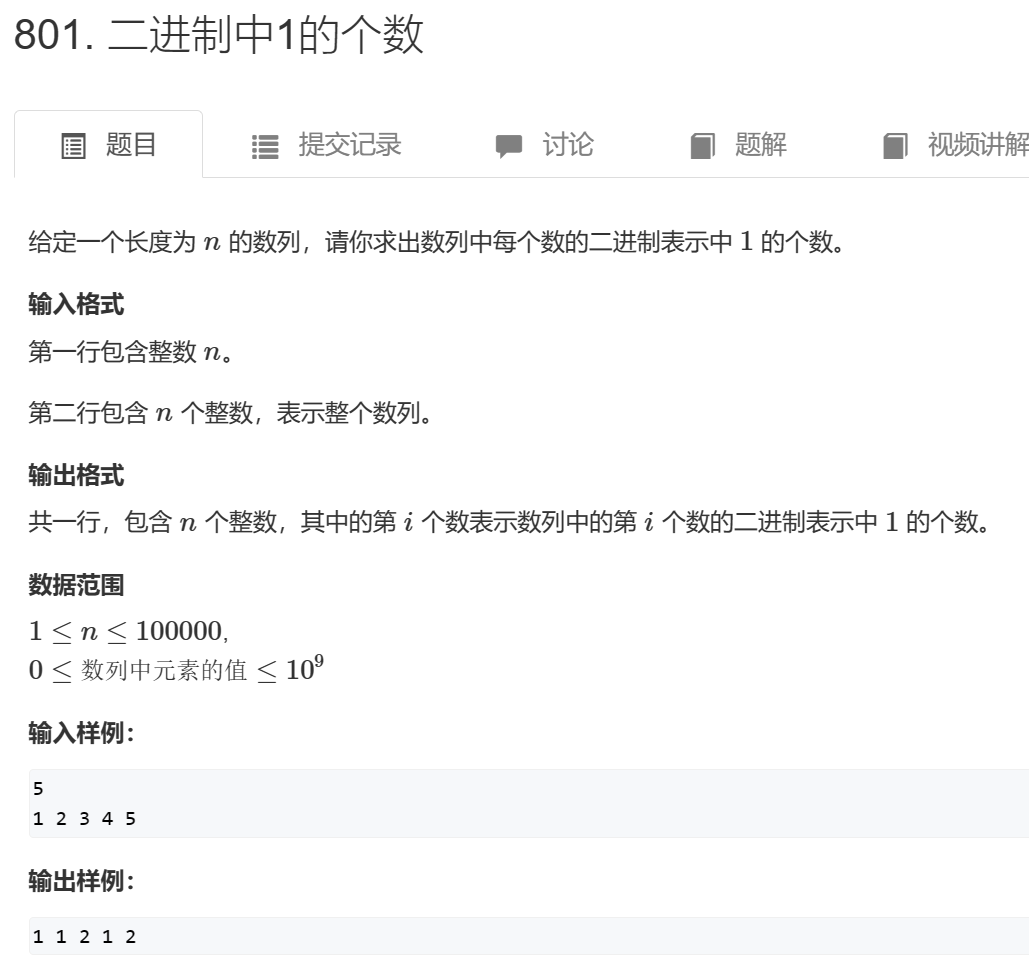
代码如下：

#include <iostream>

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);
    // 遍历数组中每一个数
    while (n -- )
    {
        int x, s = 0;
        scanf("%d", &x);
		// 这里其实相当于一个while了，只不过y总这样写能把一条语句扔到for的条件句中
        // 当i为0时这个for结束
        // 每次都会减去一串10..0，而i其实就是10..0这种串组成的一个二进制数（可能前面还有几个0）
        // 所以最后会把i减成0000000，十进制就是0
        // 每次减去一串，s就加1，因为每一串里面都有一个1，所以减了多少串就有多少个1
        for (int i = x; i; i -= i & -i) s ++ ;

        printf("%d ", s);
    }
    return 0;
}

3.交换两个变量的值

正常的方法就是新建一个临时变量，然后形成三角关系相互传递值。

而使用位运算则可以不创建这个临时变量，通过下面三行代码来实现

a = a ^ b;
b = a ^ b;
a = a ^ b;

我们首先要明确几个公式，可自行推导

这里再说一下异或运算的含义：若参加运算的两个二进制位值相同则为0，否则为1

• 任意一个变量X与其自身进行异或运算，结果为0，即X^X=0
• 任意一个变量X与0进行异或运算，结果不变，即X^0=X
• 异或运算具有可结合性，即 a ^ b ^ c = (a ^ b) ^ c = a ^ (b ^ c)
• 异或运算具有可交换性，即a ^ b = b ^ a

现在来一步一步分析

1. a = a ^ b;，这一步我们不需要实际知道a变成了多少（一个没有任何规律的十进制数），只需要知道目前a代表了a ^ b这个集合就行
2. b = a ^ b;，现在我们把a展开：b = a ^ b = a ^ b ^ b = a ^ (b ^ b) = a ^ 0 = a，这里用到了结合律，然后再用公式1得知b ^ b =0，公式2得出最后结果
3. a = a ^ b;，仍然展开，注意b的值也变了：a = a ^ b = a ^ b ^ a = a ^ a ^ b = 0 ^ b = b

交换完毕。

4.判断奇偶性

先复习一下小学知识点：

• 奇 + 奇 = 偶
• 偶 + 偶 = 偶
• 奇 + 偶 = 奇

我们再想一下二进制转十进制的方法：2 ^ (x - 1) * x ，其中x >= 1，代表位数。

所以除去第一位，后面的都是2 ^ n（n >= 1），都是偶数。只有第一位是2 ^ 0 * x，结果可能是1（奇数）或者0（偶数）

因此我们只需要判断第一位即可，余下位转化为十进制后的和一定是偶数。

• 如果第一位为0，第一位转换结果为0，偶 + 偶 = 偶
• 如果第一位为1，第一位转换结果为1，偶 + 奇 = 奇

代码如下：

if(n&1){    //若n&1==1(为真)
   //n是奇数
}
if(!(n&1)){ //若n&1!=1(为假)
  //n是偶数
}

这里的十进制1就是二进制的00000001，所以其他的结果都是0，只有个位有判断按位与结果的必要。

5.求a的b次方

这里用到了数论的知识，但是但从过程中我们也可以理解其中的含义

假如我们要求a的13次方，那么也就是b = 13，而b的二进制为1101。

那么a ^ 1101 = a ^ 0001 * a ^ 0100 * a ^ 1000，该步涉及到未学过的知识，我们暂认为公理

也就是说a ^ 13 = a ^ 1 * a ^ 4 * a ^ 8，这样其实是可以理解的

• 这个思路的时间复杂度为O(logn)，比库函数pow的O(n)要快
  • 这个思路进行的步数其实就是b二进制的位数，而他的位数其实就是b不断除2得到的，能被2除一次，位数就多1位
  • 因此O = 位数 = logb = logn

那么我们就可以给出下面的代码了

int pow(int a,int b){
    // 用ans来记录结果
    int ans = 1;
    while(b != 0){
        // 我们将a ^ b分为了若干个次方的积，而小次方的个数实际就是b二进制中1的个数
        // 如果b二进制个位目前为1，说明里面有一个a ^ x
        if(b & 1 == 1){
            // 把一个小次方乘到ans中，求出了一部分积
            ans *= a;
        }
        // 将a的次方翻倍，也就是a ^ [2 ^ (n-1)],这是我们每次小次方的更新
        // 更新结果就是a^1 a^2 a^4 a^8.....
        a *= a;
        // b右移1，删去一位二进制数，也就是更新个位数
        // 对于例子来说就是1101 110 11 1 0（省略的前导0）
        b = b >> 1;
    }
    
    return ans;
}

6.找出重复的数

注意题目要求：数组中，只有一个数出现奇数次，剩下都出现偶数次，找出出现奇数次的

这里与3中用的公式一样

• 任何数与0按位异或的结果都是他本身
• 任何数和自己按位异或的结果为0（每一位都相同，每一位结果都是0）

所以我们只需要设一个变量为0，将数组中所有数都与这个变量进行按位异或，那么最终这个变量的结果就是答案

我们可以进行一个模拟

• 数组为[a , b , b , c ,c]，这个数组里面数随机打乱，这里只是为了方便看所以写的是有序数组
• 设ans = 0
• 进行运算ans = ans ^ a ^ b ^ b ^ c ^ c = 0 ^ a ^ (b ^ b) ^ (c ^ c) = 0 ^ a ^ 0 ^ 0 = a

代码如下

#include<iostream>
using namespace std;
int main(){
    int a[9]={4,3,2,2,2,2,5,4,3};
    int ans=0;
    for(int i=0;i<9;i++){
        ans^=a[i];
    }
    cout<<ans;
    return 0;
}

7.用O(1)时间检测整数n是否是2的幂次

对于2的幂次n，他的二进制应该符合下面两个规律

• n > 0
• n的二进制里面只有一个1，因为2 ^ a + 2 ^ b一定不是2的幂次（证明方法网上搜）

因此，如果我们忽略前导0，那么n的二进制应该是100....0这样的，那么我们在十进制方面的n-1就应该是11...11（位数比n的少一位）。

假如n的二进制有x位，那么进行n & (n-1)，前x-1位都是0 & 1 = 0，第x位是1 & 0 = 0（&后面的0是n-1二进制的前导0），所以总体答案应该是n & (n-1) == 0。

通过反证法可知非2幂次数不满足这个条件

因此代码如下

#include<iostream>
using namespace std;
int main(){
    int n;
    cin>>n;
    if(!(n&(n-1))) cout<<"YES";
    if(n&(n-1)) cout<<"NO";
    return 0;
}

结语

位运算的用法多了去了，我真写不动了，我上面写的都是我查资料发现的简单一点的用法。

如果以后做题遇到新的我再补充，到时候估计会专门写个题解

写这篇，还有上一篇那个原码反码补码真的用了我好长时间。