算法基础1.5双指针算法

前言

双指针算法其实在前面已经用过很多次了，需要注意的是，这里的“双指针”并不是说用两个指针，而是使用“指针”这个抽象的思想，比如用一个变量也可以作为指针。

指针最常见的作用就是将一个需要嵌套循环的代码(时间复杂度为O(n^2))变成一个单循环的代码(时间复杂度是x*n，即O(n))。我们本来是两个变量i和j嵌套循环各n次，现在我们通过挖掘两者在题目中的关系，来减少一些无用的i``j组合

该节里面讲了道题作为引导

正文

题目与代码

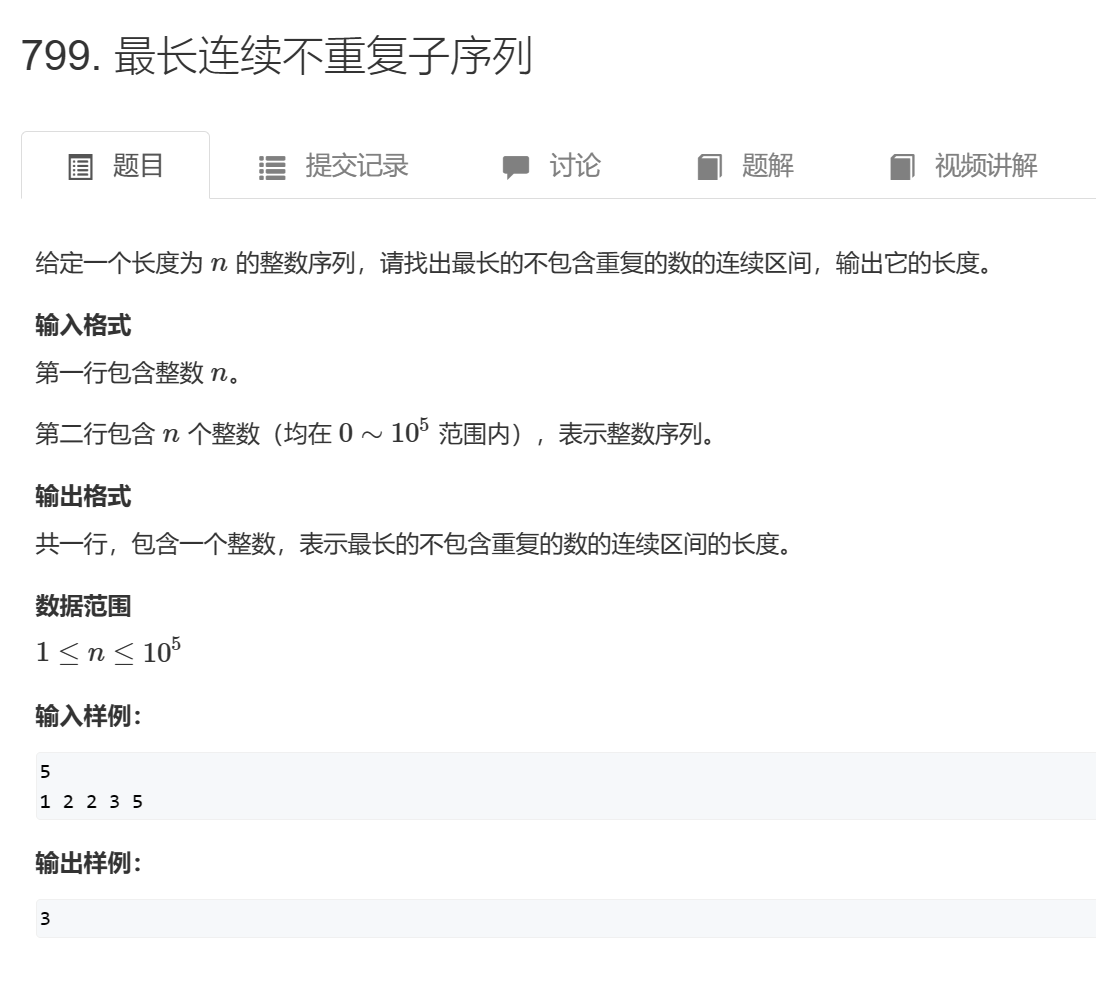
代码如下

#include <iostream>

using namespace std;

const int N = 100010;

int n;
int q[N], s[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
	// 记录区间长度
    int res = 0;
    for (int i = 0, j = 0; i < n; i ++ )
    {
        // i移动，记录区间中新增的数
        s[q[i]] ++ ;
        // 如果某一个数出现的次数超过1次（其实只能是2次），那么j开始移动
        // s[q[j ++ ]] --这个语句先让s[q[j]]--，然后再j+1
        while (j < i && s[q[i]] > 1) s[q[j ++ ]] -- ;
        // 看看更新后区间有没有变长
        res = max(res, i - j + 1);
    }

    cout << res << endl;

    return 0;
}

分析

这道题我们使用双指针，i指向这个最长序列的最右端，他是一个遍历的指针，j指向这个最长序列的最左端，他是一个依赖于i而变化的指针。如此，j就不需要进行嵌套循环了，他只需要在特定条件下变化即可。

先明确大体思路：一开始两个指针都指向了数组第0位，然后i开始向右移动，j不动。直至i``j两个指针夹着的这个区间中出现了重复的数，那么i不动，j开始移动，一直移动到区间内再次没有重复的数（实际上i结束移动说明现在i指向的那个数就是这个区间中某一个数的第二份，所以j停止移动的节点就是移动到这个数第一次出现的位置的后面一位）。

大体思路定下来了，最后只要实现一下记录区间中有哪些数这一功能即可，这个单独在创建一个数组即可，他的x位上的数值就代表当前区间中x这个数出现的次数。每次i移动都会让某一位置+1，而j每次移动都会让某一个位置-1。

注意：res的更新要让当前值与原先值作比较取最大值，因为更新后有可能长度变短。

结语

大体思路就是：先通过暴力的思路写出来代码，然后思考其中两个变量之间的线性关系，通过这种关系将时间复杂度从O(n^2)降到O(n)