 代数系统的定义
代数系统的定义代数的构成和分类的方法

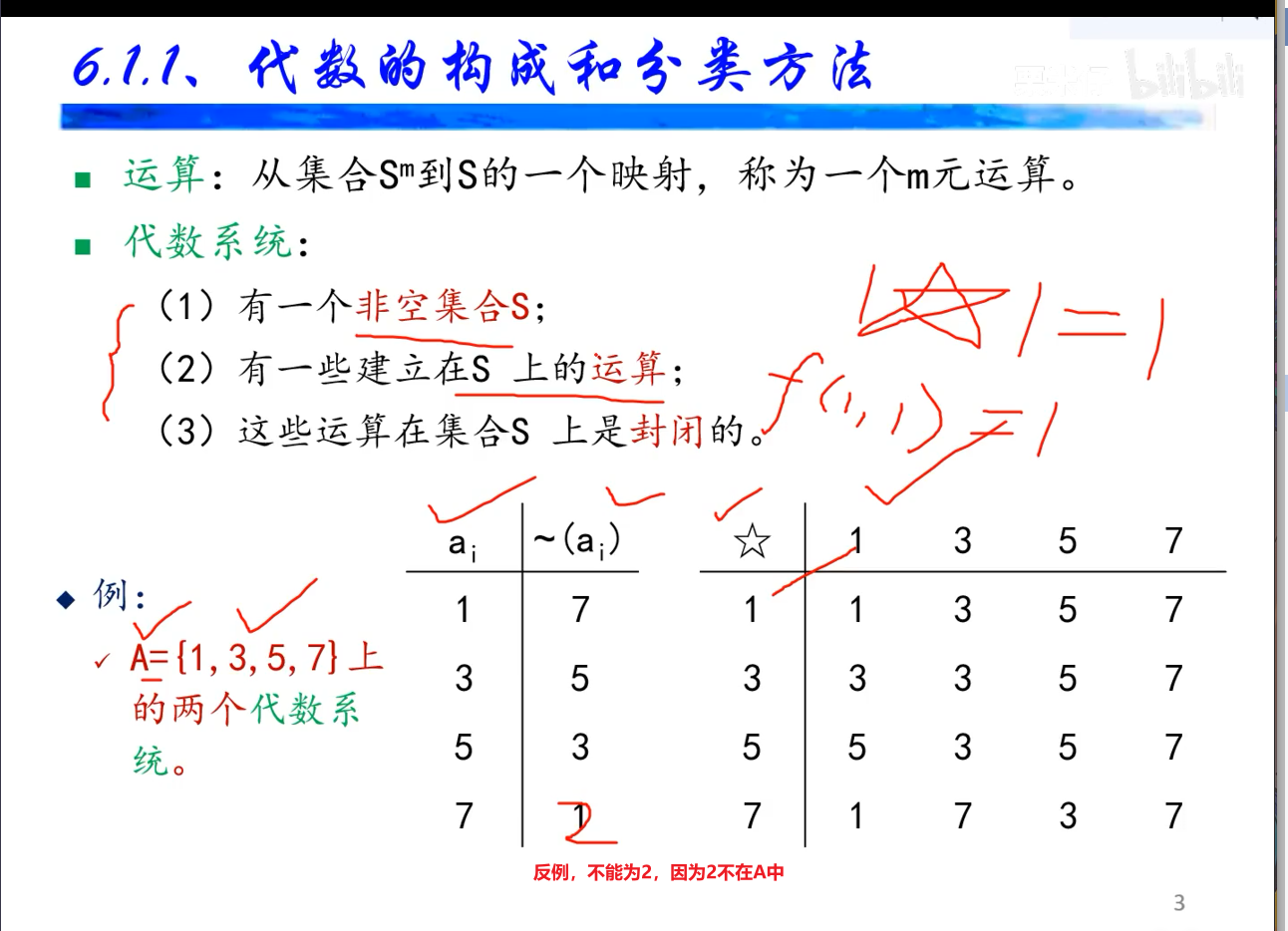
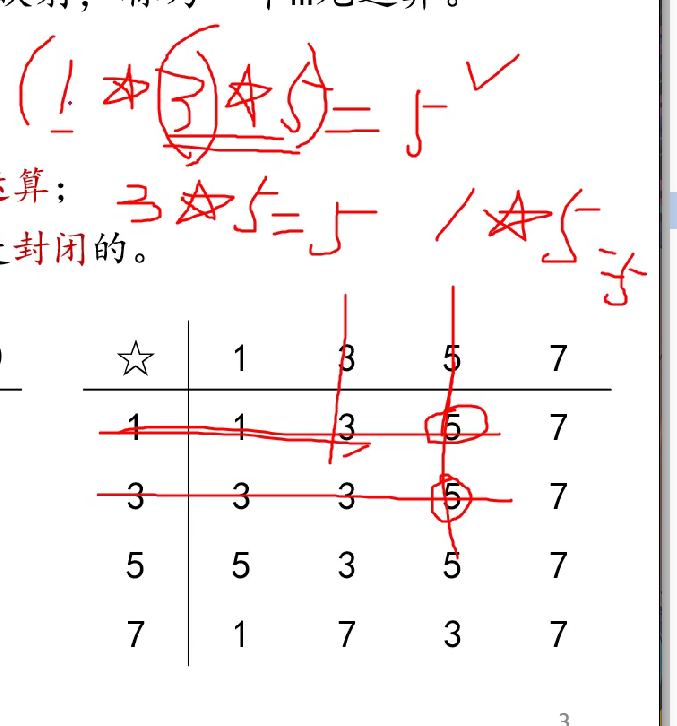
当判断某个代数系统是否满足结合律,交换律,分配律,德摩根律等时要吧该系统中每个元素所有组合都考虑到,一旦有一个元素或一个组合不符合某定律,则该系统不适合该定律

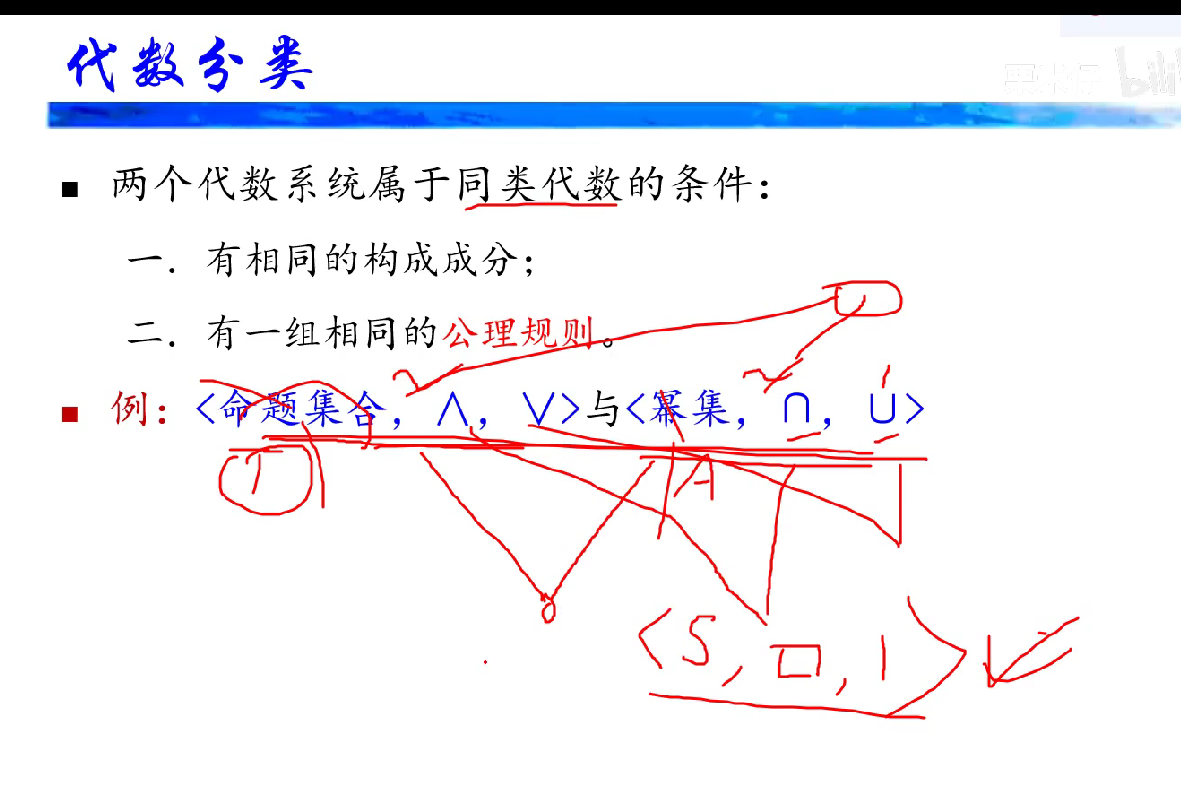

 么元、零元、逆元
么元、零元、逆元 么元、零元
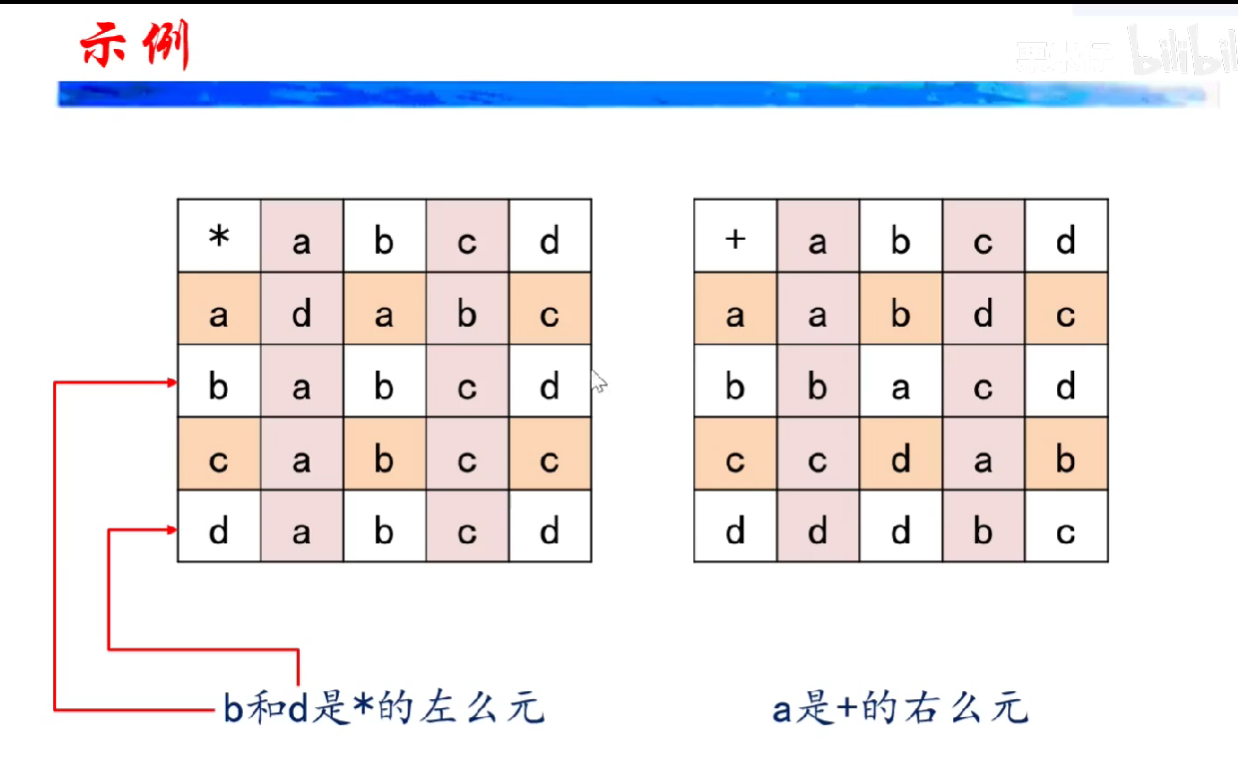
么元:设有一个运算符号#是在集合s上的二元运算,S={a,b,c}
则(a#b=b ^ a#c=c) ^ (b#a = b ^ c#a =c) = True;
则称a对于#是么元;
零元:设有一个运算符号¥是在集合s上的二元运算,S={a,b,c}
则(a¥b=a ^ a¥c=a) ^ (b¥a = a ^ c¥a =a) = True;
则称a对于¥是零元;

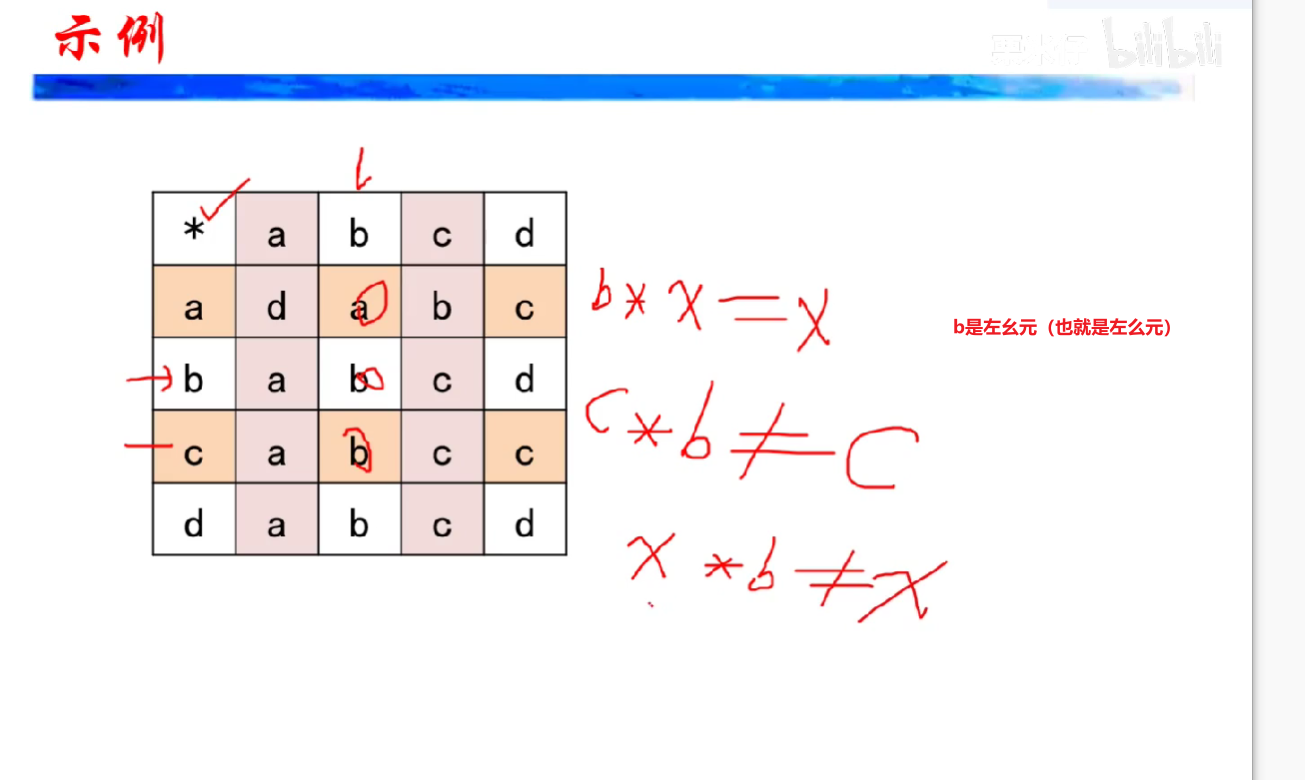
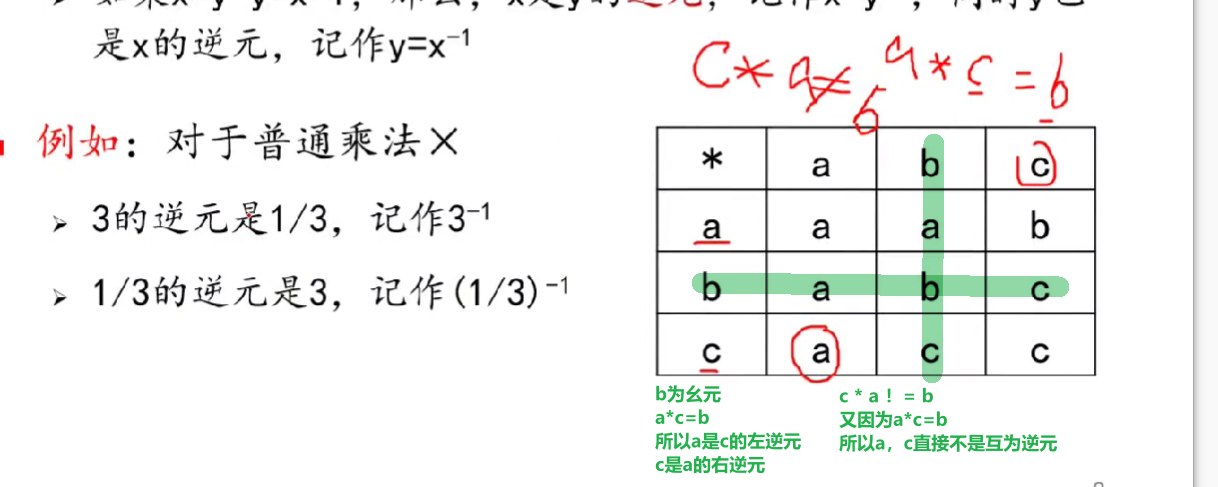
逆元


 子代数
子代数



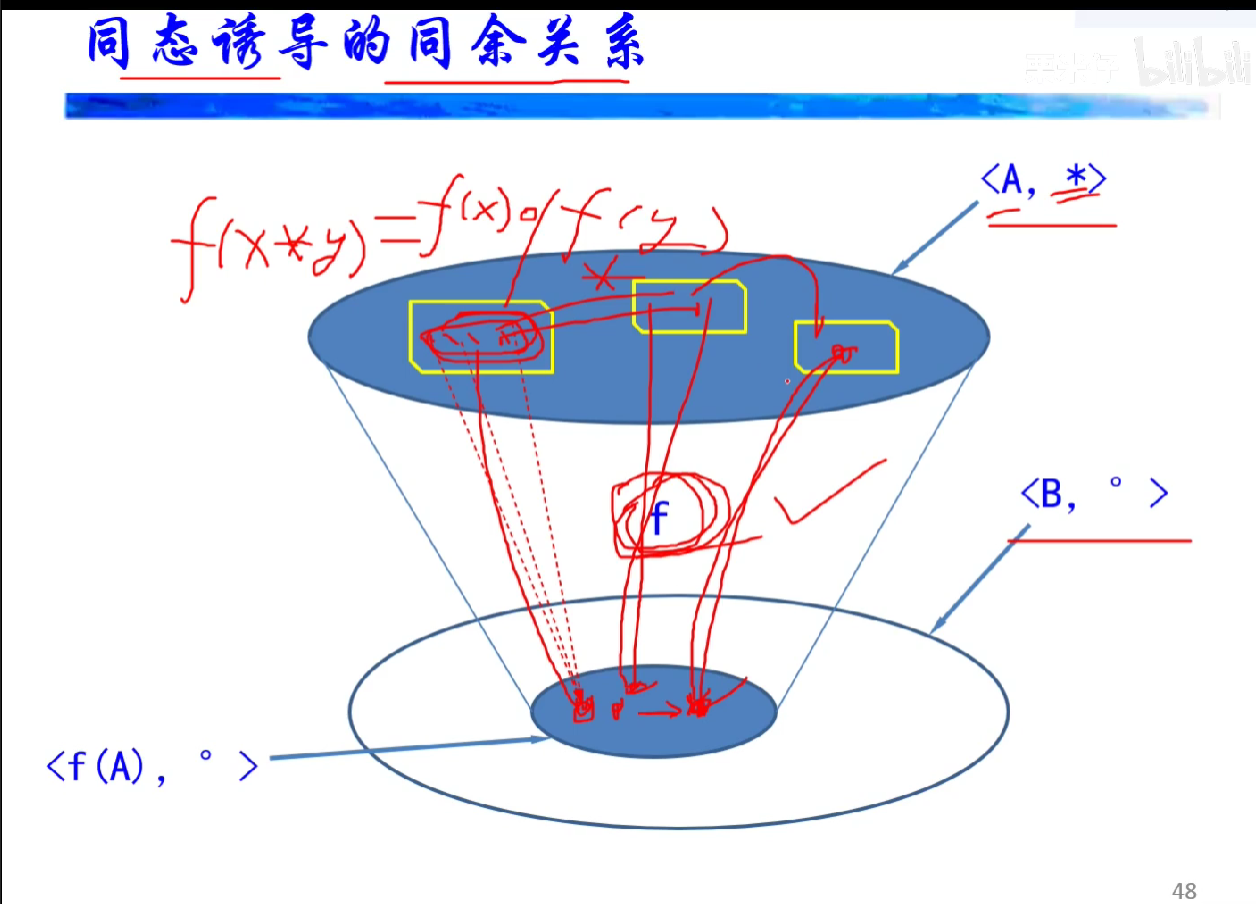
 同态
同态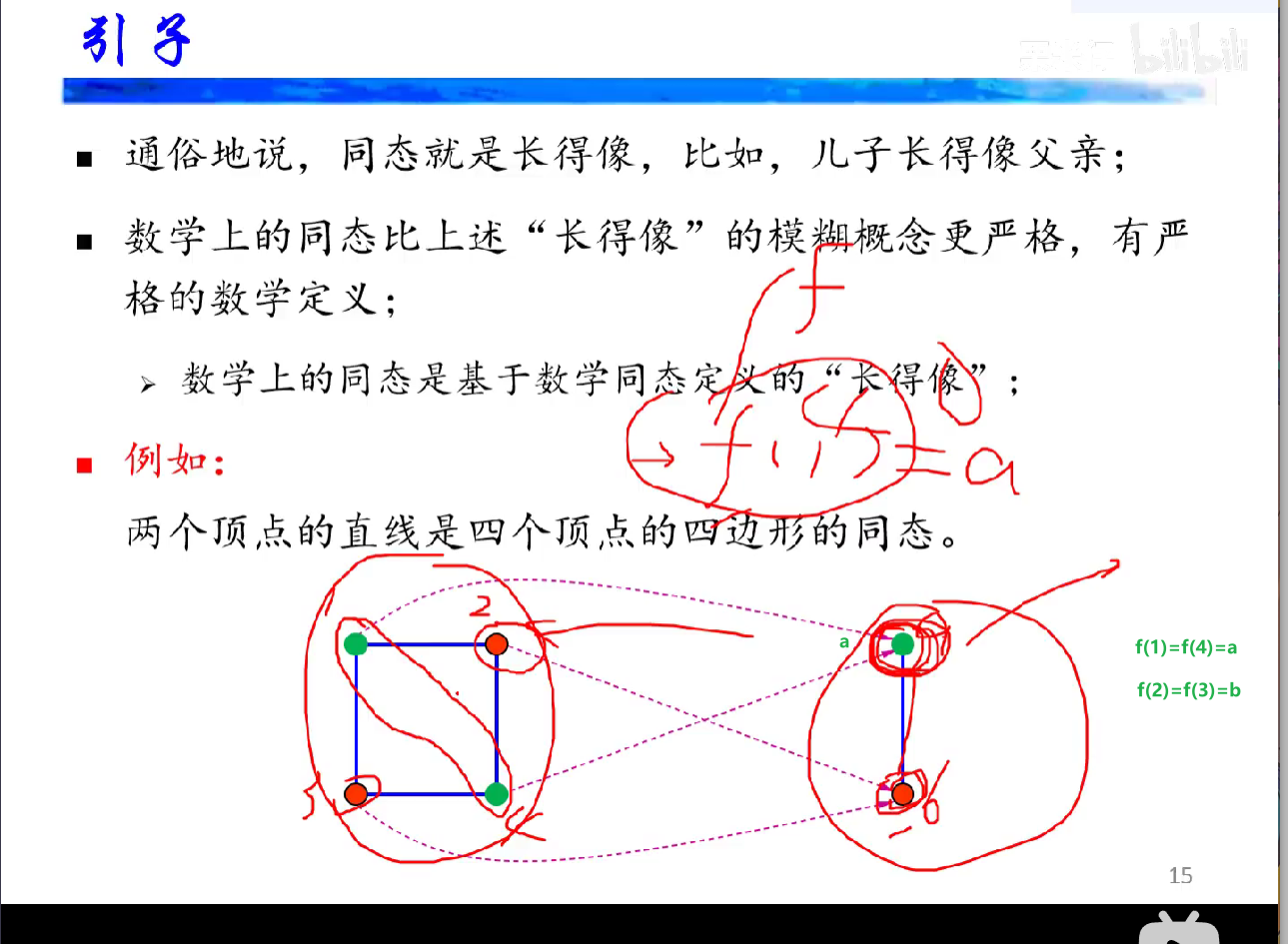
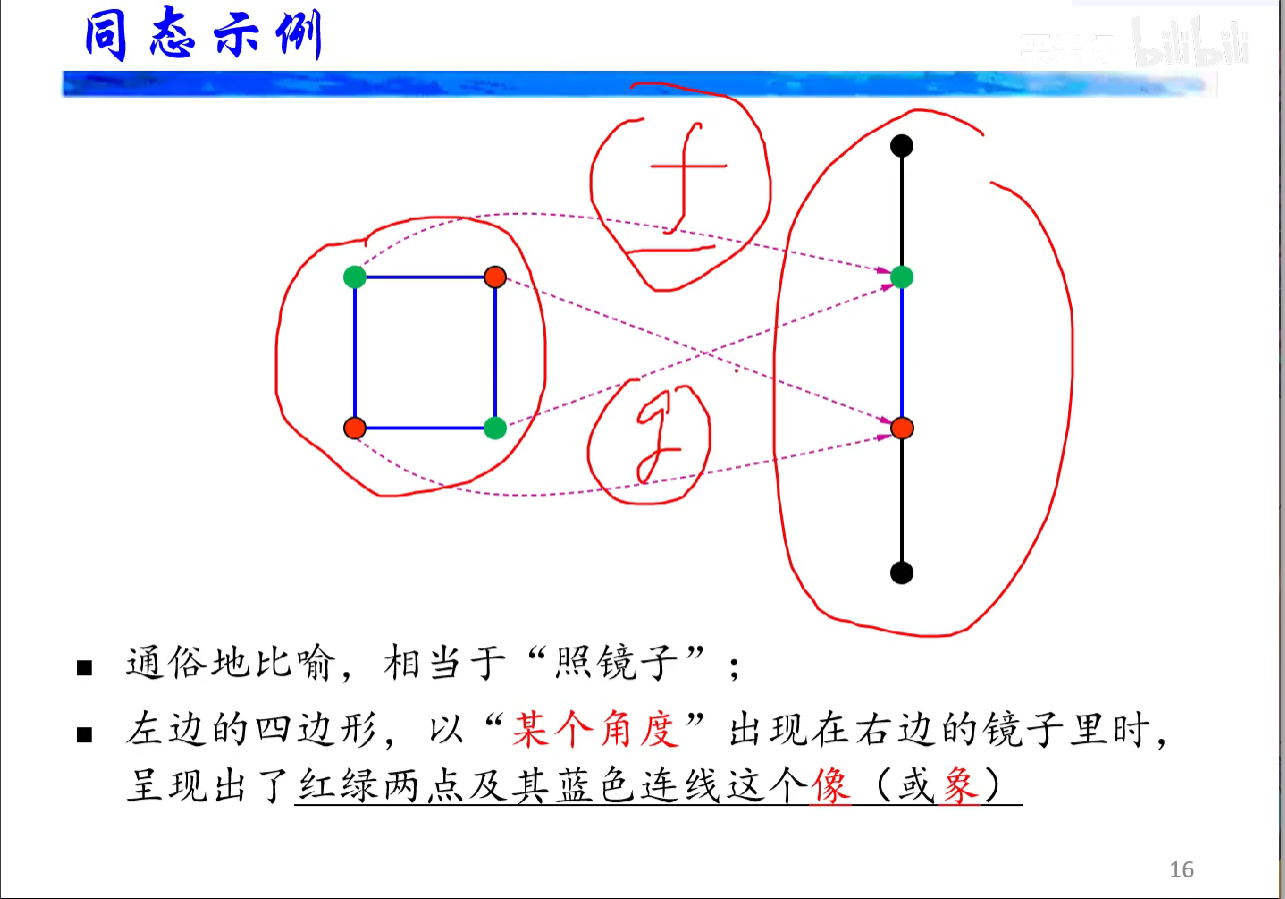

 同态图解、同构
同态图解、同构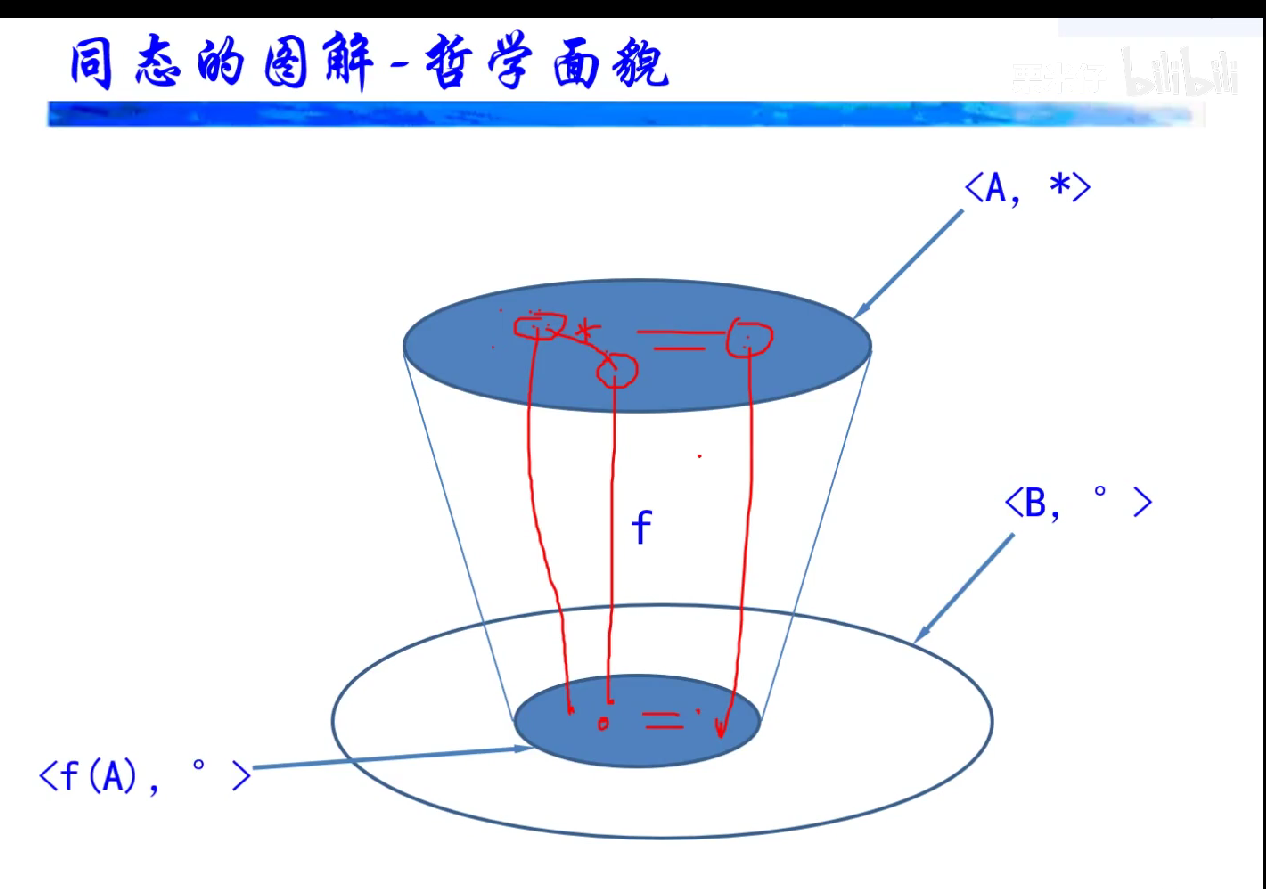
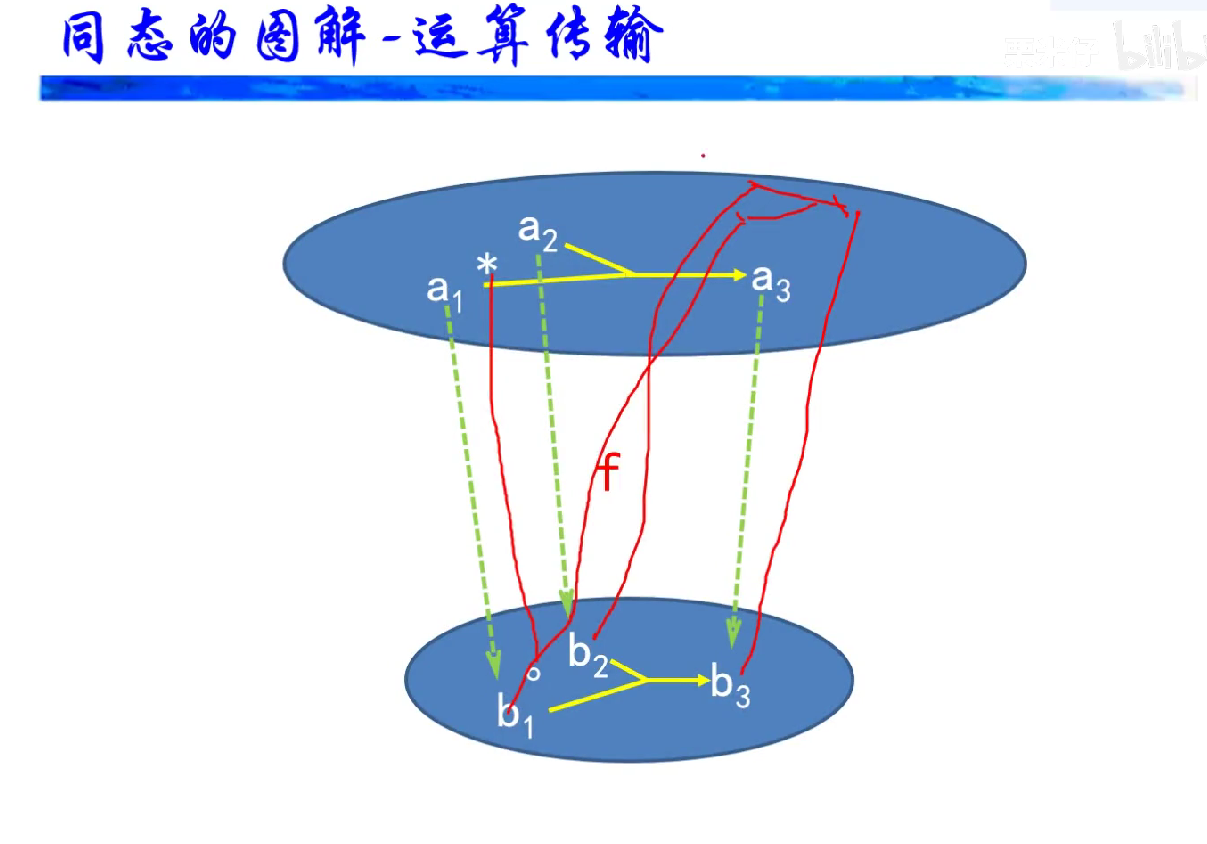
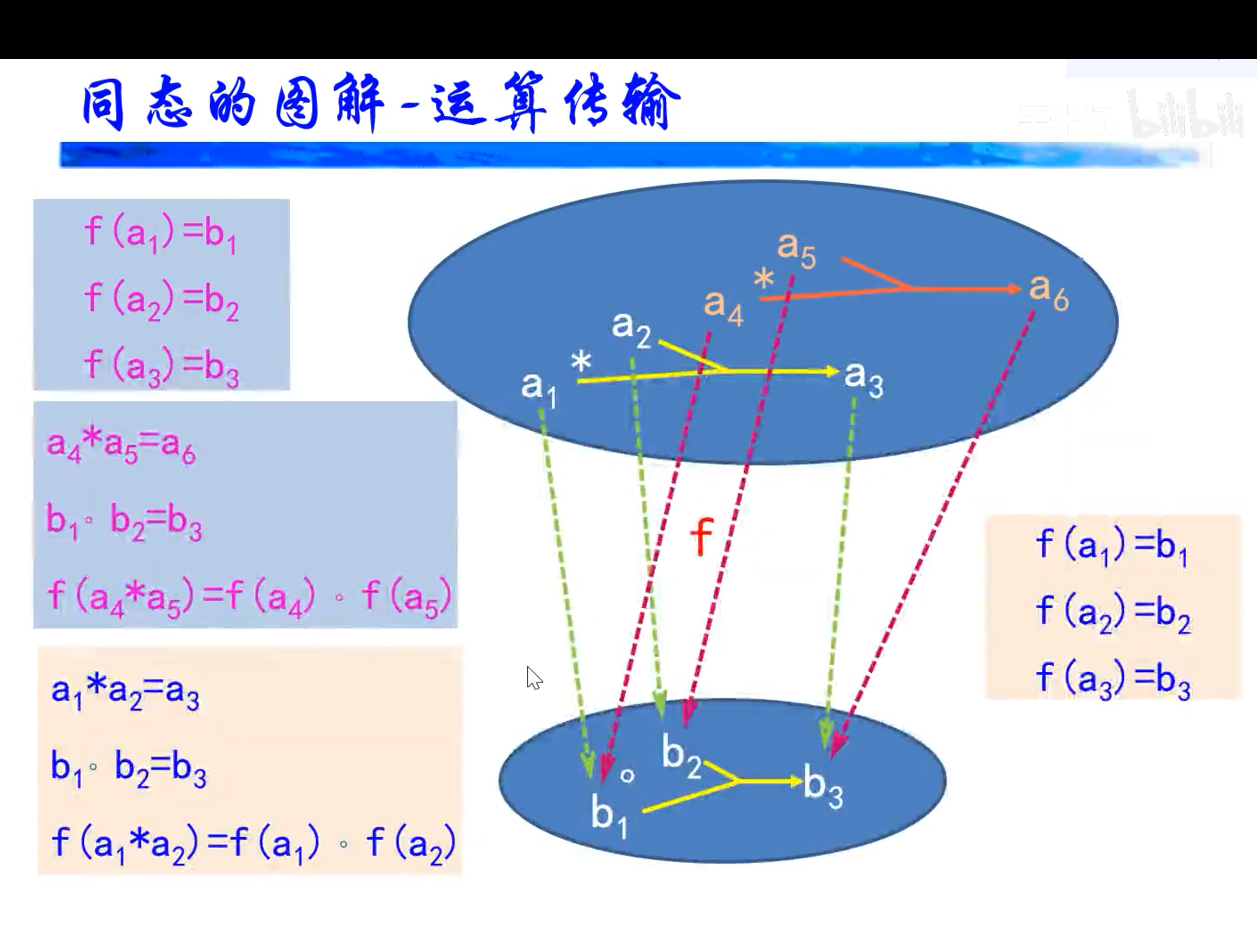

单同态就是漫同态,满同态不一定是单同态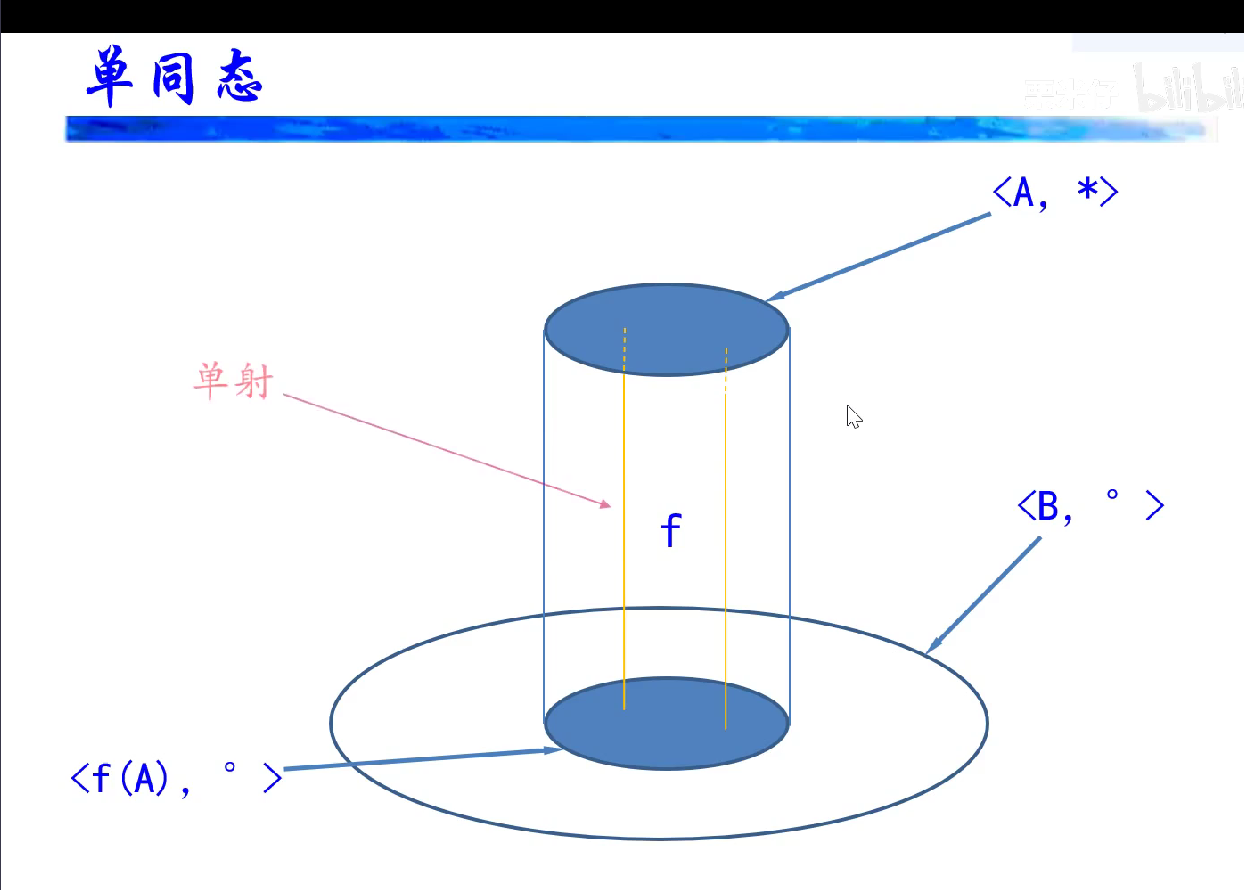
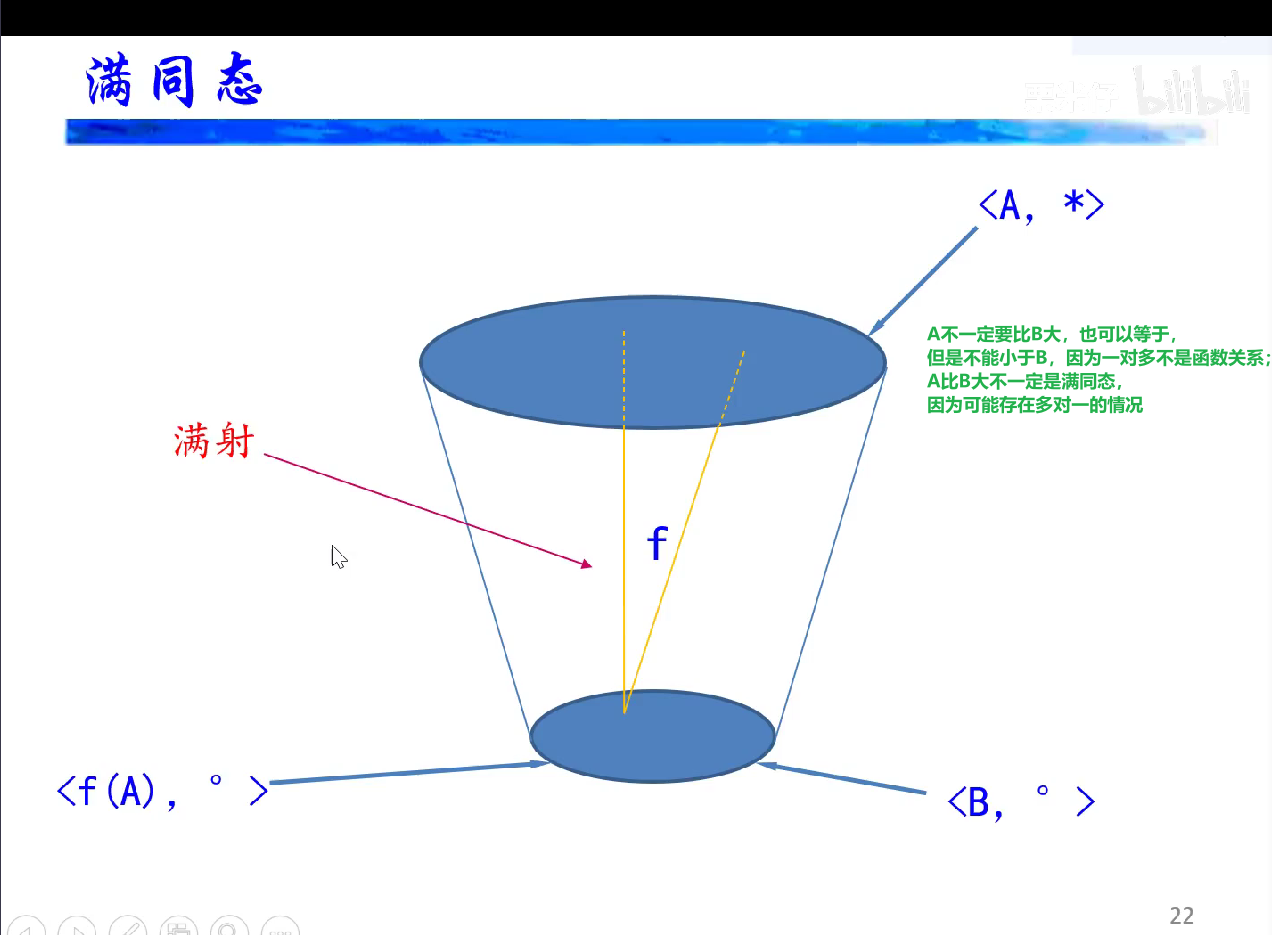
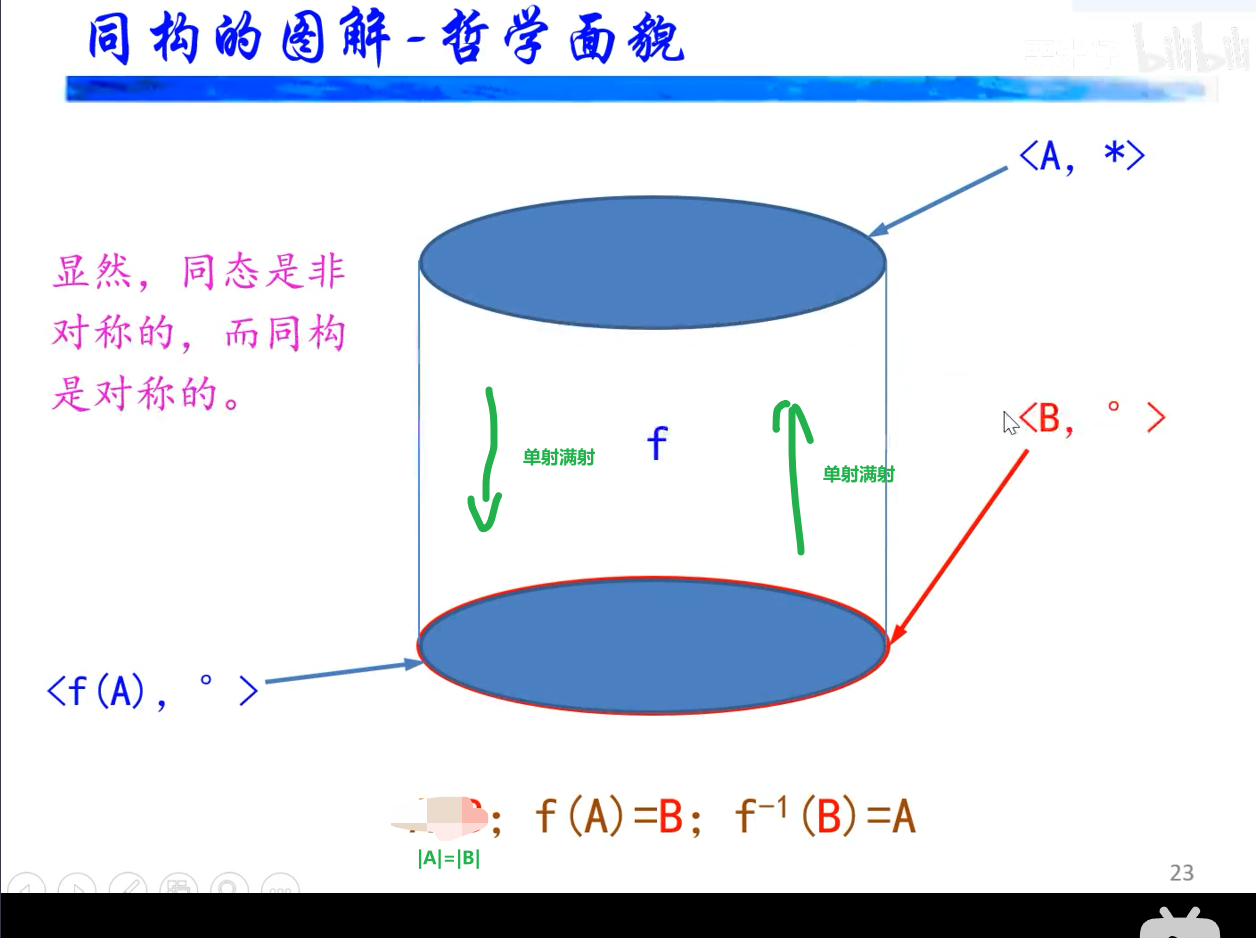



 自同态、同态像与陪域、前域的关系
自同态、同态像与陪域、前域的关系 自同态

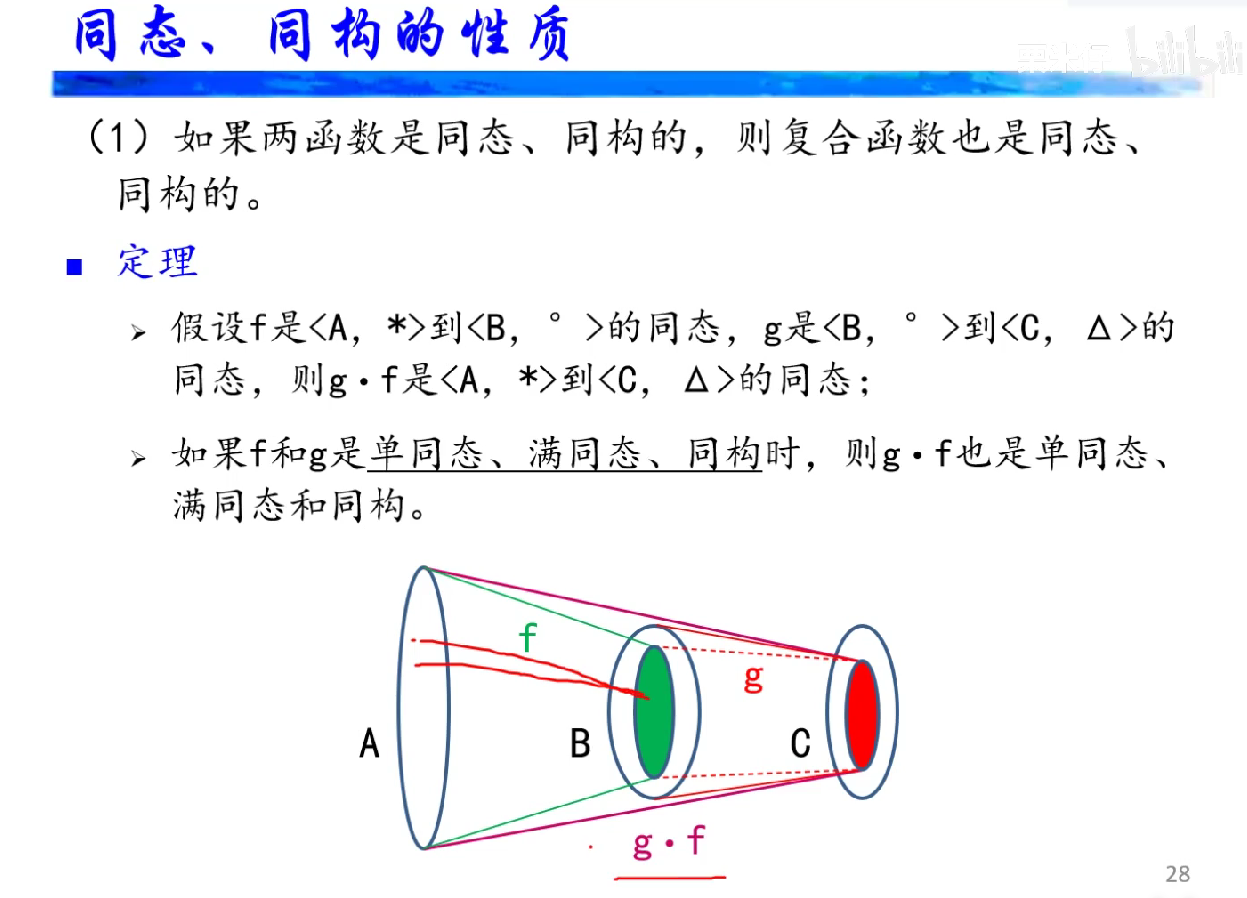
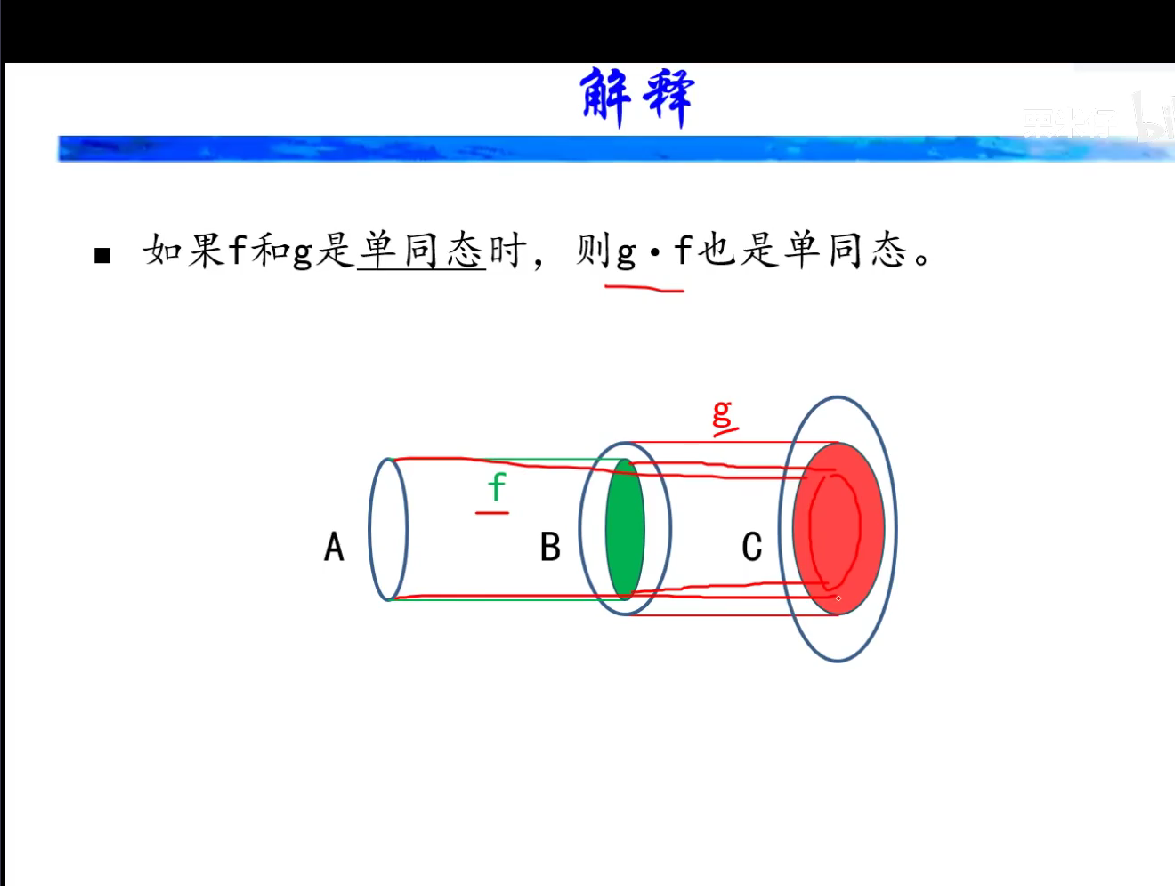



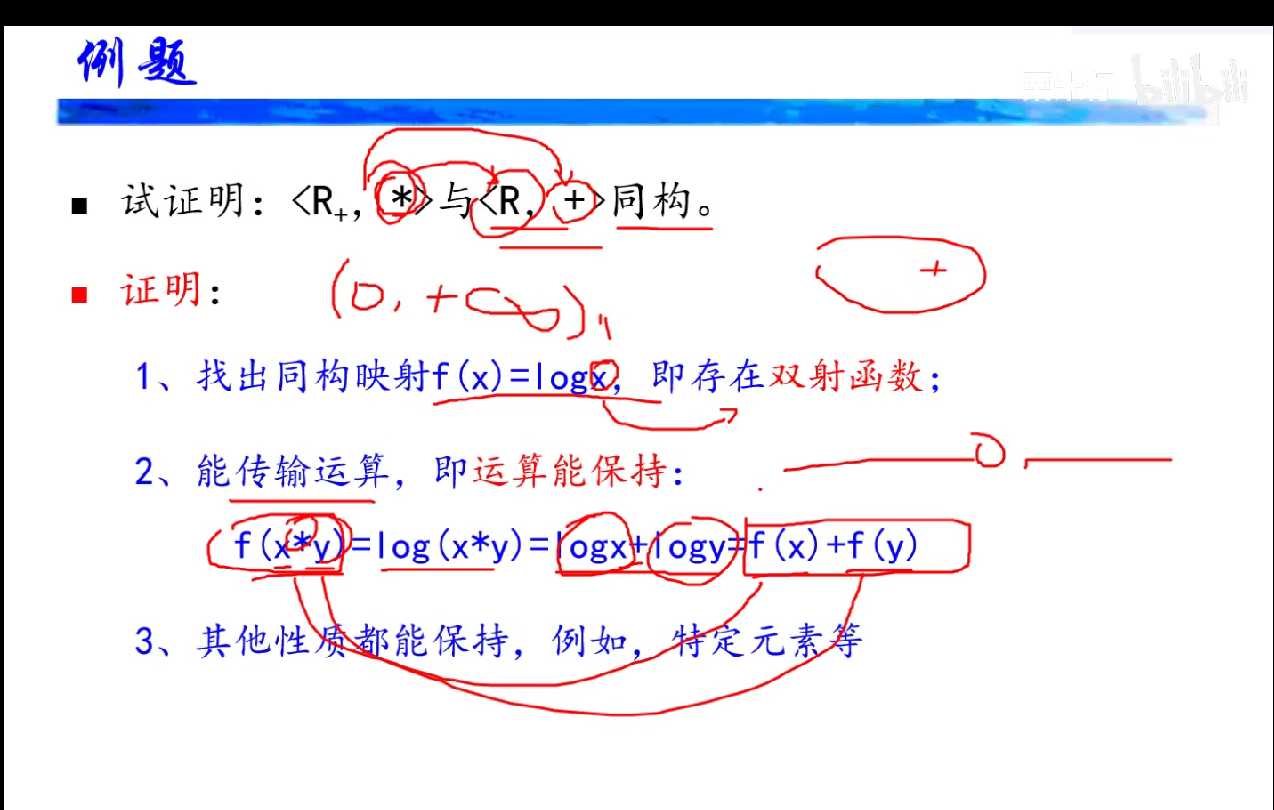
同态像与陪域、前域的关系

 同余关系
同余关系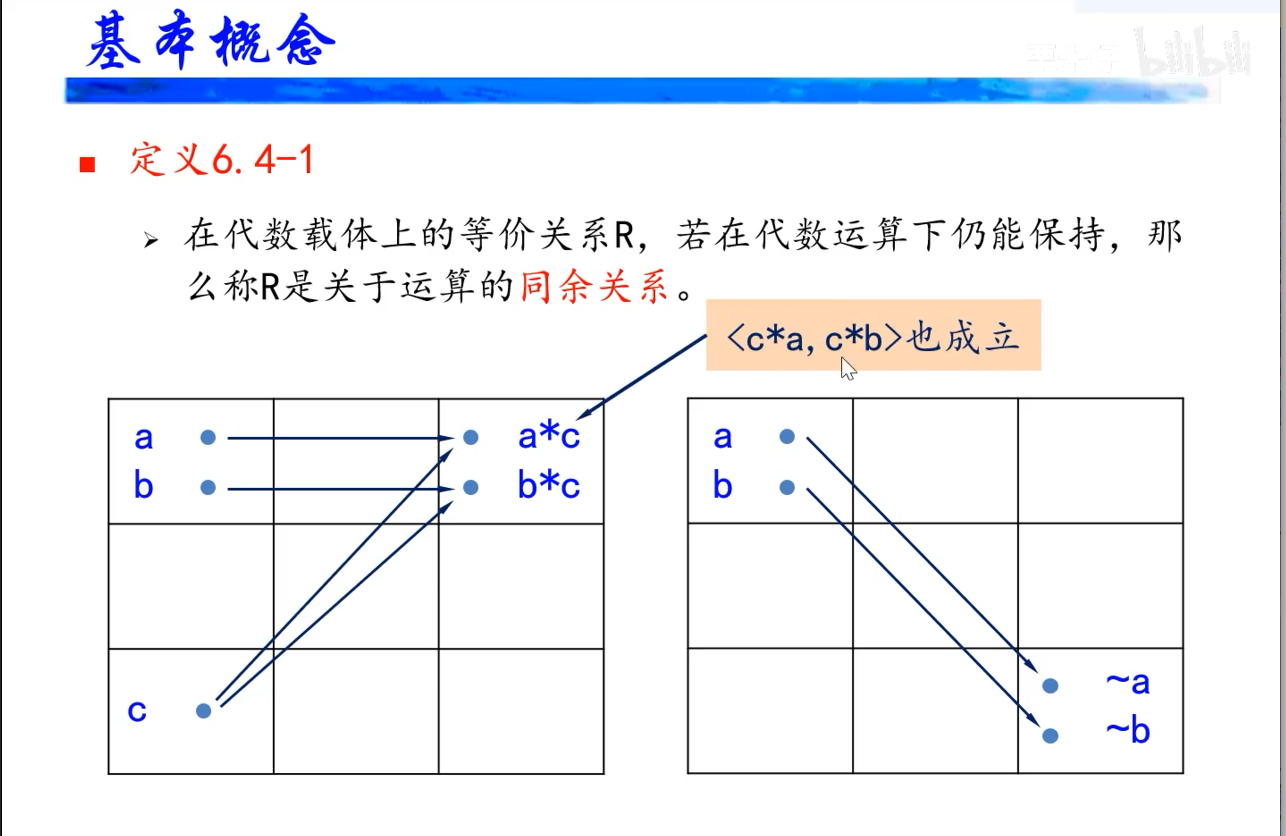





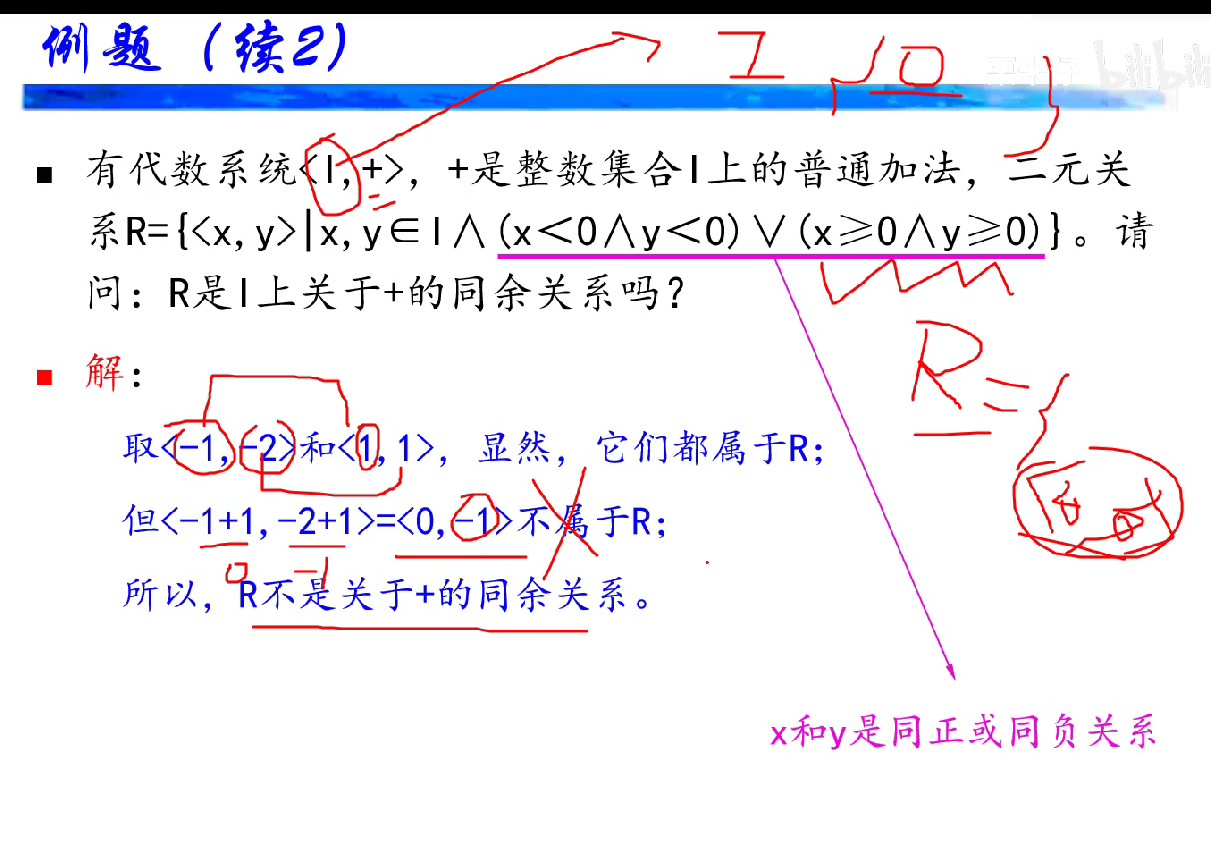

 商代数、积代数
商代数、积代数
商代数



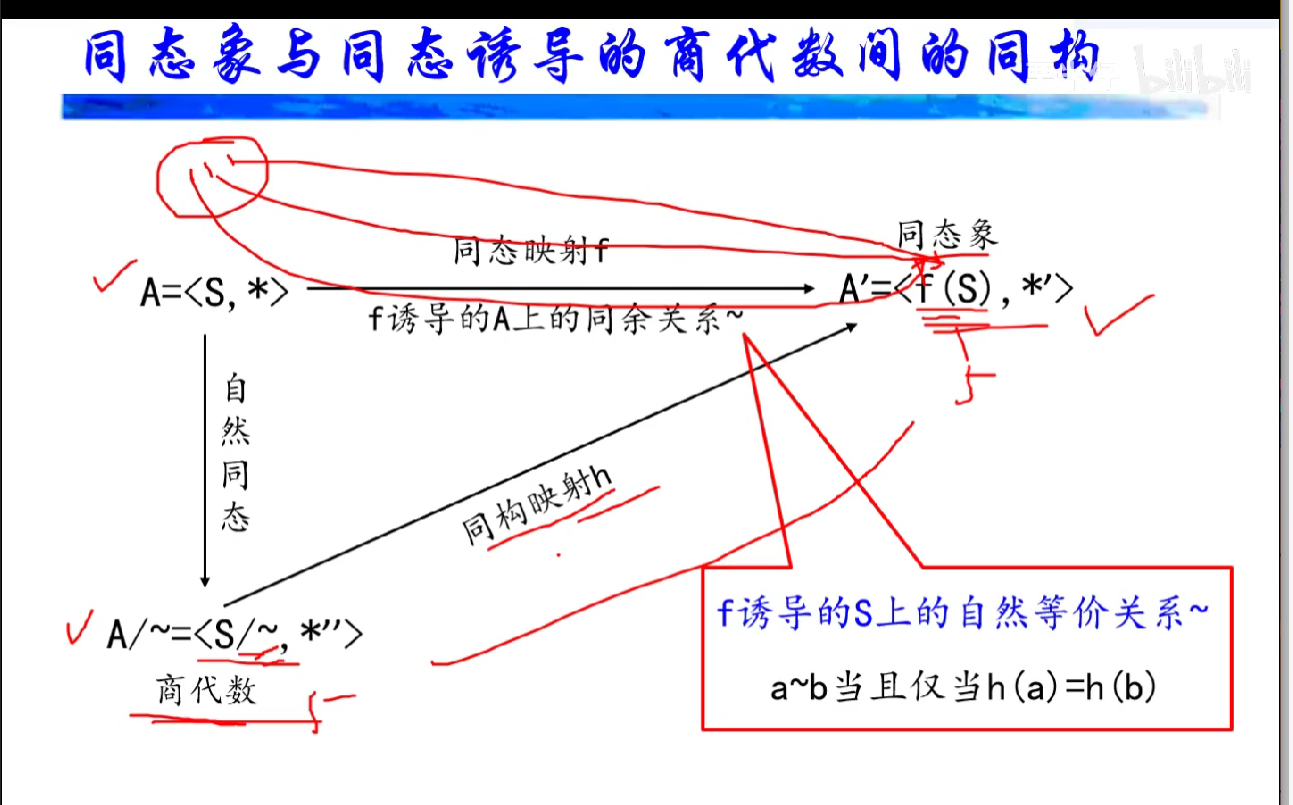
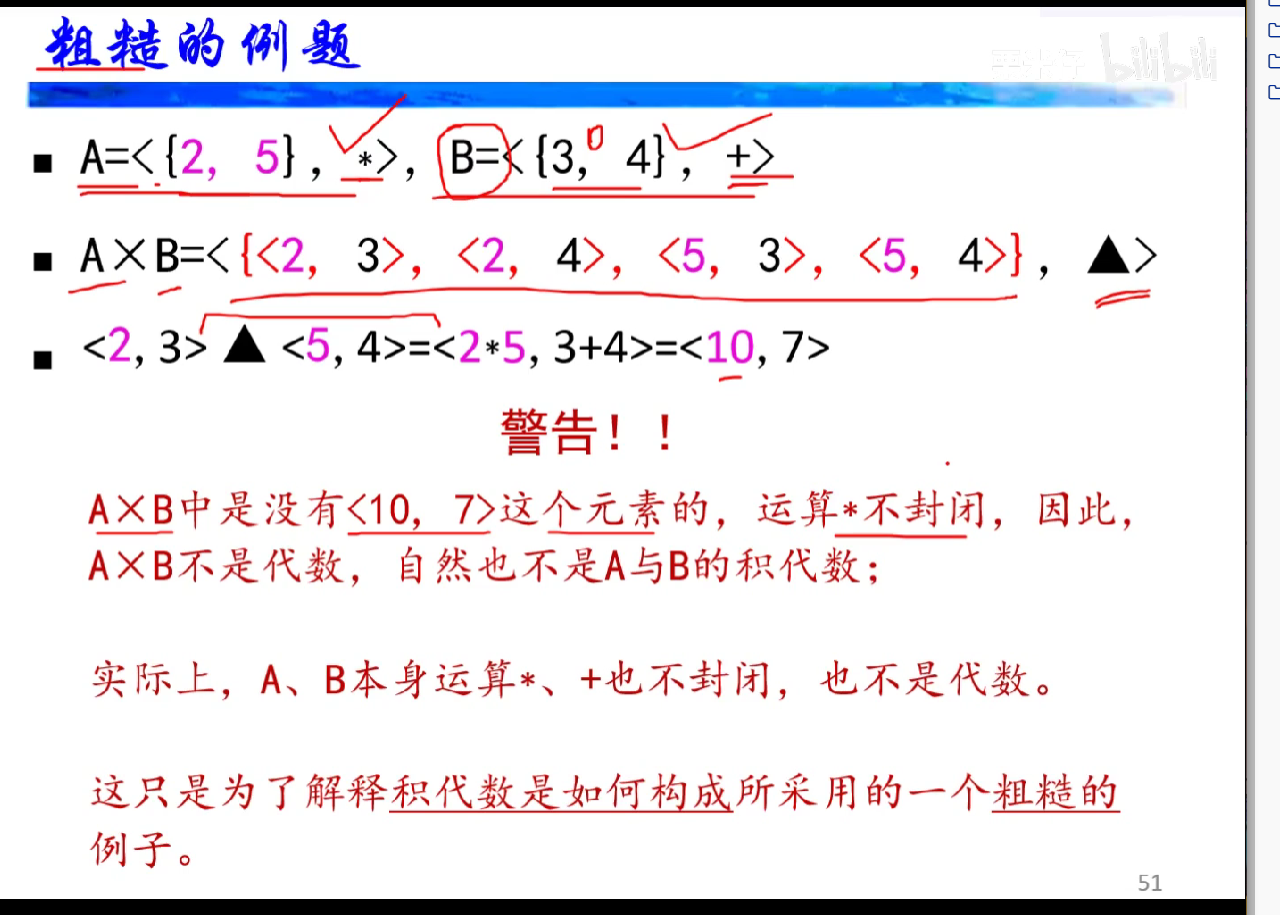
积代数







 浙公网安备 33010602011771号
浙公网安备 33010602011771号