2025.7.24 模拟赛 T3

题意

点击查看代码

#include<bits/stdc++.h>

#define LL long long
#define ull unsigned long long
#define F(i, j, k) for (int i = (j); i <= (k); i++)
#define DF(i, j, k) for (int i = (j); i >= (k); i--)
using namespace std;
template < typename T > inline void read(T & n) {
    T w = 1;
    n = 0;
    char ch = getchar();
    while (!isdigit(ch) && ch != EOF) {
        if (ch == '-') w = -1;
        ch = getchar();
    }
    while (isdigit(ch) && ch != EOF) {
        n = (n << 1) + (n << 3) + (ch ^ 48);
        ch
        n *= w;
    }
}
template < typename T > inline void write(T x) {
    ull y = 0;
    T l = 0;
    if (x < 0) {
        x = -x;
        putchar('-');
    }
    if (!x) {
        putchar(48);
        return;
    }
    while (x) {
        y = y * 10 + x % 10;
        x /= 10;
        l++;
    }
    while (l) {
        putchar(y % 10 + 48);
        y /= 10;
        l--;
    }
}
template < typename T > inline void writeln(T x) {
    write(x);
    puts("");
}
template < typename T > inline void writes(T x) {
    write(x);
    putchar(' ');
}
template < typename T > inline void checkmax(T & a, T b) {
    a = a > b ? a : b;
}
template < typename T > inline void checkmin(T & a, T b) {
    a = a < b ? a : b;
}
const int M = 1e6 + 10;
int tot;
struct node {
    int lc, rc, l, r, mid, sum;
}
t[M << 2];
int random(int l, int r) {
    return rand() % (r - l + 1) + l;
}
int build(int l, int r) {
    int x = ++tot;
    t[x].l = l;
    t[x].r = r;
    if (l == r) return x;
    int mid = random(l, r - 1);
    t[x].mid = mid;
    t[x].lc = build(l, mid);
    t[x].rc = build(mid + 1, r);
    return x;
}
void update(int x, int p) {
    t[x].sum++;
    if (t[x].l == t[x].r) return;
    if (p <= t[x].mid) update(t[x].lc, p);
    else update(t[x].rc, p);
}
int query(int x, int l, int r) {
    if (l <= t[x].l && t[x].r <= r) return t[x].sum;
    int ret = 0;
    if (t[x].mid >= l) ret += query(t[x].lc, l, r);
    if (t[x].mid + 1 <= r) ret += query(t[x].rc, l, r);
    return ret;
}
int n, m;
int main() {
    read(n);
    read(m);
    srand(time(0));
    int rt = build(1, n);
    F(i, 1, m) {
        int op, x, l, r;
        read(op);
        if (op == 1) read(x), update(rt, x);
        else read(l), read(r), writeln(query(rt, l, r));
    }
    return 0;
}

输入格式

数据范围

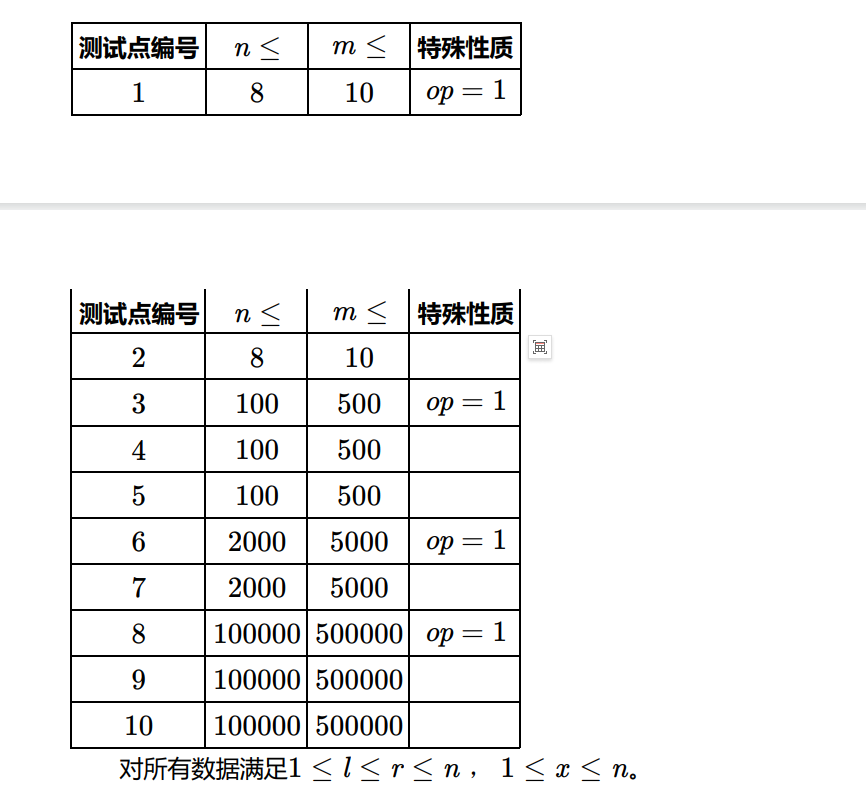
做法

一些声明

• \(opt=1\) 实际上等价于 \(opt=2\) 中 \(l=r\) 的情况。

• 每次选择 \(mid\) 的过程，实际上就是用刀切在 \(mid+0.5\) 的位置把区间切成两半。

  注意这里切点是个小数，所以我们下面 \(mid\in(l,r)\) 指的就是切在 \(l\sim r\) 这些数的缝隙中。

• 下面可能用“递归次数”表示题目中的贡献数。

具体做法

记 \(f_i\) 为一共有 \(i\) 刀可切，切到边上 \(1\) 刀以前（含边上这刀）的期望步数。这个容易用前缀和优化做到 \(O(n)\)。

尝试按照 \(l,r\) 进行分讨计算：

• \(l=1,r=n\)

  答案为 \(1\)

• \(l=1,r<n\) 或者 \(l>1,r=n\)

  两种情况对称且本质相同，仅考虑 \(l=1,r<n\)。

  根据期望的线性性，我们把所有同种切法放在一起考虑。同时，下面先不阐述 \(O(1)\) 种算重的情况。

  • Case 1.1：考虑切线区间 \([1.5,r+0.5]\)，每次砍一刀左右两边都会产生 \(1\) 的贡献，然后只会往右继续递归下去计算。当切在 \(r-0.5\) 的位置的时候停止往下递归。贡献和为 \(2f_r\)。
  • Case 1.2：考虑切线区间 \([r+0.5,n-0.5]\)，每次砍一刀会往左边递归，右边不会产生贡献。总贡献是 \(f_{n-r}\)。

  考虑一开始整个区间有贡献 \(1\) 得加上；\(2f_r\) 实际上把切线 \(r+0.5\) 多算了 \(2\) 次，要减去。

  故而答案为 \(2(f_r-1)+f_{n-r}+1\)。

• \(l>1,r<n\)

  类似的方法（同样先不考虑 \(O(1)\) 个算重）：

  • Case 2.1 and 2.2：考虑切线区间 \([1.5,l-0.5]\) 和 \([r+0.5,n-0.5]\)，使用和上面一样的方法，贡献为 \(f_{l-1}\) 和 \(f_{n-r}\)
  • Case 2.3：考虑切线区间 \([l-0.5,r+0.5]\)，这个区间中的第一刀切下之后，每次会往两边做类似 Case1.2 的东西吗，每边的方案数都是 \(2f_{r-l+2}\).

  考虑整个区间有贡献 \(1\) 得加上；两个 \(2f_{r-l+2}\) 分别把切线 \(l-0.5,r+0.5\) 多算了各两次。然后考虑计算 Case2.3 时切在区间内的第一刀贡献会算重 \(2\)，减去即可。

  故而答案为 \((2(f_{r-l+1})-1)\times 2 + f_{l-1}+f_{n-r}\)

代码实现

点击查看代码

#include <bits/stdc++.h>
#define FL(i, a, b) for (int i = (a); i <= (b); ++i)
#define FR(i, a, b) for (int i = (a); i >= (b); --i)
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
const int MOD = 998244353;
int n, m, f[N], inv[N];
void AddTo(int &x, int y) {
    x = (x + y >= MOD? x + y - MOD : x + y);
}
int Sub(int x, int y) {
	return x < y? x + MOD - y : x - y;
}
int Mul(int x, int y) {
    return (ll)x * y % MOD;
}
int main() {
    freopen("random.in", "r", stdin);
    freopen("random.out", "w", stdout);
    scanf("%d %d", &n, &m);
    FL(i, 1, n) {
        inv[i] = (i == 1? 1 : Mul(inv[MOD % i], MOD - MOD / i));
    }
	int sum = 0;
    FL(i, 1, n) {
        f[i] = (Mul(sum, inv[i]) + 1) % MOD;
        AddTo(sum, f[i]);
    }
    FL(i, 1, m) {
		int opt, l, r, x, ans, len;
        scanf("%d", &opt);
        if (opt == 1) {
            scanf("%d", &l), r = l;
		} else {
			scanf("%d %d", &l, &r);
		}

		ans = 1, len = r - l + 1;
		if (l == 1 && r == n) {
		} else if (l == 1) {
			AddTo(ans, f[n - r]);
			AddTo(ans, Mul(2, Sub(f[len], 1)));
		} else if (r == n) {
			AddTo(ans, f[l - 1]);
			AddTo(ans, Mul(2, Sub(f[len], 1)));
		} else {
			AddTo(ans, f[l - 1]);
			AddTo(ans, Sub(Mul(2, Sub(f[len + 1], 1)), 1));
			AddTo(ans, f[n - r]);
			AddTo(ans, Sub(Mul(2, Sub(f[len + 1], 1)), 1));
		}
        printf("%d\n", ans);
    }
    return 0;
}