[ABC284G] Only Once

题目大意

给你一个 $N$，让你求所有长度为 $N$ 的所有数字都在 $1 \to n$ 的范围内的 $A$ 数组他们的贡献之和。

我们设 $A_i$ 的贡献为 $S_i$。那么这时我们还有一个 $B$ 数组，对于每个 $B_{i,j}$，有 $1 \leq i \leq n$ 且 $1 \leq j \leq 10^{100}$，且 $B_i = (B_{i,1},B_{i,2}, B_{i,3}, ... ,B_{i,10^{100}})$。

$B$ 数组构造方式：

• $B_{i,1}=i$。
• $B_{i,j+1}=A_{B_{i,j}}(1 \leq j < 10^{100})$。

然后呢，对于每个 $S_i$，他等于 $B_i$ 中恰好只出现一次的数字个数。

所以当前的 $A$ 数组的答案就是 $S_i$ 之和，而最终答案要累加所有可行的 $A$。输出时对答案取模 $M$。

思路

多半题目第一步常见的是发现性质加模型转换。那我们思考这道题目中有什么性质呢？

首先我们发现答案的每一行有对称性，所以我们只要算出一行再乘以 $N$ 即可。

对于每一行，又该怎么算呢？这时候能发现如果我们把长度抽象成 $N$ 个点， $A$ 数组抽象成 $N$ 条边（$i$ 连向 $A_i$），$B_{i,1}=i$ 其实就是第 $i$ 行起点为 $i$，那么有良好的性质——因为一个点只有向着 $A_i$ 连边，所以只连出去了一条边，而这也就保证了我们从某个点开始走的话路上没有分叉，只能一条走到底，这也就意味着，如果走上了一个环，就再也走不出去了，那就说明路径上 至多只有一个环。

同样，你也会很快发现因为每个点都有连出去的边，所以永远都走不完，利用鸽巢原理可以证明，而当走到第 $N+1$ 个点时，必定有重复，而有重复就必定有环——至少有一个环。

把两个结论结合一下，那就是： 有且仅有一个环 。

如果还不够清晰，可以借助下图理解：

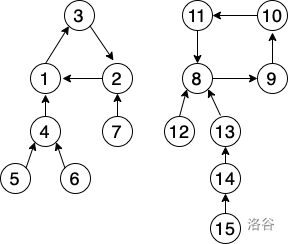
好了，接下来的就很简单了。我们设对于 $b_i$，从 $B_{i,l+1}$ 开始出现重复，其与 $B_{i,p}$ 重复了，其中 $p<l$，那么这时我们恰好出现一次的节点数是 $p-1$。原因非常简单，那就是因为从 $p$ 那个位置开始重复，意味着 $B_i$ 的 $1 \sim p-1$ 的位置不可能再遍历到了，而后面会一直循环遍历。

接下来就直接给出式子（我们枚举 $l$）：$$ A_{n-1}^{l-1}N^{N-l}\sum_{p=1}^l(p-1)=A_{n-1}^{l-1}*N^{N-l}*{l(l-1) \over 2} $$

其中上面的 $A_{n-1}^{l-1}$ 表示 $n-1$ 个点中选 $l-1$ 个（因为起点也算在 $l$ 个点内，且另外 $l-1$ 个点不得与起点重复）。而 $N^{N-l}$ 是因为第 $l+1$ 个位置与第 $p$ 个位置重复了，所以总共出现了 $l$ 种不同的数字，而另外 $n-l$ 中数字的 $A$ 数组值可以使 $1 \sim N$，因为他们对答案没有任何影响。然后那个 $\sum_{p=1}^l(p-1)$ 即枚举 $p$（与 $l+1$ 位置重复的点），那么答案是 $p-1$，累加求和。而第一步化成第二步用到了等差数列求和。

所以我们只需要枚举 $l$ 把 $A_{n-1}^{l-1}\times N^{N-l}\times {l(l-1) \over 2}$ 这个玩意儿求和即可。

最后提醒：记得取模 $M$ 。

代码

#include <bits/stdc++.h>
#define L(i, a, b) for(int i = a; i <= b; i++)
#define R(i, a, b) for(int i = a; i >= b; i--)
using namespace std;
const int N = 1e6 + 10;
int n, m, a = 1, ans, pn[N];
int main(){
    scanf("%d%d", &n, &m);
    pn[0] = 1;
    L(i, 1, n){
        pn[i] = 1ll * pn[i - 1] * n % m;//预处理n的i次方
    }
    L(l, 1, n){
        ans = (ans + 1ll * a * pn[n - l] % m * (1ll * l * (l - 1) / 2 % m) % m) % m;//按照上面的公式累加进答案
        a = 1ll * a * (n - l) % m;//算组合数
    }
    printf("%lld\n", 1ll * ans * n % m);//有n行，所以乘n
    return 0;
}