Trie树入门
孔子有言“温故而知新”,由于近期复习了 $trie$ 树的基本知识点,来写篇对他的总结。
处理的问题
$trie$ 树经常用于处理一类字符串问题,比如他可以查询当前字符串是否在字典中出现过、可以得知每个字符串有多少个前缀或者后缀、是 $AC$ 自动机的一部分等等。待会后面还会讲到一个 $01-trie$ ,他就可以用来处理整数位运算类的问题。
其实 $trie$ 树不像线段树,虽然说他们处理的都是同一类问题,但是 $trie$ 树实际上比线段树好实现,而且变化没有太大,固定的板子是不变的,只是在上面用其它数组简单维护一些东西,不得不说 $trie$ 树只是一种在处理问题过程中的一小步吧。不过有时候正是因为有了 $trie$ 树才能完成问题的转化,从而简化问题。
步骤
大体的板子的步骤其实非常简单,在这就提一嘴罢:
- 初始化 $trie$ 树(谨防多侧),把表示节点个数的 $tot$ 和表示边的 $t$ 数组全部清零,我们可以认为 $0$ 号节点存在,是第一个节点,有他指向字符串里的第一个字符。
- $Insert$ 函数,进行插入,从根节点开始访问,按照当前字符串里的字符作为边的值指向子节点,如果没有,则动态新建一个
- $Query$ 函数,进行查询,总体的遍历方式和插入一样,只是过程中不要新建节点,而且要在函数中维护要查询的东西即可。
再单独列出 $trie$ 树的注意点:
-
根节点是一个空节点
一定要给根节点留出位置
-
采取动态开点方式
如果当前节点已经有当前串下一个位置的字符这个儿子,那么就不用建立,否则要建立一个新的儿子。
可以借助此图理解理解(一张高清大图):
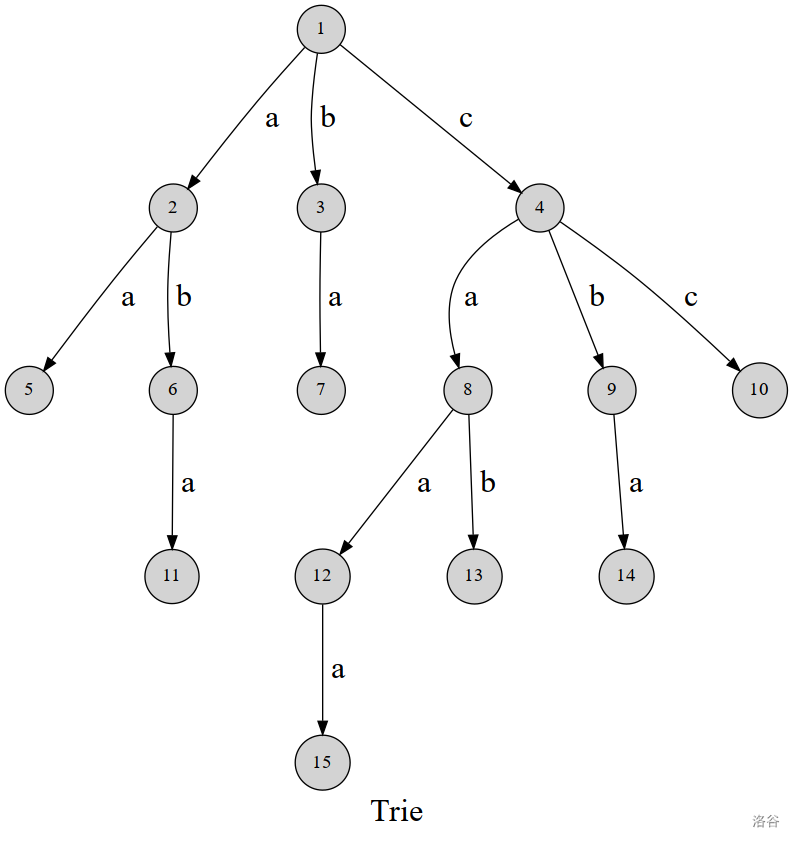
$01-trie$
$01-trie$ 是一种可以处理整数位运算的 $trie$ 树。 $01-trie$ 本质和 $trie$ 没区别,因为他和 $trie$ 树一样很简单。他就是把整数变成二进制串(不足位补 $0$),然后再按 $trie$ 树有水有老的套路去处理。其所维护者与 $trie$ 大同小异,但是 $01-trie$ 很多时候会有一个优先级:比如说遍历 $0$ 的边和遍历 $1$ 的边那个能让得到的值更怎么样,那么会优先遍历当前最优的边,之所以这样做是因为我们知道不管是二进制也好,十进制也好, $n$ 进制也好,他们都是优先满足高位的。
例题
选了 $2$ 题例题。
T1
题意: 给定一棵 $n$ 个点的带权树,求树上最长的异或和路径。
题解: 随便指定一个 $root$ ,然后算出从 $root$ 出发到所有节点的异或和。我们再设 $T(u,v)$ 为 $u$ 到 $v$ 路径上的异或和,那么可得:$T(u,v)=T(root,u) \bigoplus T(root,v)$, 因为从他们的最近公共祖先到根的异或和抵消了。
之后我们利用 $01-trie$ 水过即可。
这道题本质是一个性质及 $01-trie$ 导致模型的转换,使得问题变简单。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#define L(i, a, b) for(int i = a; i <= b; i++)
#define R(i, a, b) for(int i = a; i >= b; i--)
using namespace std;
const int N = 1e6 + 10;
struct A{
int v, w;
};
int n, val[N], mx;
vector<A> g[N];
struct Trie{
int t[N * 2][2], tot;
void Init(){
tot = 0;
memset(t, 0, sizeof(t));
}
void Insert(int x){
int p = 0;
R(i, 30, 0){
int now = (bool)(x & (1 << i));
if(!t[p][now])
t[p][now] = ++tot;
p = t[p][now];
}
}
int Query(int x){
int p = 0, sum = 0;
R(i, 30, 0){
int now = (bool)(x & (1 << i));
if(t[p][now ^ 1])
p = t[p][now ^ 1], sum += 1 << i;
else
p = t[p][now];
}
return sum;
}
} t;
void dfs(int x, int p){
t.Insert(val[x]);
mx = max(mx, t.Query(val[x]));
for(A e: g[x]){
int v = e.v, w = e.w;
if(v == p) continue;
val[v] = w ^ val[x];
dfs(v, x);
}
}
int main(){
while(~scanf("%d", &n)){
mx = 0, t.Init();
L(i, 1, n) g[i].clear();
L(i, 1, n - 1){
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
g[u].push_back((A){v, w});
g[v].push_back((A){u, w});
}
val[1] = 0;
dfs(1, 0);
printf("%d\n", mx);
}
return 0;
}T2
POJ2513——道巨水的题。 这里之所以要拿出来,是因为它是通过trie树进行模型转换的一个代表。 那我们
题意:给你一些木棍,木棍首尾分别各有一个单词,请将所有木棍排成一行,使得任意相邻的木棍相接处的单词一样。
题解:我们把单词插入字典树中变成数字编号,不难发现木棍变成了边,数字编号是点的编号,因为是一条而不是一个环,我们只要求是否存在欧拉通路即可。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#define L(i, a, b) for(int i = a; i <= b; i++)
#define R(i, a, b) for(int i = a; i >= b; i--)
using namespace std;
const int N = 500010;
int n, m, d[N];
pair<int, int> e[N];
struct Trie{
int tot, c[N], trie[N][26];
int Insert(char *s){
int p = 0, l = strlen(s);
if(s[l - 1] == '\n') l--;
L(i, 0, l - 1){
int v = s[i] - '0';
if(!trie[p][v]) trie[p][v] = ++tot;
p = trie[p][v];
}
if(!c[p]) c[p] = ++n;
return c[p];
}
} t;
struct DSU{
int fa[N];
void Init(){
L(i, 1, n) fa[i] = i;
}
int Find(int x){
return x == fa[x]? x : fa[x] = Find(fa[x]);
}
void Union(int x, int y){
x = Find(x), y = Find(y);
fa[x] = y;
}
} dsu;
int main(){
char s[23], a[12], b[12];
while(fgets(s, 23, stdin) != NULL){
sscanf(s, "%s %s", a, b);
e[++m] = make_pair(t.Insert(a), t.Insert(b));
}
dsu.Init();
L(i, 1, m){
dsu.Union(e[i].first, e[i].second);
d[e[i].first]++, d[e[i].second]++;
}
int cnt = 0;
L(i, 1, n){
if(dsu.Find(i) != dsu.Find(1)){
puts("Impossible");
return 0;
}
if(d[i] & 1) cnt++;
}
if(!cnt || cnt == 2){
puts("Possible");
}
else{
puts("Impossible");
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号