CF1783E 题解

这道题目是个水题，然后还是没能独立做出……

题意

因为有中文了，所以就不再赘述。

这里罗列翻译两个不太清晰的点（只是个人认为）：

1. 每一个 boss 是独立的，和上一个怪物没有关系。
2. 每个人的 $k$ 次只是对于自己，不算入对方的计数里面。

解题思路

先进行转换，题意是求所有满足 $\lceil \frac{a_i}{k} \rceil \leq\lceil \frac{b_i}{k} \rceil$ 。

不难想到用最基础的容斥：拿总数 $n$ 减去不合法的 $k$ 就是合法的 $k$ ，非不合法的就是合法的。那接下来又该怎么求呢？既然上面说怪物之间两两独立，不妨先单独考虑。

对于当前 $a_i,b_i$ ，不合法的 $k$ 有哪些呢？那我们可以再假设我们已经确定了 $k$ ，要判定他在当前 boss 这里合不合法，只需要判断 $k$ 有没有倍数处于 $[b_i,a_i-1]$ 这个区间即可，如果有的话是显而易见，可以直观的看这张图：

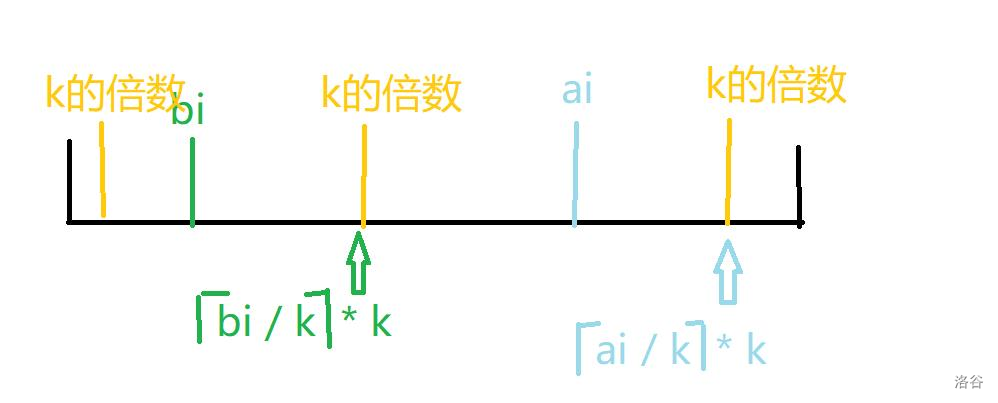
反之同理，对于这个 boss 来说当前 $k$ 是合法的。所以对于一个 boss 来说合法的是在 $[b_i,a_i-1]$ 区间中没有他的倍数的数。

那么我们对于所有 boss 只需要枚举他在所有的 $[b_i,a_i-1]$ 中有没有他的倍数即可。

时空复杂度

时间复杂度 $O(n \log n)$ ，为调和级数，是在枚举 $1$ 到 $n$ 中所有数的倍数时所用的时间花销，由于所有 $n$ 之和不超过 $2*10^5$ ，然后每组数据带的 $log$ 一定是小于 $\log n$ 的，所以时间复杂度不超过 $n \log n$ 。

空间复杂度 $O(n)$ 。

自我总结

这道题目没有做出来是不应该的，第一步基础容斥想到了，分开考虑也想到过，但是之后就没有朝着正解前进了。

所以主要还是没有发现最后的结论，以后可以画个数轴方便自己思考题目。

代码

#include <bits/stdc++.h>
#define L(i, a, b) for(int i = a; i <= b; i++)
#define R(i, a, b) for(int i = a; i >= b; i--) 
using namespace std;
const int N = 2e5 + 10;
int T, n, cnt, a[N], b[N], t[N], f[N];
void Solve(){
    scanf("%d", &n), cnt = 0;
    L(i, 1, n) scanf("%d", &a[i]), t[i] = 0;
    L(i, 1, n){
        scanf("%d", &b[i]);
        if(a[i] > b[i]) t[b[i]]++, t[a[i]]--;
    }
    L(i, 1, n) t[i] += t[i - 1];
    L(i, 1, n){
        int flag = 0; f[i] = 1;
        L(j, 1, n / i) 
            if(t[i * j]){f[i] = 0; break;}
        cnt += f[i];
    }
    printf("%d\n", cnt);
    L(i, 1, n)
        if(f[i]) printf("%d ", i);
    putchar('\n');
}
int main(){
    scanf("%d", &T);
    while(T--) Solve();
    return 0;
}