CF1779E 题解

这是我的第一道交互题。

然后挂了好久，错误的改正如下：

• 每个输入或者输出完就要一句 fflush(stdout);。
• 询问的时候对于 $i$ 号点不要把第 $i$ 位置 $1$，不然的话会答案错误（因为自己和自己对决测评机不知该如何回答你）。

思路

首先，我们先来明确一个定义：竞赛图。对于这道题目，我们如果把节点两两之间连一条有向边，由这两个节点比赛的胜者指向败者，那么会形成一张任意两个节点之间有且仅有一条有向边的竞赛图。

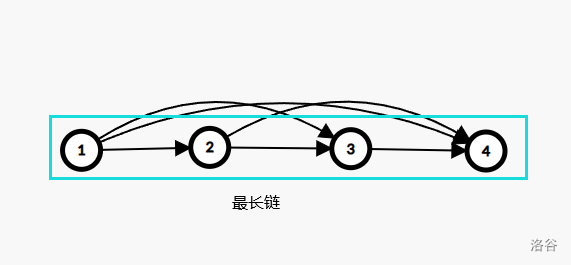
• 结论 $1$：假设已经知道了连边情况，我们把竞赛图进行强联通缩点，那么得到的有向无环图中每个节点会向自己后面的节点连边。严谨地说，有向无环图的最长链的节点个数等于这个图的节点个数，且最长链上的节点每个朝着自己后面的所有节点连边。

  

• 证明 $1$：这个不难，我们发现假设有后面的点连向前面的话，必定会再构成一个更大的强联通分量，所以必定是前面的节点只想后面，而因为原图两两之间有连边，所以新图的两个点之间也有连边，所以就成了图上见到的样子。

• 结论 $2$：原图中每个点会向新图中所处的强联通分量之后的强联通分量的所有点连边。

  其实有点绕，那就比如说上面的那张图的 $3$ 号强联通分量在原图中的点会向上面的 $4$ 强联通分量在原图中的点连边。

• 证明 $2$：因为两两之间有连边，不是你连我就是我连你，如果前面的强联通分量中的点不连向后面的强联通分量中的点，那么就是后面连前面，那就成环了，然而我们知道缩点后不存在环，所以得证。

• 结论 $3$：对于这个有向无环图的唯一入度为 $0$ 的节点，即拓扑序最小的节点、上图中的 $1$ 号点，他里面的所有节点就是答案。

• 证明 $3$：这个显而易见，因为 $1$ 中的所有节点是可以互达的，也就意味着任意一个节点可以通过其他人打败 $1$ 中的所有人。那么再考虑后面的强联通分量，前面的可以通过边打败后面的是显然，而后面的也没有途径能打败前面的（因为没有连向前面的边）。

• 结论 $4$：前面的强联通分量的点的出度严格大于后面强联通分量的点的出度。

• 证明 $4$：因为前面的点指向后面的所有点，他的出度大于等于后面点的个数；后面的点会向除自己以外更后面的点连边，所以会严格小于前面的点的出度。

那么我们通过 $n-1$ 次询问得知前 $n-1$ 个点的出度（设 $i$ 号点的出度为 $d[i]$），最后一个点的出度可以拿总出度 $n \times (n-1)/2$ 减去前 $n-1$ 个点的出度和得到，即 $d[n] = n \times (n-1)/2 - \sum_{i=1}^{n-1}d[i]$。我们按照 $d$ 数组的值从大到小对每个点排序，那么又有：

• 结论：最终答案一定是以有序数组的前缀的形式出现。
• 证明：因为第一个的强联通分量中的点（即所有满足条件的点）出度大于后面的所有点，具体可以看上述的结轮 $4$。

而我们又怎么求哪一段前缀是答案呢？不妨假点 $u$ 排序后处在 $i$ 个位置，那么可知前 $i$ 个点之间两两连边对出度的贡献和是 $i \times (i-1)/2$，而前 $i$ 个点总共的出度表示为 $\sum_{j=1}^id[j]$，又可知前 $i$ 个点向后面的 $n-i$ 个点连边产生的出度和为 $\sum_{j=1}^id[j]-i \times (i-1)/2$，于是排序后的 $1$ 号位置到第一个满足 $\sum_{j=1}^id[j]-i \times (i-1)/2 = i \times (n-i)$ 的位置这段区间的节点即为答案。

我们思考怎么证明。首先，答案存在这点不可否认。那么，通过结论 $2$，我们知道了对于可能回获胜的点（即答案）来说，每个点向后面的强联通分量所连出去的边的出度和为 $n-i$，也就是后面的点数，那么前面有 $i$ 个点，所以满足每个点都想后面的所有点连边也就要满足上面一段中的那个式子。

其次，第一个强联通分量必定是第一个满足上面式子的。我们可以利用反证法证明，假设强联通分量内部少了一些点却依旧满足上式，那么又有这是一个强联通分量，每个点一定会有连向强联通分量内部其他点的边，而由于假设里面选择的那些点根据性质 $2$ 会向剩下每个点都连一条边，那就根本不可能组成一个强联通分量，故得证。

#include <bits/stdc++.h>
#define L(i, a, b) for(int i = a; i <= b; i++)
#define R(i, a, b) for(int i = a; i >= b; i--)
using namespace std;
const int N = 251;
int n, sum, id[N], d[N], ans[N];
char s[N];
bool cmp(int i, int j){return d[i] > d[j];}
int main(){
    scanf("%d", &n);
    fflush(stdout);
    L(i, 1, n) id[i] = i, s[i] = '1';
    L(i, 1, n){
        if(i == n) d[i] = n * (n - 1) / 2 - sum;
        else{
            s[i] = '0';
            printf("? %d %s\n", i, s + 1);
            s[i] = '1';
            fflush(stdout);
            scanf("%d", &d[i]), sum += d[i];
            fflush(stdout);
        }
    }
    sort(id + 1, id + n + 1, cmp);
    sum = 0;
    L(i, 1, n){
        sum += d[id[i]];
        if(sum - i * (i - 1) / 2 == i * (n - i)){
            putchar('!'), putchar(' ');
            L(j, 1, i) ans[id[j]] = 1;
            L(j, 1, n) putchar(ans[j] + '0');
            fflush(stdout);
            return 0;
        }
    }
    return 0;
}