CF835F 题解

前言

双倍经验题。按我的做法本题答案除以 $2$ 就能通过那道题。

这是一题基环树入门题，很套路。就是把基环树转到序列上乱搞一通就过了。

思路

基环树转到序列上过于套路，没啥可讲的，就讲一下序列上则怎么处理吧。

我们假设现在已经转到了序列上（不用把序列复制一遍，而是直接处理），我们枚举断边，那么可以观察到现在被分为了两边——当前断边断开的左边和右边，我们可以预处理出 $mx1$ 表示当前以及当前左边的所有节点子树，这些节点中的最远距离，即维护前缀最远距离。$mx2$ 乃反之，亦然，为后缀最远距离。

我们发现可能会存在最远点对中一个在左边，一个在右边，那么我们就维护一个 $mxq$ 表示当前的前缀距离（当前点到序列最前面点的距离）加上当前子树内的最大深度节点，$mxh$ 与其堆成，表示当前的后缀距离（当前点到序列最后面点的距离）加上当前子树内的最大深度节点。

可以借助下图进行理解：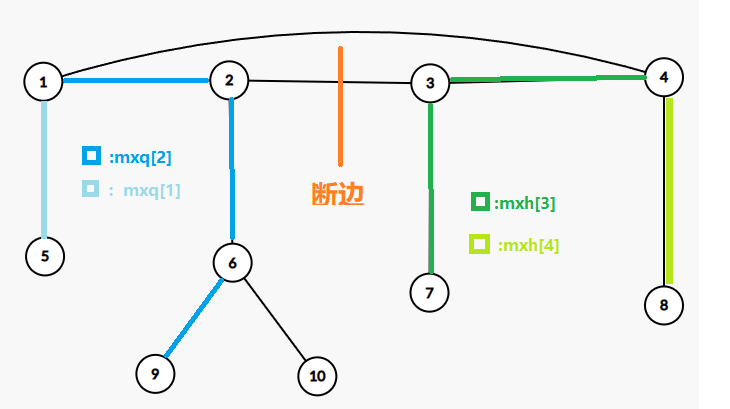

所以每次取 $mx1_i$、$mx2_{i+1}$ 与 $mxq_i+mxh_{i+1}+\text{连接序列首尾两点的那条边}$ 的最大值作为断当前边的直径，那么拿所有断边的直径取最小值就是答案。

坑点提醒：

• 直径可能存在于单个环上节点的子树内。
• 只能删环上的边，因为删完要保持连通。

代码。