[APIO2023] 赛博乐园 题解

方法 $1$：分层图 SPFA

$97$ 分做法

一个分层图 SPFA，直接对模板改改就行了。

具体的，状态 $d_{u,i}$ 表示走到 $u$ 这个节点，用了 $i$ 次“除以 $2$ 的能力”所花费的最少时间。同时，这道题的 SPFA 转移多了一种：对于一条边 $u$ 到 $v$ 权值为 $w$ 的边，若 $a_v=2$，那么拿 $\frac{(d_{u,i}+w)}{2} \to d_{v,i+1}$。

中途若拓展到 $a_u=0$ 的点，直接 $d_{u,i}=0$。

$100$ 分做法

只需要把 $k$ 和 $70$ 取个 $\min$ 就行了。

证明：考虑假设有一条路径上有超过 $70$ 个位置用了“除以 $2$ 的能力”，会发现前面的所有的“除以 $2$ 的能力”现在都不用了，只保留最后 $70$ 次也能使精度误差在 $10^{-6}$ 以内。考虑只保留后 $70$ 次的方案中的第一次除以 $2$ 前的那条路径，总时间不会超过 $n \times v$，$v$ 表示通过一条路的最大时间，所以不超过 $10^5 \times 10^9=10^{14}$。

如下图：

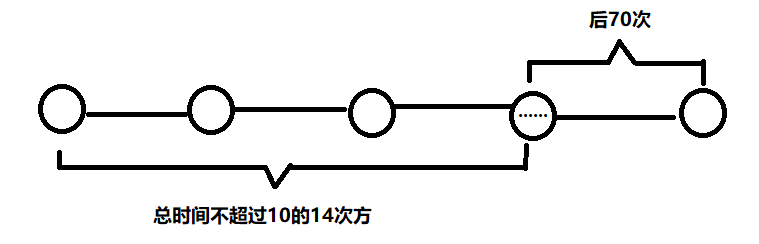
在后面的 $70$ 次除以 $2$ 便能把前面那一个极端的数给除到 $10^{-6}$ 以下。

代码

注意点：

• 多测清空。
• 途中不能经过 $h$。

以下代码使用了 SPFA 的 SLF 优化。

#include <bits/stdc++.h>
#define ll long long
#define db double
#define L(i, a, b) for(int i = (a); i <= (b); i++)
#define R(i, a, b) for(int i = (a); i >= (b); i--)
using namespace std;
const int N = 1e5 + 10, K = 71;
struct E{int v, w;};
struct Node{int u, t;};
int n, m, k, h, a[N], vis[N][K];
db ans, d[N][K];
vector<E> g[N];
deque<Node> q;
void spfa(){
    L(i, 1, n) L(j, 0, k) d[i][j] = 1e18, vis[i][j] = 0;
    L(j, 0, k) vis[h][j] = 1;
    while(!q.empty()) q.pop_front();
    d[1][0] = 0; q.push_back({1, 0}), vis[1][0] = 1;
    while(!q.empty()){
        int u = q.front().u, t = q.front().t;
        q.pop_front(), vis[u][t] = 0;
        for(auto &e: g[u]){
            int v = e.v, w = e.w;
            if(t < k && a[v] == 2 && d[u][t] + w < d[v][t + 1] * 2){
                d[v][t + 1] = (d[u][t] + w) / 2.0;
                if(!vis[v][t + 1]){
                    if(!q.empty() && d[v][t + 1] < d[q.front().u][q.front().t])
                        q.push_front({v, t + 1});
                    else q.push_back({v, t + 1});
                    vis[v][t + 1] = 1;
                }
            }
            if(d[u][t] + w < d[v][t]){
                d[v][t] = d[u][t] + w;
                if(!a[v]) d[v][t] = 0;
                if(!vis[v][t]){
                    if(!q.empty() && d[v][t] < d[q.front().u][q.front().t])
                        q.push_front({v, t});
                    else q.push_back({v, t});
                    vis[v][t] = 1;
                }
            }
        }
    }
}
double solve(int N, int M, int K, int H, vector<int> X, vector<int> Y, vector<int> C, vector<int> ARR){
    n = N; m = M; k = min(K, 70); h = H + 1; ans = 1e18;
    L(i, 1, n) a[i] = ARR[i - 1], g[i].clear();
    L(i, 0, m - 1){
        int u = X[i] + 1, v = Y[i] + 1, w = C[i];
        g[u].emplace_back((E){v, w}), g[v].emplace_back((E){u, w});
    }
    spfa();
    L(j, 0, k) ans = min(ans, d[h][j]);
    return ans == 1e18? -1 : ans;
}

方法 $2$：分层图 Dijkstra

解题思路

我们知道对于一条边，它最终的贡献取决于它的权值以及经过它之后使用的“除以 $2$ 的能力”次数。又由于是无向图，所以考虑倒着 Dijkstra，分层图的状态设计和 SPFA 的一样。这样就可以知道每条边后面使用了多少次“除以 $2$ 的能力”。特别的，若遇到 $a_u=0$ 的点，直接让“除以 $2$ 的能力”使用次数变成 $70$，那样的话就能巧妙的在一定的误差内处理。

代码

#include <bits/stdc++.h>
#define ll long long
#define db double
#define L(i, a, b) for(int i = (a); i <= (b); i++)
#define R(i, a, b) for(int i = (a); i >= (b); i--)
using namespace std;
const int N = 1e5 + 10, K = 72;
struct E{int v, w;};
int n, m, k, h, a[N], vis[N][K];
db ans, d[N][K], pw[K];
vector<E> g[N];
struct Node{
    int u, t; db d;
    bool operator < (const Node &cmp)const{return d > cmp.d;}
};
priority_queue<Node> q;
void Dijkstra(){
    L(i, 1, n) L(j, 0, 70) vis[i][j] = 0, d[i][j] = 1e18;
    while(!q.empty()) q.pop();
    q.push({h, 0, d[h][0] = 0});
    while(!q.empty()){
        int u = q.top().u, t = q.top().t;
        q.pop();
        if(vis[u][t]) continue;
        vis[u][t] = 1;
        for(auto &e: g[u]){
            int v = e.v, w = e.w; if(v == h) continue;
            if(!a[v]){
                if(d[u][t] + w * pw[t] < d[v][70])
                    q.push({v, 70, d[v][70] = d[u][t] + w * pw[t]});
            }
            else if(t < k && a[v] == 2){
                if(d[u][t] + w * pw[t] < d[v][t + 1])
                    q.push({v, t + 1, d[v][t + 1] = d[u][t] + w * pw[t]});
            }
            else{
                if(d[u][t] + w * pw[t] < d[v][t])
                    q.push({v, t, d[v][t] = d[u][t] + w * pw[t]});
            }
        }
    }
}
double solve(int N, int M, int K, int H, vector<int> X, vector<int> Y, vector<int> C, vector<int> ARR){
    n = N; m = M; k = min(K, 70); h = H + 1; ans = 1e18;
    L(i, 1, n) a[i] = ARR[i - 1], g[i].clear();
    pw[0] = 1; L(i, 1, 70) pw[i] = pw[i - 1] / 2;
    L(i, 0, m - 1){
        int u = X[i] + 1, v = Y[i] + 1, w = C[i];
        g[u].emplace_back((E){v, w}), g[v].emplace_back((E){u, w});
    }
    Dijkstra();
    L(i, 0, 70) ans = min(ans, d[1][i]);
    return ans == 1e18? -1 : ans;
}