P1791 [国家集训队] 人员雇佣

考虑最小割。不妨把问题简化成两个人去看。根据最小割建模的套路，易画出类似这样的图：

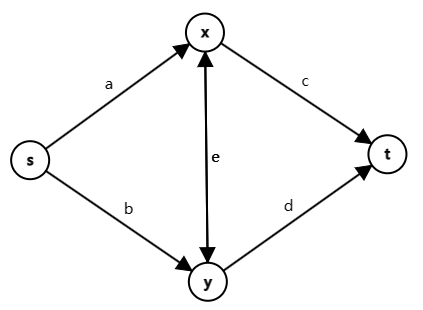
其中，$s,t$ 分别为源汇点，$x,y$ 均各自代表了一个经理。最小割中，割掉 $a$ 看作雇佣了 $x$，割掉 $c$ 看作不雇佣 $x$，$y$ 同理。

发现图中还有一个 $e$。我们割掉 $e$ 当且仅当 $x,y$ 中恰好有一个经理被雇佣了，也就是说，$e$ 能把 $x,y$ 恰好选一个所带来的负向利润减去。

考虑先把答案加上 $\sum_{x=1}^n\sum_{y=1}^nE_{x,y}$，之后再用最小割减去花费以及必须舍弃的利润得到答案。

其实到了这一步，$a,b,c,d,e$ 的值应该是已经比较明了了。但是下面介绍一种比较暴力的方式：

会发现不同的情况对图中 $a,b,c,d,e$ 五个变量组成了如下限制：

• 情况 $1$：$x,y$ 经理都被雇佣了$$ a+b=A_x+A_y $$

• 情况 $2$：$x$ 经理被雇佣，$y$ 经理没被雇佣$$ a+d+e=A_x+3E_{x,y} $$

• 情况 $3$：$x$ 经理没被雇佣，$y$ 经理被雇佣$$ b+c+e=A_y+3E_{x,y} $$

• 情况 $4$：$x,y$ 经理都没被雇佣$$ c+d=2E_{x,y} $$

  $(2)+(3)-(1)-(4)$ 得到 $e=2E_{x,y}$。

  $a,b,c,d$ 也不难得出一组合法解：

  $$ a=A_x $$$$ b=A_y $$$$ c=E_{x,y} $$$$ d=E_{x,y} $$

上述是两个经理的情况，多个经理也类似，这里就不赘述了。

#include <bits/stdc++.h>
#define FL(i, a, b) for(int i = (a); i <= (b); i++)
#define FR(i, a, b) for(int i = (a); i >= (b); i--)
using namespace std;
typedef long long ll;
const int N = 1010, M = 1002010;
const ll INF = 1e18;
struct E{int v; ll w, nxt;} e[M << 1]; ll ans;
int n, m, s, t, tote, a[N], c[N][N], head[N], now[N], dep[N];
void init(){
    tote = 0;
    memset(head, -1, sizeof(head));
}
void Adde(int u, int v, ll w){
    e[tote] = {v, w, head[u]}, head[u] = tote++;
}
void Add(int u, int v, ll w){
    Adde(u, v, w), Adde(v, u, 0);
}
int bfs(){
    queue<int> q; q.push(s);
    memset(dep, 0, sizeof(dep)), dep[s] = 1;
    while(!q.empty()){
        int u = q.front(); q.pop();
        for(int i = now[u] = head[u]; ~i; i = e[i].nxt)
            if(e[i].w && !dep[e[i].v])
                q.push(e[i].v), dep[e[i].v] = dep[u] + 1;
    }
    return dep[t];
}
ll dfs(int u, ll in){
    if(u == t) return in; ll out = 0;
    for(int i = now[u]; ~i && in; i = e[i].nxt){
        int v = e[i].v; ll w = e[i].w; now[u] = i;
        if(dep[v] == dep[u] + 1 && w){
            ll flow = dfs(v, min(in, (ll)w));
            in -= flow, out += flow;
            e[i].w -= flow, e[i ^ 1].w += flow;
        }
    }
    if(!out) dep[u] = 0; return out;
}
ll dinic(){
    ll ret = 0;
    while(bfs()) ret += dfs(s, INF);
    return ret;
}
int main(){
    scanf("%d", &n), s = 0, t = n + 1, init();
    FL(i, 1, n) scanf("%d", &a[i]), Add(s, i, a[i]);
    FL(i, 1, n){
        ll sum = 0;
        FL(j, 1, n){
            scanf("%d", &c[i][j]);
            if(c[i][j] > 0){
                Add(i, j, 2 * c[i][j]);
                sum += c[i][j];
            }
        }
        Add(i, t, sum), ans += sum;
    }
    printf("%lld\n", ans - dinic());
    return 0;
}