算法学步：回溯法-8皇后问题

问题描述：

有八个皇后（可以当成八个棋子），如何在 8*8 的棋盘中放置八个皇后，使得任意两个皇后都不在同一条横线、纵线或者斜线上

 

 

 

 

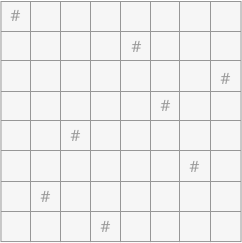
做法：

从第一行开始，一行一行地考虑，这样起码可以保证皇后不在同一行；

考虑下面的每一行的时候，需要让新增加的棋子不在前面添加的棋子的左下、正下、右下，即新增加的棋子的列不等于前面棋子的列，它的行号+列号不等于前面棋子的行号加列号（不在左下），|行号-列号|不等于之前棋子的|行号-列号|（不在右下）；

如果该行所有位置都不符合要求，则回溯到前一行，改变皇后的位置，继续试探；

如果试探到最后一行，所有皇后摆放完毕，则直接打印出 8*8 的棋盘。最后一定要记得将棋盘恢复原样，避免影响下一次摆放。

以四皇后问题为例，考虑一棵树（图片来自水印）

 

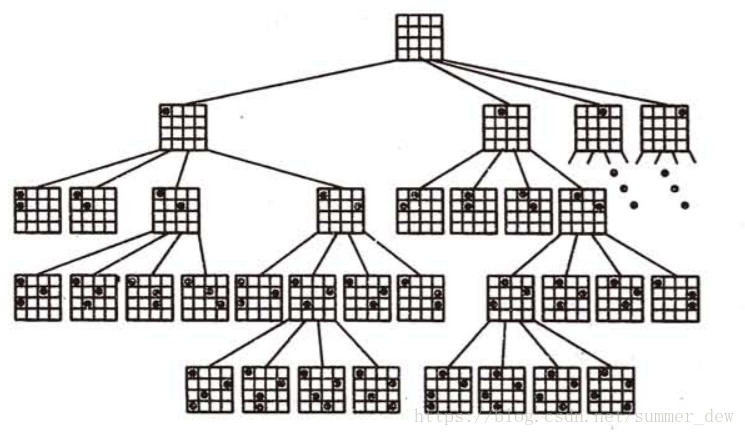
 树的深度表示考虑棋盘的行数，树深度为1表示考虑棋盘的第一行等等，每个节点表示棋盘的一个状态，节点的子节点表示在一个棋盘状态下考虑棋盘的下一行的棋子摆放状态，同一深度的节点从左到右分别表示棋子摆放在这一行的不同位置（列）上；

树的遍历顺序为向下👇和向右👉，

开始时深度优先遍历这棵树，如果能到达叶节点，则说明棋盘的所有行都按要求放上了棋子，即找到了一个可行解，因为一共就4列，所以此时每一列都有棋子了，挪动第四行的棋子必然会导致两个棋子出现在同一列，因此无法通过访问可行解的兄弟节点再得到可行解，此时应返回上一行，挪动上一行棋子的位置；

若某一行所有位置均不可行，则返回上一行，向右挪动棋子的位置，即访问父节点的右兄弟节点，最终函数再根节点返回，算法结束。

程序代码：

/*回溯法，8皇后问题*/
#include<stdio.h>
#include<iostream>
#include<cmath>
#include<math.h>
using namespace std;
int weizhi[8]={0};//用来保存八个棋子的位置
int counts=0;
bool check(int hang, int lie);
void Queens(int nhang);
void print();
int main()
{
    Queens(0);
    cout<<"8皇后问题的解的个数为:"<<counts<<endl;
    return 0;
}

int Check(int line,int list){
    //遍历该行之前的所有行
    for (int index=0; index<line; index++) {
        //挨个取出前面行中皇后所在位置的列坐标
        int data=weizhi[index];
        //如果在同一列，该位置不能放
        if (list==data) {
            return 0;
        }
        //如果当前位置的斜上方有皇后，在一条斜线上，也不行
        if ((index+data)==(line+list)) {
            return 0;
        }
        //如果当前位置的斜下方有皇后，在一条斜线上，也不行
        if ((index-data)==(line-list)) {
            return 0;
        }
    }
    //如果以上情况都不是，当前位置就可以放皇后
    return 1;
}
//blog.csdn.net/yuer_xiao/article/details/82714734
void Queens(int nhang)//考虑第n行的棋子放置问题
{
    for(int lie=0;lie<8;lie++)
    {
        if(Check(nhang,lie))
        {
            weizhi[nhang]=lie;
            if(nhang==7)
            {
                counts+=1;
                print();
                weizhi[nhang]=0;
                return;
            }
            Queens(nhang+1);
            weizhi[nhang]=0;
        }
    }
    return;//考虑完全部8个位置，没有符合要求的，返回上一行调用Queens(nhang+1)的地方，使上一行的位置数+1，其实此处不用写return，执行完成之后
}

void print()
{
    for (int line = 0; line < 8; line++)
    {
        int list;
        for (list = 0; list < weizhi[line]; list++)
            printf("0");
        printf("#");
        for (list = weizhi[line] + 1; list < 8; list++){
            printf("0");
        }
        printf("\n");
    }
    printf("================\n");
}