[算法][几何计算]覆盖最多点固定半径圆问题 最多覆盖圆 圆的扫描线 详细解法 [POJ1981]

引题： 覆盖最多点固定半径圆问题

背景：

在二维平面中给定n个点，求半径为r的圆最多可以覆盖多少个点（1 <= n <= 300, 精度eps = 0.0001）

输入：

第一行两个数，整数n代表点的个数，浮点数r代表圆的半径。以下第i + 1行(1 <= i <= n) 输入第i个点的两个浮点数x、y，表示第i个点的坐标

输出：

一个整型，表示点的个数

样例：

Input:

4 1.0

1 1

2 2

2.7 2.7

3 2.5

Output：

3

 

改编自POJ1981 Circle and Point

相比于原题，追加了可以定义半径r，以及求出覆盖最多点圆中的一个合理圆心。

---

 

思路一：暴力枚举 时间复杂程度O(n³)

思路：

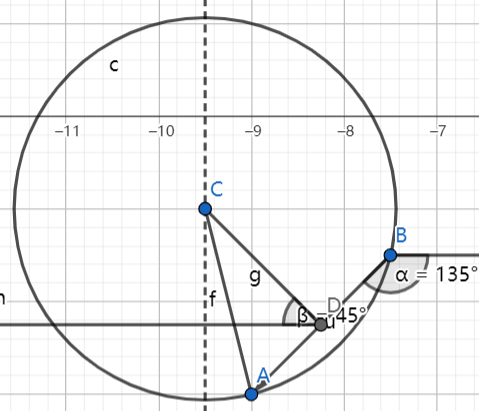
枚举两个点，求出这两个点在以r为半径的圆的圆弧上的两个圆心（这两个圆心以这两个点的连线为对称轴对称）（实际上每次循环只需要求出其中一个就行了，因为二重循环中总会枚举出这两个圆心，比如说在i = 1, j = 3和i = 3, j = 1的时候就各枚举出了这两个圆）

如何求出这个圆心？列数学方程就可以了，圆心在两个点的中垂线上，并且距离到两个点的距离都为r，勾股定理求出中点到圆心的距离，然后用atan2求出两个点的极角，减去π/2就是π减去中点与圆心形成向量的极角，然后就可以计算出圆心的坐标了。假设这两个点的极角为α = atan2(y₂-y₁, x₂-x₁)，中点坐标为(x₀,y₀)，圆心坐标为(x_c,y_c)，圆心到中点的距离为d，则可以得到：

x_c=x₀ + dsinα

y_c=y₀ - dcosα

然后再求这个圆覆盖点的个数，总时间复杂程度为O(n³)

---

 

思路二：扫描线 时间复杂程度O(n²logn)

优点：时间复杂程度更低

缺点：理解起来比较复杂（其实有高中数学基础的话应该好理解）、写起来比较复杂。如果语言没有排序算法需要自己写一个排序（时间复杂程度取决于这个排序）

思路：

在以任意一个点P为圆心、r为半径的圆所覆盖的区域中取任意一点为圆心、r为半径的圆，这个圆一定过点P。

那么只需要让所有的点都为圆心、建半径为r的圆，求出被覆盖最多的区域，则取这个区域中的任意一点为圆心、半径r的圆为覆盖点最多的圆。

那么可以先枚举任意一点P，来探究这个点为圆心、半径为r的圆与其他点Q为圆心的圆覆盖的情况：

• 首先点P的整个圆都先被记录到被覆盖的区域中，并初始化覆盖点最多的圆的圆心为P、半径为r（如何记录进入和退出该区域在下面会描述）
• 其次就是枚举出任意一个点Q如果相交则有两个点（如果不相交，即两点距离大于2r，则跳过），连接点P与两个交点的话很明显这两条线可以划分为进入这个区域的线和离开这个区域的线。所以我们记录这两条线以及判断它是进入区域的线还是离开区域的线即可。
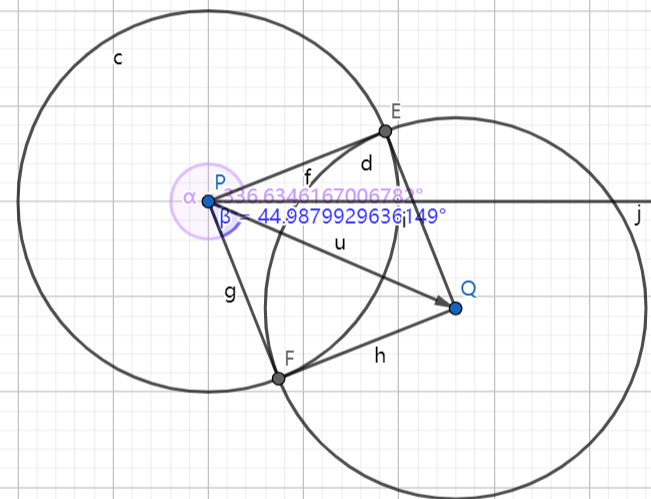
• 这里的一步的难点就在于如何判断这两条线是进入区域和离开区域。首先我们可以根据两个点的坐标和半径就出两个交点的坐标以及点P和两个交点形成向量的极角。
• 如下图中，我们可以得到向量PQ的极角α=atan2(y_Q-y_P,x_Q-x_P)（范围为[-π,π]，图中α应该为336°-360°=-24°），通过余弦定理得出 两个圆心的连线与P点和交点的连线的夹角，设d为两个圆心的距离，则夹角 β = arccos(d / (2 * r))（范围为[0,π]）
• 那么我们就可以求出P与两个交点形成向量的极角 γ=α±β，交点的坐标为(x＋r*cosγ, y+r*sinγ)。我们可以假设极角小的线(γ=α-β)为进入区域的线（图中PF），极角大的线为退出区域的线（图中PE）

 

 

 

•  我们可以求出点P与所有圆交点的极角和极线，根据上方定义极角小的线为进入区域、极角大的线为退出区域，那么我们可以让所有的线根据极角进行从小到大排序。时间复杂程度为O(nlogn)
• 因为还要包括自己整个圆的区域，我们可以让整个圆的起始线的极角为极角的最小值，退出线为的极角为极角的最大值。根据atan2和arccos的范围可以知道，极角的范围为[-2π，2π]，那么可以让起始线的极角等于-2π，退出线为2π
  • 进一步细节：1. 要初始化每个圆所求的答案的圆心为自己的圆心，为什么？2. 由于包含自身肯定是分布在排序的起始和结尾（因为是最小和最大值），我是不是可以不用记录这两个情况直接让最终结果+1？
  • 关于1，如果出现一定区域内一个圆只能覆盖一个点的情况，会因为你没有初始化圆心而找不到这个圆，从而可能会导致各种问题，如死循环
  • 关于2，其实也可以不记录自己的区域、不额外记录这两个极角，只需要让最终答案+1即可；当然你也可以直接初始化答案为1，再相加相减。对于只求覆盖点的个数题来讲，这样做完全没有任何问题
• 另外如果有相切的情况，即两个交点的极角相等，那么我们应该让进入线排在退出线的前面
• 根据排序后的极线来进行判断覆盖点的个数，来对排序后的极线依次扫描：扫描进入线就让覆盖点个数+1，扫描到退出线就让覆盖点个数-1，取这个过程中的最大值就为对于可以覆盖到点P的圆中覆盖点最多的圆。
  • 如果要求圆心，则这个圆心可以是这个极线所对应的交点（因为这个交点一定在这个被覆盖最多次数的这个区域中）
• 对所有的点依次求解，过程中覆盖点的个数的最大值即为答案。枚举所有有点次数为n，则所有的时间复杂程度为O(n²logn)

优化：

• 如果当前交点的个数/2小于目前记录覆盖数最大的值，那么可以直接跳过扫描线的过程。原因也很简单，因为这个区域中最大覆盖点的值就等于交点个数/2，这个区域的最大值都小于目前记录的最大值，则不可能会超过目前记录的最大值。

例子：

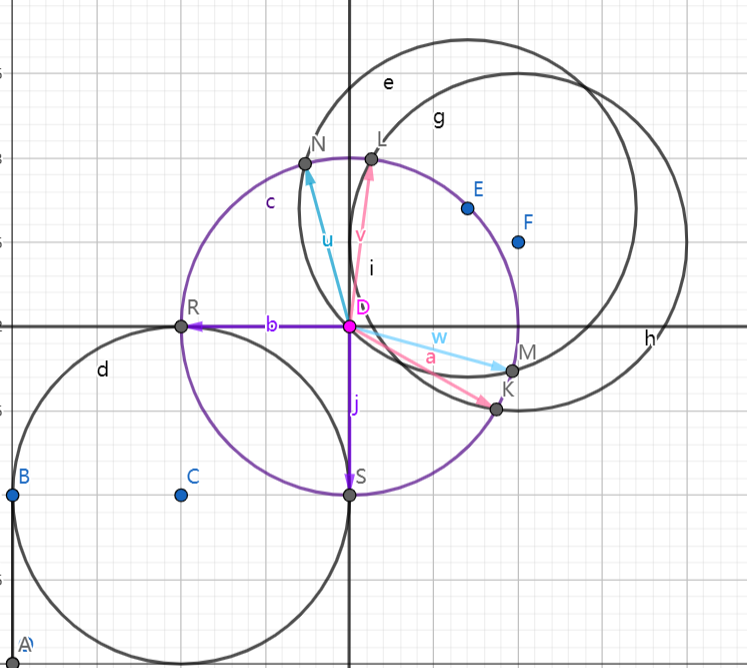
样例中为例，下图中，我们求在以D为圆心半径为1的圆中，与其他所有圆覆盖的情况。（当然除了D以外，还要分别枚举圆E、F、C的情况）

由于D与C的极角是负的，其他为正的，所以所有线中D与C的两个交点形成的向量的极角是最小的（DR与DS，分别为-π和-π/2），所以在左下方三象限这个区域中最大的覆盖数为2。

其次就是D与F和D与E的交点形成向量的极角，很明显顺序为DK、DM、DL、DN，其中DK、DM为进入线，DL和DN为退出线。依次扫描可以知道一二四象限这个区域的覆盖数为3。

取整个过程中覆盖数最大的值，也就是3。

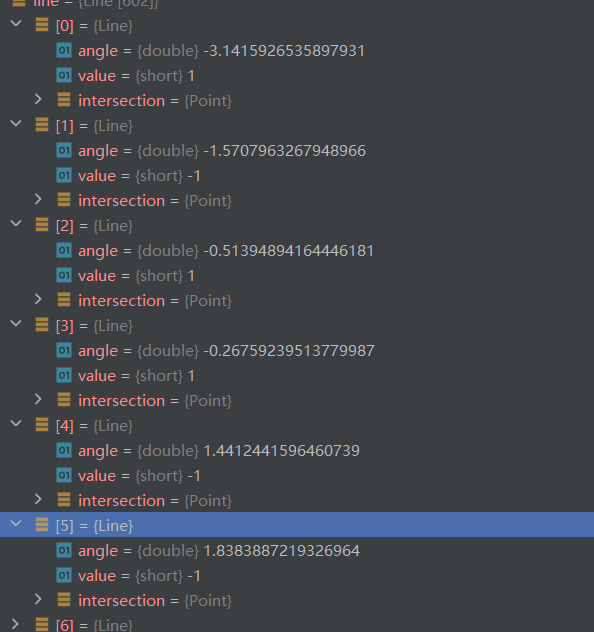
 上图中程序实际跑出的数据（不包括自身，其中1为进入线，-1为退出线）：

 

 

cpp code:

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <utility>
#include <cmath>

#define cout std::cout
#define cin std::cin
#define endl std::endl
#define string std::string

const double eps = 1e-8;
const double pi = acos(-1.0);

int cmpDouble (double x) {
    if (fabs(x) <= eps) return 0;
    return x < 0 ? -1 : 1;
}

struct Point {
    double x, y;
    Point () : x(0.0), y(0.0) {}
    Point (double x, double y) : x(x), y(y){}

    Point operator + (const Point& p) const {
        return {x + p.x, y + p.y};
    }
    Point operator - (const Point& p) const {
        return {x - p.x, y - p.y};
    }
    Point operator * (const double& n) const {
        return {x * n, y * n};
    }
    Point operator / (const double& n) const {
        return {x / n, y / n};
    }
    double operator * (const Point& p) const { // dot product
        return x * p.x + y * p.y;
    }
    double operator ^ (const Point& p) const { // cross product
        return x * p.y - p.x * y;
    }
    bool operator == (const Point& p) const {
        return (cmpDouble(x - p.x) == 0 && cmpDouble(y - p.y) == 0);
    }
    double distance (const Point& p) const { // sqrt( (x2 - x1)^2 + (y2 - y1)^2 )
        return sqrt( (x - p.x) * (x - p.x) + (y - p.y) * (y - p.y) );
    }
    double angle () const {
        return atan2(y, x);
    }
    Point transfer (const double& angle, const double& dist) const {
        return {x + dist * cos(angle), y + dist * sin(angle)};
    }
};
typedef Point Vector;
struct Circle {
    Point center;
    double radius;
    Circle () : center(Point()), radius(0.0) {}
    Circle (Point c, double r) : center(c), radius(r) {}

    bool operator == (const Circle& c) const {
        return center == c.center && cmpDouble(radius - c.radius) == 0;
    }
    bool apart (const Circle& c) const {
        return cmpDouble(center.distance(c.center) - (radius + c.radius)) > 0;
    }
};
struct Scanline {
    Point intersection;
    double polarAngle;
    int value;
    Scanline () : intersection(Point()), polarAngle(0.0), value(0) {}
    bool operator < (const Scanline& l) const { // The smaller angle or greater value comes first
        if (cmpDouble(polarAngle - l.polarAngle) != 0) return polarAngle < l.polarAngle;
        return value > l.value;
    }
};
class resolvent {
private:
    static std::pair < Scanline, Scanline > getScanline (const Circle& a, const Circle& b) {
        Scanline inLine, outLine;
        inLine.value = 1, outLine.value = -1;
        if (a == b) { // Initialization of the same circle
            inLine.polarAngle = -2 * pi;
            inLine.intersection = a.center;
            outLine.polarAngle = 2 * pi;
            outLine.intersection = a.center;
        } else { // two intersections
            Vector AB = b.center - a.center;
            double dist = a.center.distance((b.center));
            double r = a.radius;
            double angleAB = AB.angle();
            double angleAI = acos( dist / (2 * r) );

            inLine.polarAngle = angleAB - angleAI;
            inLine.intersection = a.center.transfer(inLine.polarAngle, r);

            outLine.polarAngle = angleAB + angleAI;
            outLine.intersection = a.center.transfer(outLine.polarAngle, r);
        }
        return std::make_pair(inLine, outLine);
    }
public:
    static int solve (std::vector <Point>& p, const double r) {
        int ans = 0;
        for (auto i : p) {
            int temNumber = 0;
            Circle circleI = Circle(i, r);
            std::vector <Scanline> lines;

            for (auto j : p) {
                Circle circleJ = Circle(j, r);
                if ( circleI.apart(circleJ) ) continue; // Two circles apart
                std::pair <Scanline, Scanline> pairLine = getScanline(circleI, circleJ);
                lines.push_back(pairLine.first);
                lines.push_back(pairLine.second);
            }
            if (lines.size() / 2 < ans) continue; // prune
            std::sort(lines.begin(), lines.end());
            for (auto k : lines) {
                temNumber += k.value;
                if (temNumber > ans) {
                    ans = temNumber;
                }
            }
        }
        return ans;
    }
};

int main() {
    int n;
    double r;
    Point p;
    std::vector< Point > points;
    cin >> n >> r;
    for (int i = 0; i < n; i++) {
        cin >> p.x >> p.y;
        points.push_back(p);
    }
    cout << resolvent::solve(points, r) << endl;
    return 0;
}

---

思路三：精度生成圆 (来自ZJF大佬 博客链接) 时间复杂程度：O(n * r²/eps²)

优点：更小地依赖点的个数

缺点：比较依赖于圆的半径、精度eps

思路：

以每个点为中心建立一个长为2r的正方形，从正方形的顶点开始每隔eps距离生成一个圆心，判断以该点为圆心半径为r的圆覆盖的点个数，选取其中最大覆盖点的个数的圆