[待补充][基础算法]无环有向图遍历 点价值最大问题

给定题目：

有向图G(v,e)有n个点与m个边，保证全联通且无环（无强连通分量）。

每个点（1~n）拥有一个价值Val，求所有 从 任意一个点 到 另一个点 所遍历 所有点的价值的和 中的最大值。(所有...中的...)

一、拓扑排序+DP

待补充

二、直接DP

这类图必定可以转化为树的结构，如类似于下面这个图

 

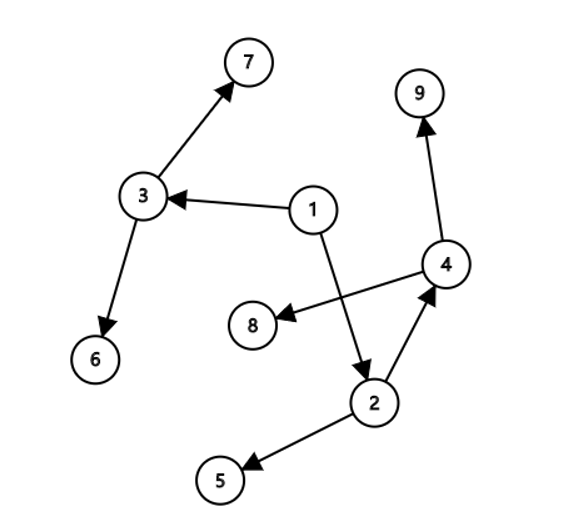
 可以转化为

 

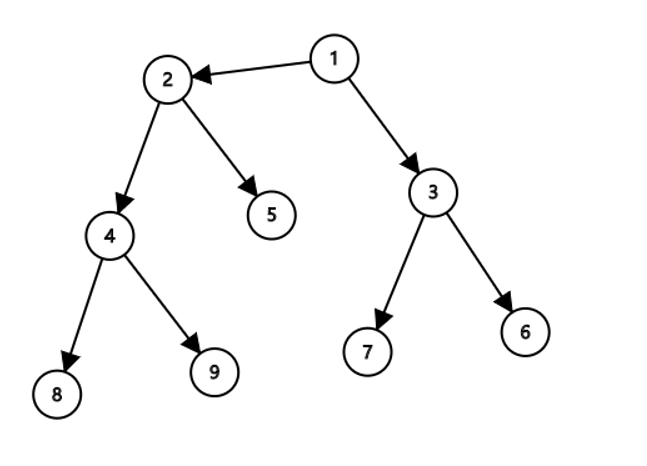
那么我们从每一深度来，设u为当前的点，vi为u的第i个儿子，基本dp递推公式就为

dp[u] = max(dp[vi]) + val[u]

其中base case为叶节点 dp[u] = val[u]

那么就可以从根节点dfs到叶节点，然后回溯每次进行判断

dp[u] = max(dp[v] + val[u] , dp[u])

那么怎么找到根节点，很明显根节点的入度为0，叶节点出度为0

那么在建边的时候记录每一个点的入度即可，再循环从1到n找到根节点

出度不需要记录，因为很明显叶节点可以直接head[u] = 0跳过前向星的查边，那么就需要把所有的点进行初始化 dp[u] = val[u]