[待补充][进阶数据结构/图论]网络流(Network-flows)
一、基本定义 有向图G = (V,E,F)中
1、边e(u,v)
① 具有固定价值c(u,v),称为最大流量,也可以称为容量,指这条边最多可以运输c(u,v)点价值;
② 具有非固定价值f(u,v),称为当前流量,其中理论上应该遵守流量限制(Capacity Constraints):
0<= f(u,v) <= c(u,v)
③ 斜对称性(Skew Symmetry): 对于同一条边e(u,v),有:
f(u,v) = -f(v,u)
这一点对于理解残留网络以及增广路非常重要!
2、点(vertex)
①流量守恒 (Flow Conservation):对于非源点、汇点,应该保证所连入边总流量 = 出边总流量,按该点为x,入边的起点为u,出边的终点为v,则公式为
∑f(u,x) = ∑f(x,v)
也可以理解为净流量(Net Flow) ∑f(u,v) = 0 其中u为该点,v为与u连接的所有点(包括入u点边的起点)
②具有两个特殊点:源点s(Source),汇点t(Toghter)。
一般来讲,∑f(u,s) = 0,∑f(t,v) = 0,也就是无法流入汇点,无法流出源点,所以 ∑f(s,v)与 ∑f(u,t)可以为任意值,但这两值相等 即
∑f(s,v) = ∑f(u,t)
注意一点,由于其他的点都得保证流量守恒,所以最大流中与源点s相连接的边的流量f(s,v)并非完全等于c(s,v),要根据不同路径而定。
3、可行流
指从源点s 到 t的所有边都保证 0 <= f(u,v) <=c(u,v),则称这该网络流为可行流。
其中,零流(所有f(u,v) = 0)属于一种可行流
4、流量值
指流出源点s 或者 流入汇点t 的总值,用单个 f 来表示
f = f(s,v) = f(u,v)
其中,保证所有流为可行流时,f的最大值称为最大流
5、一些性质
① 最大流与最短路的区别:最大流可以是多条路径从s流向t,且一条路径中的边权值并非累加,而是互相限制。
而最短路是一条路径从起点走向终点中所有经历的边的 权值 累加。
②、很明显在最大流中,从s到t的一种路径中的流量受到该路径的最小容量边的限制,且该最小容量的边的流量等于该容量,即
min_f(u,v) = min_c(u,v)
若该路径为链状(没有支路),则所有边的流量都等于最小容量边的容量。如图所示
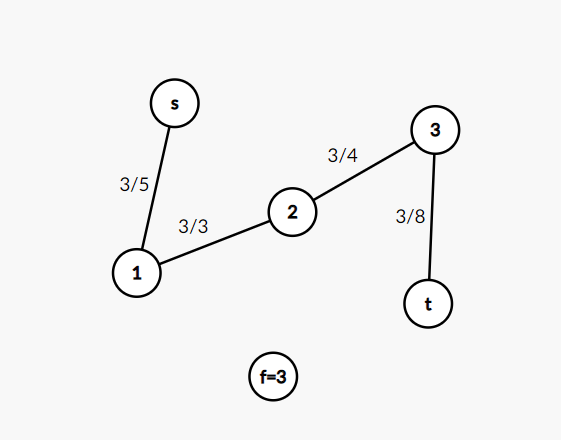
图中最小容量边为 e(1,2) ,其f(1,2) = c(1,2) = 3,且其他边 f(u,v) = c(1,2) =3
该图也可以证明最大流中与源点s相连接的边的流量f(s,v)并非完全等于c(s,v) *(注:一 2 ②)
二、残留网络(Residual Network) Gf = (V,Ef,Ff)
1、点
所有点包括源点与汇点都与原先图完全相同
残留网络的流量值为 ff
2、边
① 一方面包括剩余容量(Residual Network)
cf(u,v) = c(u,v) - f(u,v)
在增广路中指剩余的容量,也就是还没有用的容量
② 另一方面包括反向边
cf(v,u) = f(u,v)
在增广路中指对边权值选择的回溯
3、残留网络的一些性质
①、若残留网络Gf的最大流为max_ff,则在原图G中流量 f = f + max_ff 依然为可行流。
准确来说,设 0 < ff <= max_ff,f = f + ff 依然为可行流
②、若残留网络Gf的最大流 max_ff = 0,则原图G的流量值 f 为最大流
4、增广路(Augmenting Path)
在残留网络Gf中从s沿着 cf(u,v) > 0 (注意不能等于0)的边走,若可以走到t,则称这一条从s到t的路径为增广路 (针对一条路径而言)。
因此如果找不到增广路,即残留网络的最大流 max_ff = 0,则原图G的流量值为最大流。
因此只需要不断找到增广路,直到找不到则可以找到最大流。
5、增广路的一些性质
①、设此时增广路所遍历的流量为f' (并不一定等于残留网络的最大流) ,很明显该增广路中最大流 max_f' 应该等于所遍历边的最小残留容量 min_cf(u,v),即
max_f' = min_cf(u,v)
②、若残留网络没有建立反向边,则没有增广路并不代表原图是最大流,如下图所示(1为s,4为t)
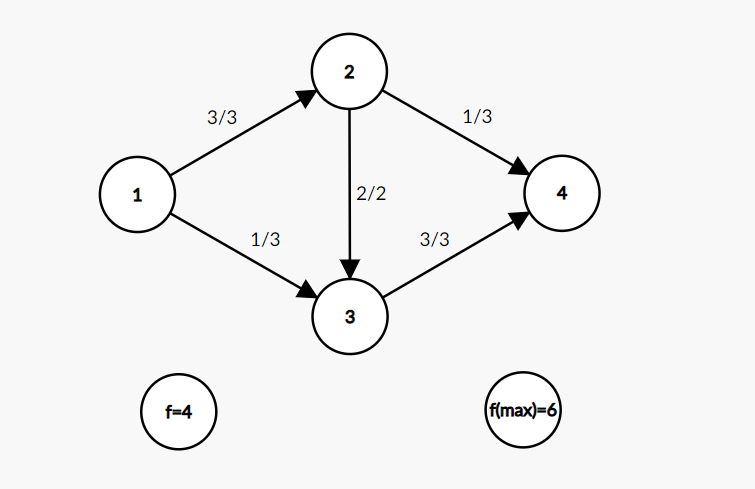
③、由于f(u,v) = -f(v,u),所以在反向边的增广路中 f(u,v) = f(u,v) + cf(v,u) = f(u,v) - cf(u,v),也就是相当于回溯。
这个操作会使这条边的流量减少,但是既然有增广路,总体流量不会减少反而增加。这条边的流量减少可以让流入其他边的流量。
也就是说,存在增广路并扩展只会让原图的流量值增加 (针对整个图而言,并非单个边),即
| f + ff | = | f | + | ff |
如上图残留网络
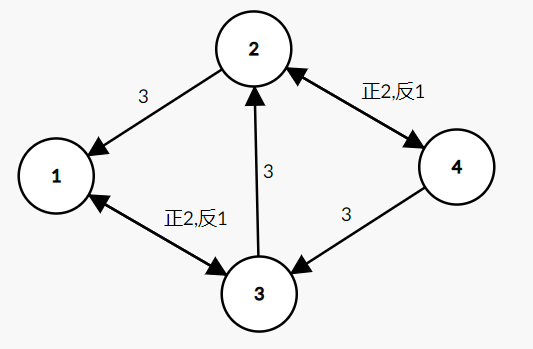
从 1 到 4 沿 cf > 0 的边走,明显 1 → 3 → 2 →4 , ff = 2,则可扩展为:
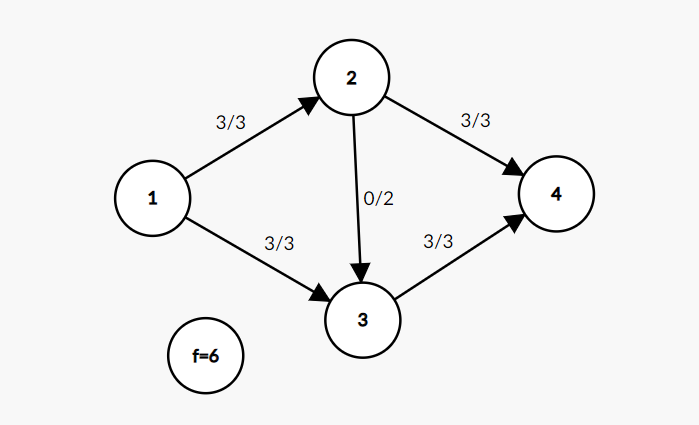
f = f + cf = 4 + 2 = 6
三、割
待补充。。
四、最大流算法
1、EK算法
基本思想:利用bfs不断寻找增广路,直到找不到。
由于寻找增广路是在残留网络中进行,所以只需要建立残留网络即可。
一些细节:
- 遍历一个点一方面判断这个点是否遍历过(val[v] = true),另一方面判断这个边的容量是否为0( !edge[i].c )
- 寻找反向边:x ^ 1结果都是成对的 如0 ^ 1 = 1,1 ^ 1 = 0,依次类推有 2和3,4和5,6和7成对...
因此从cnt = 0开始建边,cnt + 1为反向边,因此每次更新残留网络的时候用 edge[i] 减少流量, edge[i ^ 1]来增加流量表示回溯。
但是要注意前向星存边初始化 head[u] = -1而不是0,此时可以用 ~i 来判断是否为 -1 ( ~i = -(i - 1),也就是说 ~(-1) = 0)
- 在结束bfs的时候,queue并不一定为empty,若为结束后empty则不存在增广路。(此时可以定义bfs为bool型,遍历到t返回true,到empty都遍历不到就返回false)
另外bfs需要记录点是否已经遍历(boolen数组val),下次bfs要重新记录是否已经遍历来重新寻找增广路
也就是说每次bfs要注意初始化 val 与 queue
若queue不初始化会死循环;若val不初始化增广路会找不全。
- 每次寻找增广路同时需要寻找增广路的最大流量值,每个点记录到达该点的最小边容量值,公式为 les[v] = min(c[edge[i].c],les[u]),只需要初始化 les[s] = INF即可。最后 les[t] = max_f',即增广路的最大流量。
- 每次遍历到一个点需要记录到达这个点的边,用pre[u]表示,然后从 t → s开始更改边与反向边的容量,此时找到这个边的起点一方面可以在建边的时候记录起点,另一边可以利用建立的反向边( i^1 为反向边)
Code:
1 #include<bits/stdc++.h>
2 using namespace std;
3 #define ll long long
4 #define gc(a) a=getchar()
5 #define pc(a) putchar(a)
6 ll read(){
7 char c;ll x=0;bool flag=0;gc(c);
8 while(c<'0'||c>'9'){if(c=='-') flag=1;gc(c);}
9 while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48),gc(c);}
10 return flag?-x:x;
11 }
12 void pr(ll x){
13 if(x<0){x=-x;pc('-');}
14 if(x>9) pr(x/10);
15 pc(x%10+48);
16 }
17 //------------快读-----------
18 const int maxn = 2050;
19 const int maxm = 10050;
20 const int INF = 2147483647;
21 long long ans = 0,les[maxn];
22 int cnt = -1; //从-1开始建边
23 int head[maxn];
24 int s,t,n,m; //源点,汇点,点个数,边个数
25 int pre[maxn]; //前驱边
26 bool vis[maxn]; //记录点是否在队列中
27 queue<int> que;
28
29 struct Edge{ //建立残留网络
30 int v,nex;
31 long long c;
32
33 Edge(){
34 this->v = 0;
35 this->nex = -1;
36 this->c = 0;
37 }
38 Edge(int v,int nex,long long c):
39 v(v),nex(nex),c(c){}
40 }edge[maxm * 2];
41
42 void edgepush(int u,int v,long long c){
43 edge[++cnt] = Edge(v,head[u],c); //残留容量等于初始容量
44 head[u] = cnt;
45 edge[++cnt] = Edge(u,head[v],0); //反向边容量等于0
46 head[v] = cnt;
47 }
48
49 bool bfs(){
50 int u,v;
51 for(int i = 1;i <= n;i++)
52 vis[i] = 0;
53 while(!que.empty()) que.pop(); //队列以及vis初始化
54 que.push(s); //从源点开始
55 les[s] = INF;
56 vis[s] = 1;
57 while(!que.empty()){
58 u = que.front();
59 que.pop();
60 for(int i = head[u]; ~i ;i = edge[i].nex){ //遍历与u相连的边
61 v = edge[i].v;
62 if(vis[v] || !edge[i].c) continue; //两个都非常重要!
63 pre[v] = i; //记录前驱边
64 les[v] = min(les[u],edge[i].c); //更新增广路流量
65 if(v == t) return 1; //如果到达汇点,说明存在增广路
66 que.push(v); //压入队列,这俩写在if(v == t)上面下面都一样
67 vis[v] = 1;
68 }
69 }
70 return 0;
71 }
72
73 void EK(){
74 while(bfs()){ //bfs返回1则存在增广路
75 int ite = 0;
76 ans += les[t]; // 流量只加不减
77 for(int i = t;i != s;i = edge[pre[i]^1].v){ //pre[i]^1为该边的反向边
78 ite = pre[i];
79 edge[ite].c -= les[t];
80 edge[ite^1].c += les[t];
81 }
82 }
83 }
84 int main(){
85 int u,v;
86 long long c;
87 n = read(),m = read(),
88 s = read(),t = read();
89 for(int i = 1;i <= n;i++)
90 head[i] = -1;
91 for(int i = 0;i < m;i++){
92 u = read(),
93 v = read(),
94 c = read();
95 edgepush(u,v,c);
96 }
97 EK();
98 pr(ans);
99 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号