参考：贝塞尔曲线初探    http://www.cnblogs.com/jay-dong/archive/2012/09/26/2704188.html

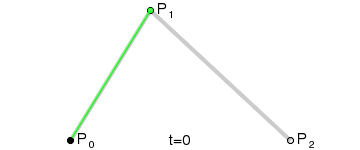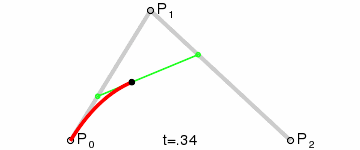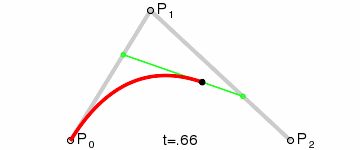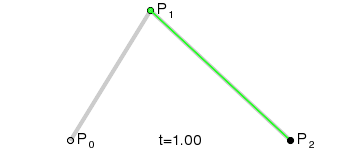
二阶贝塞尔曲线：

三阶贝塞尔曲线：

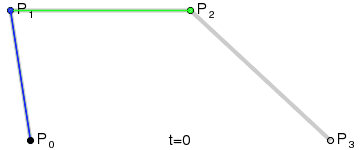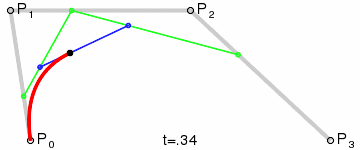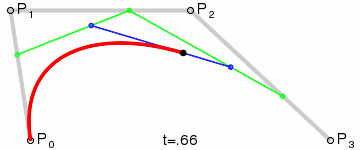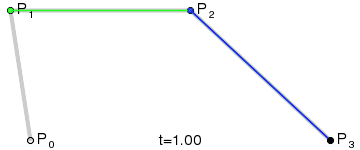
N阶贝塞尔曲线：

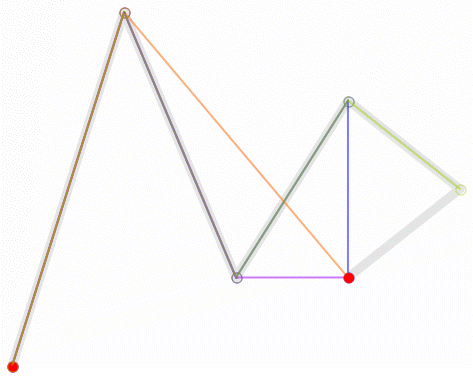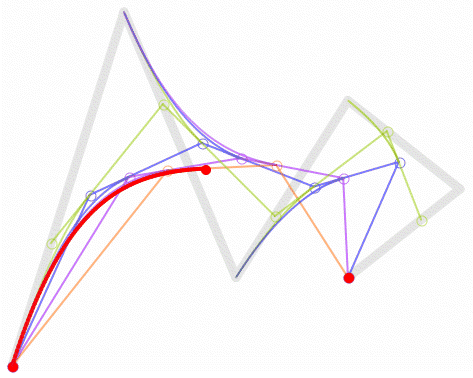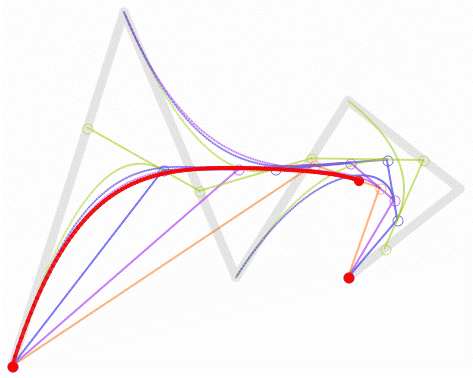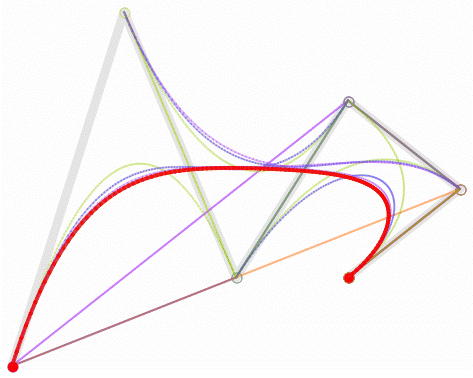
利用插值公式 p = p0 + (p1 - p0) * f 和递归运算，计算出曲线的控制点，通过连续的插值系数f的值( 取值范围[0,1] )，获得连续的曲线控制点，形成一条曲线。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class BezierLine : MonoBehaviour
{
    [SerializeField] LineRenderer lineRenderer;
    [SerializeField] int bezierPointCount = 10;
    [SerializeField] List<Vector3> pointList;

    void Start()
    {
        //显示曲线
        lineRenderer.positionCount = bezierPointCount;
        lineRenderer.SetPositions(DrawBezierLine(pointList, bezierPointCount));
    }

    public Vector3[] DrawBezierLine(List<Vector3> targetPointList, int bezierPointCount)
    {
        if (targetPointList == null || targetPointList.Count < 2 || bezierPointCount < 2)
            return null;

        Vector3[] bezierPoints = new Vector3[bezierPointCount];

        for (int i = 0; i < bezierPointCount; i++)
        {
            //通过递增的插值系数f(保证取值范围0~1), 获取连续的曲线折点
            bezierPoints[i] = BezierPoint(1.0f * i / (bezierPointCount - 1), targetPointList);
        }
        return bezierPoints;
    }

    //一阶直线(插值系数, 起始点, 终止点)
    Vector3 BezierPoint(float f,Vector3 p0, Vector3 p1)
    {
        插值计算原始公式, 插值系数: f >= 0 & f <= 1
        //return p0 + (p1 - p0) * f;
        //公式变形
        return (1 - f) * p0 + f * p1;
    }


    //二阶曲线(插值系数, 起始点, 控制点, 终止点)
    Vector3 BezierPoint(float f,Vector3 p0, Vector3 p1, Vector3 p2)
    {
        降为一阶
        //Vector3 p0p1 = (1 - f) * p0 + f * p1;
        //Vector3 p1p2 = (1 - f) * p1 + f * p2;
        //return (1 - f) * p0p1 + f * p1p2;
        //合并化简公式
        return Mathf.Pow(1 - f, 2) * p0 + 2 * f * (1 - f) * p1 + Mathf.Pow(f, 2) * p2;
    }

    //三阶曲线(插值系数, 起始点, 控制点, 控制点, 终止点)
    Vector3 BezierPoint(float f,Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
    {
        降为二阶
        //Vector3 p0p1 = (1 - f) * p0 + f * p1;
        //Vector3 p1p2 = (1 - f) * p1 + f * p2;
        //Vector3 p2p3 = (1 - f) * p2 + f * p3;
        降为一阶
        //Vector3 p0p1p2 = (1 - f) * p0p1 + f * p1p2;
        //Vector3 p1p2p3 = (1 - f) * p1p2 + f * p2p3;
        //return (1 - f) * p0p1p2 + f * p1p2p3;
        //合并化简公式
        return Mathf.Pow(1 - f, 3) * p0 + 3 * f * Mathf.Pow(1 - f, 2) * p1 + 3 * Mathf.Pow(f, 2) * (1 - f) * p2 + Mathf.Pow(f, 3) * p3;
    }

    //N阶曲线(插值系数, List(起始点, 控制点 ··· , 终止点))
    public Vector3 BezierPoint(float f, List<Vector3> pointList)
    {
        if (pointList.Count == 1)
            return pointList[0];
        //降阶
        List<Vector3> newPointList = new List<Vector3>();
        for (int i = 0; i < pointList.Count - 1; i++)
        {
            newPointList.Add((1 - f) * pointList[i] + f * pointList[i + 1]);
        }
        //递归计算
        return BezierPoint(f, newPointList);
    }

}